Hvor mange diametre har en omkrets?

En omkrets har uendelige diametre. Det er lett å se at det er slik, hvis det er basert på definisjonen av diameter, som er segmentet som passerer samtidig gjennom sentrum av omkretsen og med to punkter av det samme.

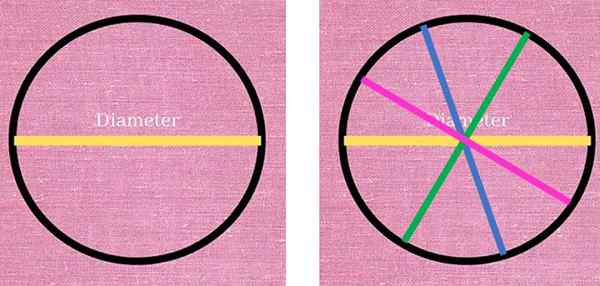
I den følgende figuren, til venstre, observeres den gule linjen som tilsvarer en diameter på omkretsen og delt i to deler. På høyre side ble tre andre diametre tegnet i forskjellige farger: blå, grønn og rosa. Alle har samme lengde og tilfredsstiller betingelsen for å slå sammen to punkter i omkretsen, gjennom midten av det samme.

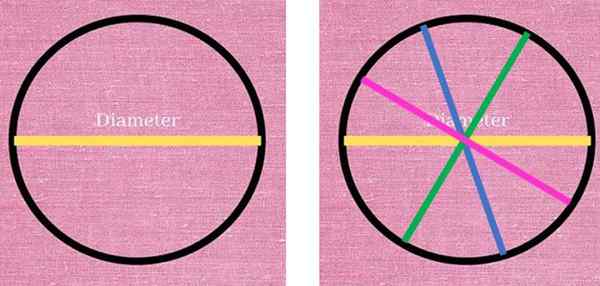Diameteren er et særegent segment, som alltid går gjennom sentrum av omkretsen og sammen med to punkter i dette. På venstre deler den gule diameteren omkretsen i to. Til høyre er det andre diametre som også deler omkretsen i to halvdeler. Kilde: f. Zapata.

Som det kan sees, er mulighetene for å trekke diametre uendelige, da uendelige er punktene som danner omkretsen. Det samme kan bekreftes om radiusen, som er segmentet som forener et hvilket som helst punkt i omkretsen med sentrum: et uendelig antall radioer kan trekkes.

Og når du plasserer to motsatte radioer fra hverandre, oppnås en diameter, fordi radius måler halvparten av dette.

Diameter, radio og omkretslengde

Det være seg diameteren på enhver omkrets og r, dens radius. Når diameteren måler dobbelt så mye som radioen, kan det skrives:

D = 2 ∙ r

Det betyr at hvis radius for en sirkel for eksempel er r = 5 cm, er diameteren på den d = 2 ∙ 5 cm = 10 cm.

Det kan tjene deg: Fibonacci -serien: egenskaper, naturlige forhold, applikasjoner

Diameteren er også kjent som Major tau. Strengene er linjer eller segmenter som er trukket mellom to punkter i omkretsen, men som ikke nødvendigvis går gjennom sentrum. Bare diameteren har den skillet.

I den følgende figuren kan du se forskjellen og se hvorfor diameteren (rød) faktisk er den største av strengene som kan trekkes på omkretsen:

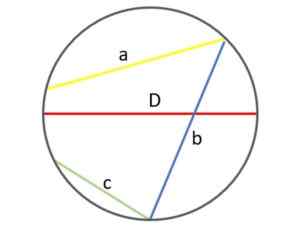Forskjellige tau i en omkrets: diameteren er den største av alle. Kilde: f. Zapata.

Selvfølgelig er diametermålet (og derfor radius) den samme i en gitt omkrets. Når det varierende, oppnås en mindre eller større omkrets, ifølge.

På den annen side varierer størrelsen på strengene i samme omkrets, avhengig av hvor langt eller nær punktene er punktene som blir med. I eksemplet som er vist, er det grønne “C” -tauet tilsynelatende kortere enn “A” og “B” -strengene.

Og antallet strenger som kan trekkes er også uendelig.

Omkretsen av omkretsen

For sin del tilsvarer omkretsens lengde. Det er relatert til dens diameter, siden jo høyere dette er, jo større er omkretsen (omkretsen er større).

Forholdet eller kvotienten mellom omkrets og diameter er en konstant kalt π (lyder "Pi"). Verdien av π er 3.141592 ... Suspensive punkter indikerer at mengden desimaler og uendelig, noe som er fordi Pi er et irrasjonelt tall. For praktiske formål kan PI imidlertid ganske enkelt runde opp 3.14

Kan tjene deg: Hvor mye må du legge til 3/4 for å få 6/7?

Hvis omkretsen er betegnet som C og diameteren som D, blir denne grunnen hevet som følger:

C / d = π

Derfor er formelen for omkretsens lengde:

C = π ∙ D

Eller hvis foretrukket basert på radius r:

C = 2π ∙ r

Illustrerende eksempel

Bildet viser tre identiske omkretser, utpekt med bokstaver A, B og C. I hver og en kjører mauren veien på de blå fargesegmentene, for å gå fra ett punkt til et annet av omkretsen.

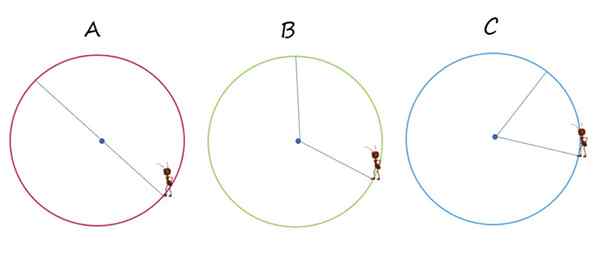Myren beveger seg fra ett punkt til et annet av omkretsen gjennom de tynneste blå linjene. Kilde: f. Zapata.

1.- I hvilke av tilfellene forekommer forskyvningen nøyaktig på omkretsens diameter?

Svar

Bare i tilfelle A, fordi den veien går gjennom sentrum av omkretsen og går fra ett punkt til et annet av det samme.

2.- Hvor mange radioer insektet reiser i hvert tilfelle?

Svar

I noen av de tre tilfellene reiser myren to radioer i omkretsen.

3.- Hvilken av stiene tilsvarer størst avstand?

Svar

Reisen er like lang i hvert tilfelle, tilsvarer to radioer i omkretsen.

4.- I hvilket tilfelle mauren er lenger borte fra utgangspunktet?

Svar

I tilfelle A, siden det er på det punktet som er nettopp foran det, er myren i de resterende nærmere utgangspunktet.

5.- Og i hvilket tilfelle avslutter mauren at ruten er nærmere opprinnelsesstedet?

Kan tjene deg: tegn på gruppering

Svar

I tilfelle c.

6.- Hvis omkretsens radius er 20 cm, hvor mange centimeter gjør hvert rutemål?

Svar

Siden mauren går en avstand lik to radioer, er den totale tilbakelagte avstanden 40 cm.

Løste øvelser

Oppgave 1

Beregn radius for en sirkel hvis diameter er 4.5m.

Løsning

Radioen er halvparten av diameteren, hvis dette måler 4.5 cm, da er radio r 2.25 cm.

Oppgave 2

Finn omkretsen av omkretsen av trening 1.

Løsning

Omkretsen beregnes gjennom diameteren eller gjennom radius, som foretrukket. I det første tilfellet:

C = π ∙ D

Forutsatt at π = 3.14 til runde gir erstatning av verdier følgende resultat:

C = π ∙ d = 3.14 ∙ 4.5 cm = 14.13 cm

Øvelse 3

En designer blir bedt om å tegne en hjerteformet logo, med dimensjonene angitt på figuren. De buede delene tilsvarer eksakte halvsirkler.

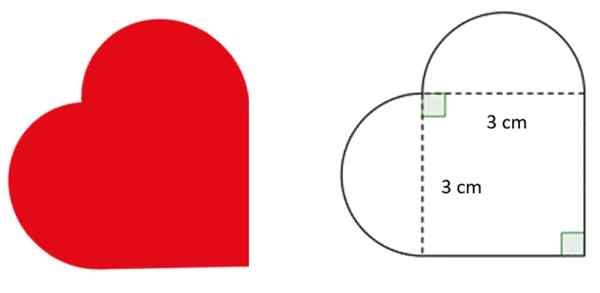
Med dette informasjonen svar:

1. Hva er radiusen til semi-sirkunene?
2. Hvor mye er hjertets omkrets?

Løsning på

Diameteren på halvirkuferansene tilsvarer siden av torget, som er 3 cm. Derfor måler radius, som er halvparten, 1.5 cm.

Løsning b

Omkretsen av den hjerteformet figuren er summen av de to ytre sidene av torget og omkretsen av semi -samsvarene. Som identisk er dets omkrets tilsvarer en komplett sirkel med diameter 3 cm:

C = π ∙ d = 3.14 ∙ 3 cm = 9.42 cm

Derfor er omkretsen P på figuren:

P = 9.42 cm + 3 cm + 3 cm = 15.42 cm