Vanlige, uregelmessige desagon, egenskaper, eksempler

Han Decagon Det er en flat figur med en polygon -formet på 10 sider og 10 hjørner eller tips. Dekagonene kan være regelmessige eller uregelmessige, i det første tilfellet har alle sider og indre vinkler samme mål, mens sidene og/eller vinklene i det andre er forskjellige fra hverandre fra hverandre.

Figur 1 viser eksempler på dekagoner av hver type, og som vi kan se er den vanlige desagon veldig symmetrisk.

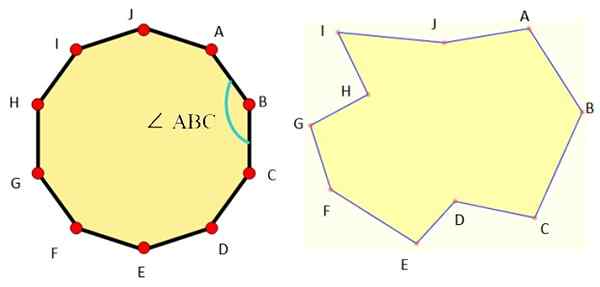Figur 1. Til venstre en vanlig desagon og til høyre en uregelmessig desagon. Kilde: Wikimedia Commons/F. Zapata/Mathpenref.

De grunnleggende elementene i alle desagon er:

-Sider, linjesegmentene som når du blir med på desagon.

-Hjørner, eller peker mellom hver påfølgende side.

-Innvendige og ytre vinkler mellom tilstøtende sider.

-Diagonaler, segmenter som forener to ikke -samtykke vertekser.

Hjørnene kalles med store bokstaver, som vist i figur 1, der de første bokstavene i alfabetet ble brukt, men alle bokstaver kan brukes.

Sidene er symbolisert med de to bokstavene i toppunktene blant dem, for eksempel AB -siden er den mellom toppunktene A og B. På samme måte er det gjort med diagonalene, så vi har diagonal AF, som blir med på poeng A og F.

For vinkler bruker vi dette symbolet: ∠, lik en skrå L. For eksempel er vinkelen ∠ ABC en hvis toppunkt er B og hvis sider er AB- og BC -segmentene.

[TOC]

Vanlig desagon

I den vanlige desagon har alle sider samme mål, så vel som indre vinkler. Derfor sies det å være likesid (like sider) og like (Like vinkler). Det er en veldig symmetrisk figur

Interiørvinkler til en vanlig desagon

For å finne målet på de indre vinklene til en vanlig polygon, inkludert den vanlige desagon, brukes følgende formel:

Hvor:

-Jeg er målet på vinkelen i grader.

-n er antall sider av polygonen. I tilfelle av Decagon n = 10.

Kan tjene deg: heptagon

Erstatning n = 10 I den forrige formelen får vi følgende:

Nå sies det at en polygon er konveks Hvis det er vinkelmål er mindre enn 180 º, ellers er polygonen konkav. Som enhver indre vinkel på den vanlige desagon måler 144º og er mindre enn 180 º, er det en konveks polygon.

Sum av interne vinkler

Summen av målene for de interne vinklene til en hvilken som helst polygon er i grader:

S = (n-2) x 180º; n er alltid større enn 2

I denne formelen må vi:

-S er summen av målene for de indre vinklene.

-n er antall sider. For desagon n = 10

Bruke formelen for n = 10 resultater:

S = (10 - 2) x 180º = 1440º

Utvendige vinkler 

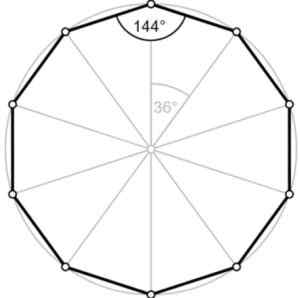
En ytre vinkel dannes mellom den ene siden og forlengelsen av den tilstøtende siden, la oss se:

Figur 2.- Den ytre vinkelen til den vanlige desagon måler 36º. Fontene. Wikimedia Commons/f. Zapata.

Vinkelen ∠ ABC pluss den ytre vinkelen legger til 180º, det vil si de er Tillegg. Derfor er den ytre vinkelen lik 180º-144º = 36º, som vi ser på figuren.

Antall diagonaler

Som nevnt før, er diagonalene segmentene som forener ikke -samtykke Vertices. Hvor mange diagonaler kan vi spore i en desagon? Når antall hjørner er lite, kan de enkelt telles, men når antallet øker kan du miste kontoen.

Heldigvis er det en formel for å vite antall diagonaler som en polygon har n sider:

For desagon erstatter vi n = 10 og får:

D = 10 x (10 - 3) /2 = 35

I den vanlige desagonen kuttes alle diagonaler på et tidspunkt, som er midten av figuren:

Figur 3. Vinkler og diagonaler av den vanlige desagon. Kilde: Wikimedia Commons.

Senter

Sentrum av en polygon er definert som det like store punktet i ethvert toppunkt. I forrige figur sammenfaller senteret med skjæringspunktet for alle diagonaler.

Omkrets

Hvis den vanlige desagonen har side A, er omkretsen P summen av alle sider:

Kan tjene deg: 90 Divisors: Hva er og forklaring

P = 10.til

Område

Å vite lengden til På siden beregnes det vanlige dekagonområdet av:

En omtrentlig formel for området er:

Og et tredje alternativ for å finne området er etter lengden på apothem l_TIL. Dette er segmentet som blir med midtpunktet på den ene siden med midten av polygonen.

I dette tilfellet kan området beregnes ved å bruke formelen:

Uregelmessig desagon

Den uregelmessige desagon er ikke likesid eller ekvista, og generelt mangler den symmetrien til den vanlige figuren, selv om noen desagoner kan ha symmetri -akse.

De kan også være konvekse eller konkave, hvis det er indre vinkler større enn 180º.

Den uregelmessige desagon i figur 1 er konkav, siden noen av dens indre vinkler er større enn 180º. Det er tydelig at det er mange kombinasjoner av vinkler og sider som gir opphav til en uregelmessig desagon.

I alle fall er det oppfylt at:

-De indre vinklene til en uregelmessig desagon tilfører også 1440º.

-Den har også 35 diagonaler.

Område av en uregelmessig desagon av Gauss Determinants

Generelt er det ingen unik formel for å finne området til en uregelmessig polygon, siden sidene og vinklene er forskjellige. Du kan imidlertid finne å kjenne koordinatene til toppunktene og beregne Gauss Determinants:

-La oss ringe (x_n , og_n ) til koordinatene til toppunktene, med n varierende fra 1 til 10.

-Du kan starte fra et hvilket som helst toppunkt, som koordinater vil bli tildelt (x x₁, og₁ ). Nå må du erstatte verdiene for hver koordinat i denne formelen:

Hvor determinanter er nettopp operasjonene mellom parenteser.

-Det er viktig å merke seg at den siste determinanten involverer den første toppunktet sammen med den siste. For Decagon ville det være slik:

(x₁₀og₁ - x₁og₁₀)

Kan tjene deg: LaGrange interpolasjon

Viktig: Barene er de med absolutt verdi og betyr at det endelige resultatet alltid er med et positivt tegn.

Prosedyren kan være arbeidskrevende når figuren har mange hjørner, i tilfelle av desagon er det 10 operasjoner, så det anbefales å lage en tabell eller en liste.

Trening løst

Beregn det uregelmessige desagonområdet vist på figuren. Koordinatene til toppunktene er a, b, c ... j, hvis verdier er vist til venstre.

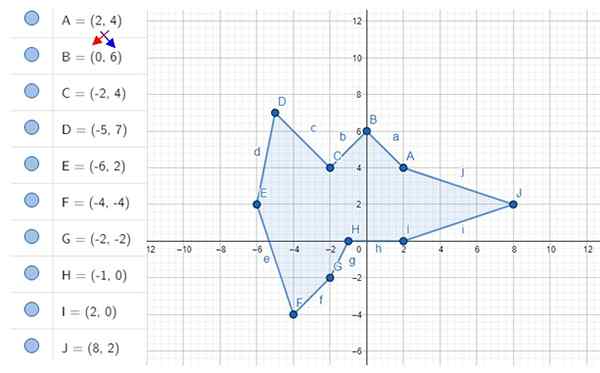Figur 4. Uregelmessig desagon og dens toppunkter. Kilde: f. Zapata med Geogebra.

Løsning

-Vi gjør hver av de 10 operasjonene:

• 2 × 6 - 4 × 0 = 12 - 0 = 12
• 0 × 4 - 6 × (-2) = 0 + 12 = 12
• (-2) × 7- 4 × (-5) = -14 + 20 = 6
• (-5) × 2 -7 × (-6) = -10 + 42 = 32
• (-6) × (-4) -2 × (-4) = 24 + 8 = 32
• (-4) × (-2)-(-4) × (-2) = 8-8 = 0
• (-2) × 0-(-2) × (-1) = 0 -2
• (-1) × 0 - 0 × (2) = 0 - 0 = 0
• 2 × 2 - 0 × 8 = 4 - 0 = 4
• 8 × 4 -2 × 2 = 32 - 4 = 28

-Vi legger til resultatene:

12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124

Et positivt resultat oppnås selv uten stolper med absolutt verdi, men hvis det er negativt, endres det samme.

-Det forrige resultatet er delt med 2, og det er polygonområdet:

A = 124/2 = 62

Decangon -egenskaper

Nedenfor er sammendraget av de generelle egenskapene til en desagon, enten det er regelmessig eller uregelmessig:

-Har 10 sider og 10 hjørner.

-Summen av interne vinkler er 1440º.

-Det er 35 diagonaler.

-Omkretsen er summen av alle sider.

-Du kan lage trekanter inne i et polygon -tegningssegmenter fra et toppunkt til alle andre. I en desagon er det mulig å tegne 8 trekanter på denne måten, som vist nedenfor:

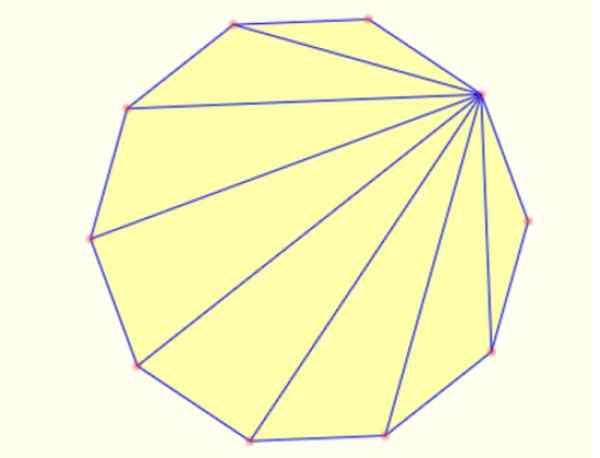Figur 5. Interne trekanter i en vanlig desagon. Kilde: Mathpenref.

Referanser

1. Alexander, d. 2013. Geometri. 5. plass. Utgave. Cengage Learning.
2. Decagon.com. Decagon. Gjenopprettet fra: Decagon.com
3. Matematikk åpen referanse. Decagon. Gjenopprettet fra: Mathpenref.com.
4. Sangaku Maths. Elementer av en polygon og dens klassifisering. Gjenopprettet fra: sangakoo.com.
5. Wikipedia. Decagon. Gjenopprettet fra: er.Wikipedia.com.