Implisitte derivater hvordan de løses og løste øvelser

De Implisitte derivater De er verktøy som brukes i en differensieringsteknikk som brukes på funksjoner. De gjelder når det ikke er mulig, under regelmessige metoder, utfører klarering av den avhengige variabelen som skal utlede. Denne klaring gjøres basert på den uavhengige variabelen.

For eksempel i uttrykket 3xy³ - 2y + xy² = xy, du kan ikke få uttrykket som definerer "y" avhengig av "x". Slik at når det differensielle uttrykket DY/DX kan oppnås.

[TOC]

Hvordan løses implisitte derivater?

For å løse en implikasjon er det basert på et implisitt uttrykk. For eksempel: 3xy³ - 2y + xy² - Xy = 0. Dette er allerede klart klarert, men for å gjøre det er ikke en nødvendig betingelse for å oppnå derivatet Y angående x. Deretter er hvert av elementene avledet og respekterer kjedestyret for blandede funksjoner:

3xy³ Den består av 2 variabler, derfor d (3xy³) Det vil bli behandlet som derivatet av et produkt av funksjoner.

D (3xy³)/dx = 3y³ + 3y².(3x) og '= 3y³ + 9xy² og'

Der elementet og 'er kjent som "og fetter”Og dy/dx representerer

-2y stammer i henhold til lov k.U = k.ELLER'

D (-2y) = -2 og '

Xy² antar at en annen differensial sammensatt av et produkt av funksjoner

D (xy²) = y² + 2xy og '

-XY er en homolog måte

d (-xy) = -y -x og '

De erstattes i likhet, vel vitende om at null derivat er null.

3y³ + 9xy² og ' - 2 og' + og² + 2xy og ' - y - x og' = 0

Elementene som har begrepet og 'er gruppert sammen på den ene siden av likhet

Kan tjene deg: colineale vektorer

3y³ + og² - y = -9xy² og ' + 2 og' + x og '

Den vanlige faktoren og 'i riktig medlem av likestilling blir trukket ut

3y³ + og² - y = y '(-9xy² + x + 2)

Til slutt, begrepet som multipliserer og '. Dermed oppnå uttrykket som tilsvarer det implisitte derivatet av y angående x.

og '= dy/dx = (3y³ + og² - y)/(-9xy² + x + 2)

Kjedestyre

I den implisitte avledningen respekteres alltid kjedestyret. Alle differensielle uttrykk vil bli gitt avhengig av den uavhengige variabelen x. Slik at enhver variabel θ forskjellig fra x må omfatte begrepet dθ/dx etter å ha blitt avledet.

Dette begrepet vil bare vises i første grad eller med eksponenten lik 1. Denne kvaliteten gjør det helt klart under tradisjonelle faktoriseringsmetoder. Slik at det blir mulig å oppnå uttrykket som definerer differensialet Dθ/dx.

I kjedestyret vises den progressive naturen til differensiering eller derivatprosess. Hvor for enhver sammensatt funksjon f [g (x)], må differensialuttrykket av f være

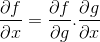
Operativ ordre

I hver formel eller avledningslov som brukes, må rekkefølgen på variablene tas i betraktning. Kriteriene knyttet til den uavhengige variabelen blir respektert, uten å endre dens korrelasjon med den avhengige variabelen.

Forholdet mellom den avhengige variabelen på tidspunktet for avledet tas direkte.; Med unntak av at dette vil bli betraktet som en annen funksjon, og det er grunnen til at kjeden Regelkriterier for blandede funksjoner blir brukt.

Dette kan utvikles i uttrykk med mer enn 2 variabler. Under de samme prinsippene vil alle differensialer som refererer til avhengige variabler bli betegnet.

Kan tjene deg: Hva er retningslinjen? (Geometri)

Grafisk håndteres de samme kriteriene som definerer derivatet. Mens derivatet er skråningen til linjetangenten til kurven i planet, representerer resten av differensialene som tilhører de avhengige variablene (DY/DX, DZ/DX) tangentplan til vektorlegemene beskrevet av funksjonene til flere variabler.

Implisitt av en funksjon

Det sies at en funksjon implisitt er definert, hvis uttrykket y = f (x) kan representeres som en multippel variabel funksjon f (x, y) = 0 mens f er definert i plan r².

3xy³ - 2y + xy² = x og kan skrives i 3xy -skjemaet³ - 2y + xy² - Xy = 0

Med tanke på umuligheten av å forklare funksjonen y = f (x).

Historie

Differensialberegningen begynte å bli utnevnt av forskjellige matematiske forskere, rundt det syttende århundre. Første gang det ble nevnt var gjennom Newton og Leibnizs bidrag. Begge behandlet differensialberegningen fra forskjellige synspunkter, men konvergerte i resultatene sine.

Mens Newton fokuserte på differensiering som en hastighet eller variasjonsrate, var Leibniz -tilnærmingen mer geometrisk. Det kan sies at Newton angrep formodningene som Apollonius fra Perge og Leibniz har de geometriske ideene til Fermat.

Den implisitte avledningen vises umiddelbart når de differensielle og omfattende ligningene vurderer. De utvidet det geometriske konseptet Leibniz til r³ og til og med flerdimensjonale rom.

applikasjoner

Implisitte derivater brukes i forskjellige situasjoner. De er vanlige i valutakursproblemer mellom relaterte variabler, der, avhengig av studien, vil variablene bli ansett som avhengige eller uavhengige.

De har også interessante geometriske applikasjoner, for eksempel i problemer med refleksjoner eller skygger, på figurer hvis form kan modelleres matematisk.

Kan tjene deg: Kvoteprøvetaking: Metode, fordeler, ulemper, eksempler

De er av hyppig bruk innen økonomi og ingeniørfag, så vel som i forskjellige undersøkelser av naturfenomener og eksperimentelle bygninger.

Løste øvelser

Oppgave 1

Definer det implisitte uttrykket som definerer DY/DX

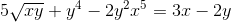
Hvert element er forskjellig fra uttrykket

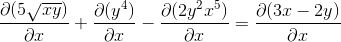
Etablere kjedestyret i hver kompetent sak

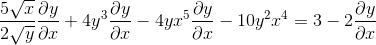
Gruppering på den ene siden av likhet elementene som har dy/dx

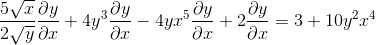
Factoring ved bruk av den vanlige faktoren

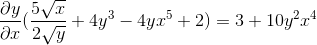
Blir ryddet ved å få det etterspurte uttrykket

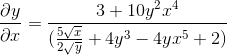
Oppgave 2

Definer det implisitte uttrykket som definerer DY/DX

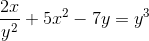
Uttrykke derivater for å utføre

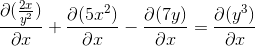
Implisitt avleder i henhold til kjedestyret

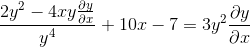
Factoring av vanlige elementer

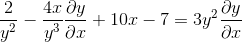
Gruppere begrepet dy/dx på den ene siden av likhet

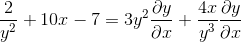
Vanlig faktor til differensialelement

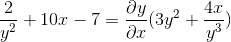
Vi fjerner og oppnår det etterspurte uttrykket

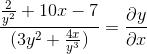
Referanser

1. Beregning av en enkelt variabel. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. nov. 2008
2. Den implisitte funksjonsteoremet: Historie, teori og applikasjoner. Steven G. Krantz, Harold R. Parker. Springer Science & Business Media, 9. nov. 2012
3. Multivariabel analyse. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. desember. 2010
4. Systemdynamikk: Modellering, simulering og kontroll av mekatroniske systemer. Dean c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. mars. 2012
5. Kalkulus: Matematikk og modellering. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1. januar. 1999