Delvis derivategenskaper, beregning, øvelser

De Delvis derivater av en funksjon med flere uavhengige variabler er de som oppnås ved å ta det vanlige derivatet i en av variablene, mens de andre opprettholdes eller tas som konstanter.

Det delvise derivatet i en av variablene, bestemmer hvordan funksjonen varierer på hvert punkt, per endringsenhet den aktuelle variabelen. 

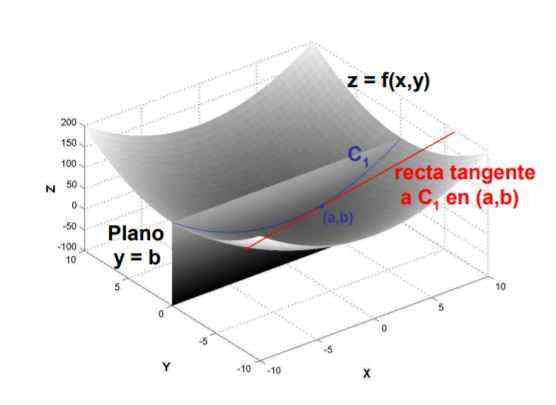Figur 1. Hellingen av tangentlinjen til kurven dannet av skjæringspunktet mellom planet y = b med overflaten f (x, y) på punktet (a, b) er det delvise derivatet av f med hensyn til x, evaluert på det punktet. Kilde: UPM.er

På grunn av definisjonen beregnes det delvise derivat.

Anta at saken om en funksjon F Det avhenger av variablene x og og, det vil si for hvert par (X, y) A er tildelt z: 

F: (x, y) → z .

Det delvise derivatet av funksjonen z = f (x, y), med respekt for x er definert som:

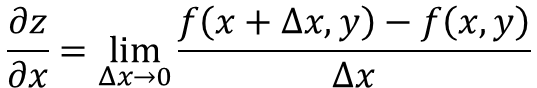
Nå er det flere måter å betegne delvis derivat av en funksjon, for eksempel:

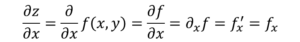
Forskjellen med det vanlige derivatet, når det gjelder notasjon, er at d av avledning endres til symbolet ∂, kjent som "Jacobi D".

[TOC]

Egenskaper til delvise derivater

Det delvise derivatet av en funksjon av flere variabler, med hensyn til en av dem, er det vanlige derivatet i nevnte variabel og vurderer resten som fast eller konstant. For å finne det delvise derivatet, kan avledningsreglene for vanlige derivater brukes.

Under hovedegenskapene:

Kan tjene deg: Vanlig faktor for gruppering av begreper: eksempler, øvelser

Kontinuitet

Hvis en funksjon f (x, y) har delvis derivater i x og og på punktet (Xo, meg) Da kan det sies at funksjonen er kontinuerlig på det tidspunktet.

Kjedestyre

En funksjon f (x, y) Med kontinuerlige delvis derivater i x og og, som igjen avhenger av en parameter t gjennom x = x (t) og y = y (t), Det har vanlig derivat med hensyn til variabelen t, som beregnes av kjedestyret:

d_t Z = ∂_xz d_tx + ∂_ogz d_tog

Lukke eller låse eiendommer

Det delvise derivatet med hensyn til en av variablene i en funksjon F av to eller flere variabler (X, y, ...), Det er en annen funksjon g I de samme variablene, for eksempel: 

G (x, y, ...) = ∂_og f (x, y, ...)

Det vil si at delvis avledning er en operasjon som går fra rⁿ a rⁿ. I den forstand sies det at det er en lukket operasjon.

Påfølgende delvis derivater

De påfølgende delvise derivater av en funksjon av flere variabler kan defineres, noe som gir opphav til nye funksjoner i de samme uavhengige variablene.

Være funksjonen f (x, y). Følgende påfølgende derivater kan defineres:

F_Xx = ∂_xF ;  F_Yy = ∂_YyF ; F_Xy = ∂_XyF og F_Yx = ∂_YxF

De to siste er kjent som Blandede derivater Fordi de involverer to forskjellige uavhengige variabler.

Schwarz teorem

Være en funksjon f (x, y), definert på en slik måte at dens delvise derivater er kontinuerlige funksjoner i en åpen undergruppe av R².

Så for hvert par (X, y) At de tilhører nevnte undergruppe, er blandede derivater identiske:

∂_XyF = ∂_YxF

Den forrige uttalelsen er kjent som Schwarz teorem.

Hvordan beregnes delvis derivater?

Delvis derivater beregnes på samme måte som vanlige funksjoner derivater i en enkelt uavhengig variabel. Når det delvise derivatet av en funksjon av flere variabler tas med hensyn til en av dem, blir de andre variablene tatt som konstanter.

Kan tjene deg: halvparten av 15

Nedenfor er flere eksempler:

Eksempel 1

Være funksjonen:

f (x, y) = -3x² + 2 (og - 3)²

Det blir bedt om å beregne det første delvise derivatet med hensyn til x og det første delvise derivatet med hensyn til og.

Fremgangsmåte

For å beregne delvis F med respekt for x, Er tatt og som konstant:

∂_xF = ∂_x(-3x² + 2 (og - 3)² ) = ∂_x(-3x² )+ ∂_x(2 (og - 3)² ) = -3 ∂_x(x²) + 0 = -6x.

Og på sin side for å beregne derivatet med hensyn til og Er tatt x som konstant:

∂_ogF = ∂_og(-3x² + 2 (og - 3)² ) = ∂_og(-3x² )+ ∂_og(2 (og - 3)² ) = 0 + 2 · 2 (y - 3) = 4y - 12.

Eksempel 2

Bestem andreordens delvise derivater:  ∂_Xxf, ∂_Yyf, ∂_YxF og ∂_XyF For samme funksjon F av eksempel 1.

Fremgangsmåte

I dette tilfellet, ettersom det første delvise derivatet allerede er beregnet i x og og (Se eksempel 1):

∂_XxF = ∂_x(∂_xf) = ∂_x(-6x) = -6

∂_YyF = ∂_og(∂_ogf) = ∂_og(4y - 12) = 4

∂_YxF = ∂_og(∂_xf) = ∂_og(-6x) = 0

∂_XyF = ∂_x(∂_ogf) = ∂_x(4y - 12) = 0

Det observeres det ∂_YxF = ∂_XyF, dermed oppfylle Schwarzs teorem, siden funksjonen F og dets første ordre delvise derivater er alle kontinuerlige funksjoner i R².

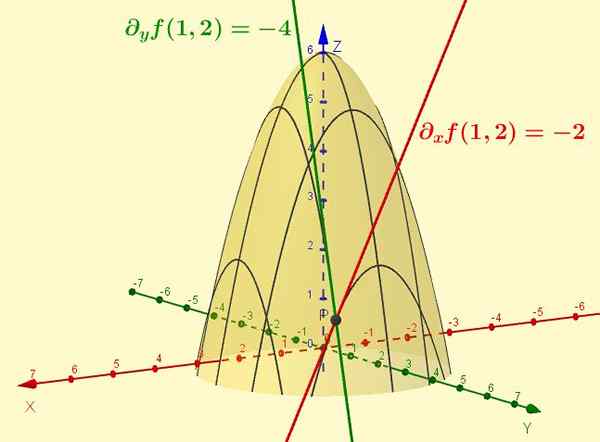
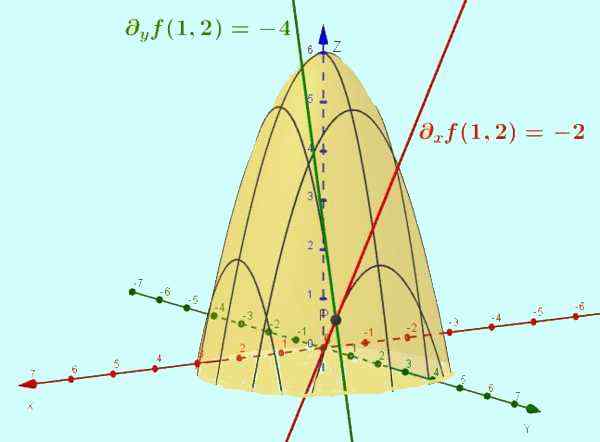Figur 2. Funksjonen z = f (x, y) = -x2 - y2 + 6 er overflaten vist på figuren. Det delvise derivatet med hensyn til x er helningen på tangentlinjen til kurven som er resultatet av skjæringspunktet mellom nevnte overflate med planet y = ctt (det spesielle tilfellet er vist y = 2). Tilsvarende delen av f med hensyn til og er skråningen til tangenten til krysset med x = 1, på punktet (1, 2, 1).

Løste øvelser

Oppgave 1

Være funksjonen:

Kan tjene deg: kvadratiske suksesser: eksempler, regel og øvelser løst

f (x, y) = -x² - og² + 6

Finn funksjoner G (x, y) = ∂_xF  og H (x, y) = ∂_ogF.

Løsning

Det delvise derivatet av F med respekt for x, som variabelen og Det blir konstant:

G (x, y) = - 2x

Tilsvarende det delvise derivatet av g med respekt for og, driver med x konstant, noe som resulterer for funksjonen h:

H (x, y) = -2y

Oppgave 2 

Evaluere for poenget (1, 2) funksjonene f (x, y) og G (x, y) av øvelse 1. Tolke resultatene.

Løsning

Verdier erstattes x = 1 og y = 2 å skaffe seg:

F (1,2) = -(1)² -(2)² + 6 = -5 + 6 = 1

Dette er verdien som tar funksjonen F når den blir evaluert på det tidspunktet.

Funksjonen f (x, y) Det er en to -dimensjonal overflate og koordinat z = f (x, y) Det er høyden på funksjonen for hvert par (X, y). Når paret er tatt (1.2), Overflatehøyden f (x, y) er Z = 1.

Funksjonen G (x, y) = - 2x representerer et plan i det tre -dimensjonale rommet hvis ligning er Z = -2x O vel -2x + 0 og -z = 0.

Nevnte fly er vinkelrett på flyet Xz Og gå gjennom punktet (0, 0, 0). Når den blir evaluert i x = 1 og y = 2 så Z = -2. Merk at verdien z = g (x, y) Det er uavhengig av verdien som er tilordnet variabelen og.

På den annen side, hvis overflaten krysser f (x, y) Med flyet y = c, med c konstant, du har en kurve i flyet ZX: z = -x² - c² + 6.

I dette tilfellet avledet av z med respekt for x sammenfaller med det delvise derivatet av f (x, y) med respekt for x: d_x Z = ∂_xF .

Når du evaluerer i paret (x = 1, y = 2) Det delvise derivatet på det tidspunktet ∂_xF (1.2) Det tolkes som skråningen på linjens tangent til kurven z = -x² + 2 på punktet (x = 1, y = 2) Og verdien av denne skråningen er -2.

Referanser

1. Ayres, f. 2000. Beregning. 5ed. Mc Graw Hill.
2. Delvis derivater av en funksjon i flere variabler. Gjenopprettet fra: Building.UPM.er.
3. Leithold, l. 1992. Beregning med analytisk geometri. Harla, s.TIL.
4. Purcell, e. J., Varberg, d., & Rigdon, s. OG. (2007). Beregning. Mexico: Pearson Education.
5. Gorostizaga J. C. Delvis derivater. Gjenopprettet fra: ehu.Eus
6. Wikipedia. Delvis derivat. Gjenopprettet fra: er.Wikipedia.com.