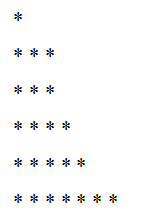Tilsetningsstoffdekomponering

De Tilsetningsstoffdekomponering av et positivt heltall er å uttrykke det som en sum av to eller flere positive tall. Dermed har vi at nummer 5 kan uttrykke det som 5 = 1+4, 5 = 2+3 eller 5 = 1+2+2. Hver av disse måtene å skrive nummer 5 er det vi vil kalle additiv nedbrytning.

Hvis vi tar hensyn, kan vi se at uttrykk 5 = 2+3 og 5 = 3+2 representerer den samme sammensetningen; Begge har de samme tallene. Men bare for et spørsmål om komfort blir vanligvis skrevet hver av annonsene etter kriteriene fra minst til største.

Tilsetningsstoffdekomponering

Som et annet eksempel kan vi ta nummer 27, som vi kan uttrykke det som:

27 = 7+10+10

27 = 9+9+9

27 = 3+6+9+9

27 = 9+18

Additiv nedbrytning er et veldig nyttig verktøy som lar oss styrke vår kunnskap om nummereringssystemer.

Kanonisk additiv nedbrytning

Når vi har tall på mer enn to figurer, er en bestemt form for nedbrytning av dem i multiplene 10, 100, 1000, 10.000 osv., som utgjør det. Denne måten å skrive et hvilket som helst tall kalles kanonisk additiv dekomponering. For eksempel kan nummer 1456 dekomponere det som følger:

1456 = 1000 + 400+ 50 + 6

Hvis vi har nummer 20 846 295, vil din kanoniske additiv nedbrytning være:

20 846 295 = 20 000 000 + 800 000 + 40 000 + 6000 + 200 + 90 +5.

Takket være denne nedbrytningen kan vi se at verdien av et gitt siffer er gitt av den posisjonen det opptar. La oss ta som et eksempel tallene 24 og 42:

24 = 20 + 4

42 = 40 +2

Her kan vi se at i 24 har de 2 en verdi på 20 enheter og på 4 en verdi på 4 enheter; På den annen side, i 42 har de 4 en verdi av 40 enheter og de to av to enhetene. Selv om begge tallene bruker de samme sifrene, er verdiene deres helt forskjellige etter posisjonen de opptar.

Kan tjene deg: x kvadrat

applikasjoner

En av applikasjonene som vi kan gi til additiv nedbrytning er i visse typer demonstrasjoner, der det er veldig nyttig å se et positivt heltall som andres sum.

Eksempelsteorem

La oss som et eksempel følgende teorem med sine respektive demonstrasjoner.

- Være z et helt antall 4 sifre, da er z deles med 5 hvis figuren som tilsvarer enhetene er null eller fem.

Demonstrasjon

La oss huske hva som er delbarhet. Hvis vi har "A" og "B" hele tall, sier vi at "A" deler "B" hvis det er et heltall "C" slik at B = A*C.

En av egenskapene til delbarhet forteller oss at hvis "A" og "B" er delbar mellom "C", så er også subtraksjonen "A-B" også.

Være z et helt antall 4 sifre; Derfor kan vi skrive til z og z = abcd.

Ved å bruke kanonisk additiv dekomponering må vi:

Z = a*1000 + b*100 + c*10 + d

Det er tydelig at en*1000 + b*100 + c*10 er delbar mellom 5. Dette er grunnen til at vi har at Z er delbar mellom 5 hvis Z - (A*1000 + B*100 + C*10) er delbar mellom 5.

Men z - (A*1000 + B*100 + C*10) = D og D er et enkelt figurnummer, så den eneste måten å være delbar mellom 5 er at det er 0 eller 5.

Derfor er z delbar mellom 5 hvis d = 0 eller d = 5.

Merk at hvis Z har n sifre, er demonstrasjonen nøyaktig den samme, endrer det bare at vi nå ville skrevet z = a₁TIL₂… TIL_n Og målet ville være å bevise det_n er null eller fem.

Partisjoner

Vi sier at en partisjon av et positivt heltall er en måte vi kan skrive et tall som en sum av positive heltall.

Kan tjene deg: konvergensradio: Definisjon, eksempler og øvelser løst

Forskjellen mellom en additiv nedbrytning og en partisjon er at selv om det i den første blir søkt at den i det minste kan deles inn i to eller flere, i partisjonen denne begrensningen.

Dermed har vi følgende:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+2+2

Ovennevnte er partisjoner på 5.

Det vil si at vi har at all additiv nedbrytning er en partisjon, men ikke all partisjon er nødvendigvis en additiv nedbrytning.

I tallteori garanterer den grunnleggende teoremet for aritmetiske garantier at hvert helt tall kan skrives unikt som et produkt av søskenbarn.

Når partisjonene studeres, er målet å bestemme hvor mange måter et positivt heltall kan skrives som summen av andre heltall. Derfor definerer vi partisjonsfunksjonen som presentert nedenfor.

Definisjon

Partisjon P (n) -funksjon er definert som antall måter et positivt heltall n kan skrives som en sum av positive heltall.

Tilbake til eksemplet på 5, må vi:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+1+3

5 = 1+2+2

5 = 1+1+1+2

5 = 1+1+1+1+1

På denne måten p (5) = 7.

Grafer

Både partisjoner og additive nedbrytninger av et tall n kan representeres geometrisk.  Anta at vi har en additiv nedbrytning av n. I denne nedbrytningen kan tilleggene fikses slik at medlemmene i summen bestilles fra minst til største. Så det er verdt:

n = a₁ + til₂ + til₃ +… + A_r med

til₁ ≤ a₂ ≤ a₃ ≤ ... ≤ a_r.

Vi kan graf sa nedbrytning som følger: i en første rad markerer vi a₁-poeng, så i det følgende markerer vi₂-poeng, og så videre til de når_r.

Kan tjene deg: ulikhet i trekanten: demonstrasjon, eksempler, løste øvelser

La oss ta som et eksempel nummer 23 og dets neste nedbrytning:

23 = 5 + 4 + 7 + 3 + 1 +3

Vi bestiller denne nedbrytningen, og vi har:

23 = 1 + 3 + 3 + 4+ 5 + 7

Den tilsvarende grafen ville være:

På samme måte, hvis vi leser denne grafen vertikalt i stedet horisontalt, kan vi få en nedbrytning som muligens er forskjellig fra forrige. I eksemplet med de 23 skiller følgende:

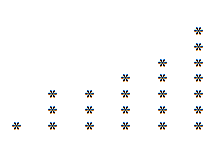
Så vi har at 23 Vi kan også skrive det som:

23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.