Vinkelforskyvning

Hva er vinkelforskyvning?

Han Vinkelforskyvning Det er endringen eller variasjonen i vinkelposisjonen at et objekt i rotasjonsopplevelser, vanligvis målt i radianer eller andre tiltak gitt for svinger, for eksempel karakterer eller revolusjoner.

Når et objekt dreier seg om en fast akse, bestemmes dens vinkelforskyvning ved å måle vinkelen feid av en linje som passerer gjennom et hvilket som helst punkt i kroppen som krysser rotasjonsaksen, det vil si en radial linje.

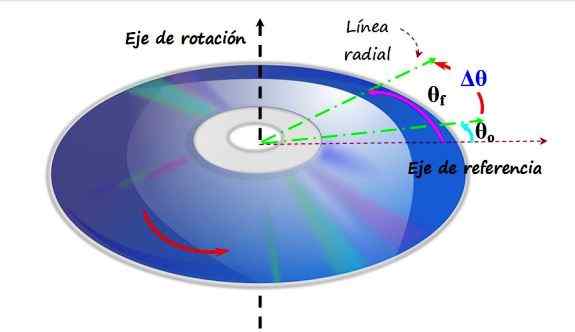En kompakt plate eller CD dreier seg i en antihoranant retning rundt en vertikal rotasjonsaks. Når du går fra vinkel θo til θf, sies det at det har opplevd en vinkelforskyvning. Kilde: f. Zapata.

I den øvre figuren er det en CD som roterer i en anti -Horary retning, og er dens rotasjonsakse den vertikale aksen. En referanseakse er plassert på planet til CDen, som tilsvarer vinkelen 0 radianer eller 0. Den grønne linjen er en radiell linje, som opprinnelig danner en vinkel θ_enten Med referansen. Dette er din opprinnelige stilling.

Senere flytter den grønne linjen til en ny stilling som heter θ_F, Og opplevelsen som oppleves, kalt Δθ er ganske enkelt:

Δθ = θ_F - θ_enten

Ethvert punkt P for CDen opplever den samme vinkelforskyvningen i en viss tidsintervall, bortsett fra sentrum, som er her rotasjonsaksen passerer og forblir i ro.

Formler og ligninger

Det er et objekt som dreier seg om en fast akse eller som overlater skjermen til leseren. Og innenfor det er det punkt P, lokalisert i en avstand R av rotasjonsaksen og beskriver radio R -omkretser.

Dette sees i den følgende figuren, som viser et skjæreobjekt, sett i strid med klokken nåler. Det aktuelle punktet er i vinkelposisjonen θ, målt fra referanseaksen, som i dette tilfellet er den horisontale aksen.

Kan tjene deg: Additive Principle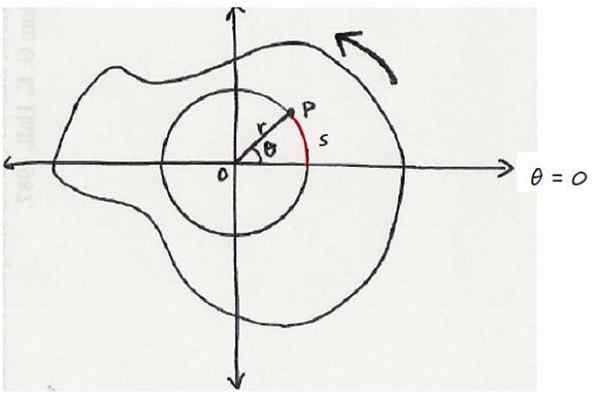Et objekt som roterer i en anti -Horary forstand. Rotasjonsaksen kommer ut vinkelrett på skjermen. Kilde: Wikimedia Commons.

Ved konvensjon, til rotasjonen i antihorarial forstand, er det tildelt positiv forstand, mens rotasjonen i en plan har et negativt tegn.

Når punktet P sverger vinkelen θ, reiser den samtidig buen. Ettersom θ er en sentral vinkel, siden dens toppunkt okkuperer sentrum av omkretsen, blir det oppfylt at:

Med θ uttrykt i radianer.

Vinkelforskyvningen er:

Δθ = θ_endelig  - θ_første

For eksempel, hvis P startet med θ_første = 0 rad og er deretter i θ_endelig = 0.8 rad, dens vinkelforskyvning er fra:

Δθ = 0.8 rad - 0 rad =  0.8 rad

Andre punkter i objektet kan innta forskjellige vinkelposisjoner, men alle opplever den samme vinkelforskyvningen. Imidlertid reiser de mest avsidesliggende partiklene fra midten større avstander, siden s = r⋅θ.

Vinkler måler

I rotasjonen er det vanlig å finne vinklene målt i radianer, men de finnes også i grader og revolusjoner eller svinger. I problemløsning er det nødvendig å flytte fra disse enhetene til radianer.

1 Revolusjon tilsvarer en fullstendig sving, det vil si når en fullstendig vending ødelagt, har den blitt 360 º og disse tilsvarer 2π radianer, siden i så fall turnerte poenget en bue lik 2πr:

Men forenkling kan den tidligere ekvivalensen uttrykkes som følger:

π Radianer = 180º

Hvordan beregnes vinkelforskyvning?

Vinkelforskyvningen kan beregnes analogt med hvordan forskyvningen i bevegelsen beregnes i en dimensjon, etter en viss bevegelsesmodell. For dette er den gjennomsnittlige vinkelhastigheten definert som vinkelforskyvningen Δθ i et gitt tidsintervall ΔT:

Der gjennomsnittlig vinkelhastighet er betegnet som ω_m og er gitt i radianer/s i enheter av det internasjonale systemet hvis.

Kan tjene deg: Hvordan få vinkelen på en trekant? (Eksempel)

Øyeblikkelig vinkelhastighet er grensen for gjennomsnittlig vinkelhastighet når ΔT → 0:

Det vil si at det er den første avledet fra vinkelposisjonen med hensyn til tid. På sin side kan en vinkelakselerasjon defineres, betegnes som α, noe som tilsvarer derivatet eller endringshastigheten for vinkelhastighet med hensyn til tid:

Som også kan tolkes som den andre avledet fra vinkelposisjonen med hensyn til tid.

Det viktige er at to bevegelsesmodeller kan etableres i analogi med de rettlinjede bevegelsene, siden selv om rotasjonene er utført i planet, er en enkelt vinkelkoordinat tilstrekkelig til å etablere posisjonen til et hvilket som helst punkt for objektet.

Ensartet sirkulær bevegelse

I den ensartede sirkulære bevegelsen er vinkelhastigheten konstant, det vil si at den gjennomsnittlige vinkelhastigheten er lik øyeblikkelig vinkelhastighet. Ettersom vinkelakselerasjon α er lik 0, kan du skrive følgende ligning for posisjonen som en funksjon av tid:

θ = θ_enten + ωt

Hvor θ_enten Det er den første posisjonen til mobilen.

Jevn akselerert sirkulær bevegelse

I dette tilfellet er vinkelakselerasjon α konstant, og i analogi med den jevnt varierte rettlinjede bevegelsen kan følgende ligninger skrives:

• θ = θ_enten + Ω_enten T + ½ αT²
• Ω = ω_enten + αt 
• Ω² = Ω_enten² + 2α ∙ Δθ

Trening løst

Første trening

Det kan antas at jorden er et stivt objekt som dreier seg om en fast akse og at dens rotasjon er nesten ensartet. I tidsintervallet Δt = 12 H finn:

a) Vinkelforskyvningen av jorden

b) Din vinkelhastighet

c) Vinkelakselerasjon i løpet av det tidsintervallet.

Løsning på

Når du vet at om 24 timer tar jorden en fullstendig sving rundt aksen, om 12 timer vil du ha snudd halvparten av fanget, det vil si π Radianes. Hvis det anses som en del av θ_første = 0 rad, da er vinkelforskyvningen:

Kan tjene deg: Multiplikativ prinsipp: telleteknikker og eksempler

Δθ = π radianer

Løsning b

Ettersom rotasjonen er ensartet, er vinkelhastigheten mellom vinkelforskyvning og tid, i tillegg 1 time = 3600 s:

Ω = π rad / 12 h = π rad / (12 x 3600) s = 0.000073 rad/s.

Løsning c

Vinkelakselerasjon er ugyldig, siden jordens rotasjon er ensartet.

Andre trening

Juan har kjørt en avstand på 35 meter på et sirkulært friidrettsbane hvis radius er lik 7 meter. Beregn vinkelforskyvningen som Juan har gjort.

Løsning

Siden avstanden til den reiste buen og omkretsens radius er kjent, kan den andre formelen brukes for å kjenne vinkelforskyvningen laget av Juan. Ved å bruke formelen beskrevet ovenfor må du θ = 35/7 = 5 radianer.

Tredje øvelse

Hvis Mario må i kjøretøyet sitt, halvparten av et sirkulært racerbane, hva er vinkelforskyvningen som Mario har gjort?

Løsning

I denne øvelsen vil den første formelen gjelde. Siden det er kjent at Mario har reist halvparten av banen, kan det antas at han startet løpet ved vinkel 0 °, og da han nådde halvparten av omkretsen har han reist 180 °. Derfor er svaret 180 ° -0 ° = 180 ° = π radianer.

Fjerde øvelse

Maria har et sirkulært basseng. Hunden din løper rundt bassenget og kjører en avstand på 18 meter. Hvis bassengradiusen er 3 meter, hva er vinkelforskyvningen laget av Marias kjæledyr?

Løsning

Siden bassenget er sirkulært og radiusen til det er kjent, kan du fortsette å bruke den andre formelen.

Det er kjent at radius er lik 3 meter, og avstanden som er reist av kjæledyret er lik 18 meter. Derfor er vinkelforskyvningen utført lik θ = 18/3 = 6 radianer.

Referanser

1. Katz, d. 2013. Fysikk for forskere og ingeniører. Grunnlag og tilkoblinger. Cengage Learning.
2. Rex, a. 2011. Fundamentals of Physics. Pearson.
3. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1. Pearson.
4. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning.
5. Tipler, s. (2006). Fysikk for vitenskap og teknologi. 5. utg. Volum 1. Redaksjon tilbake.