Matte

Forskjell av formler, ligninger, eksempler, øvelser

Forskjell av formler, ligninger, eksempler, øvelser

De Forskjell på terninger Det er et binomial algebraisk uttrykk for formen til3 - b3, Hvor vilkår A og B kan være reelle tall eller algebraiske uttrykk for forskjellige typer. Et eksempel på kuberforskjell er: 8 - x3, Siden 8 kan skrives som 23.

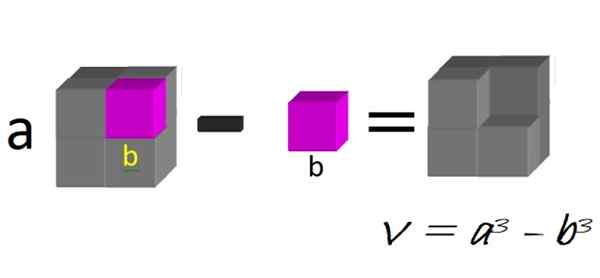
Geometrisk kan vi tenke på en stor kube, fra side A, som den lille munnen på side B trekkes fra, som illustrert i figur 1:

Figur 1. En forskjell på terninger. Kilde: f. Zapata.

Volumet av det resulterende figur er nettopp en forskjell i terninger:

V = a3 - b3

For å finne et alternativt uttrykk observeres det at denne figuren kan deles inn i tre prismer, som vist nedenfor:

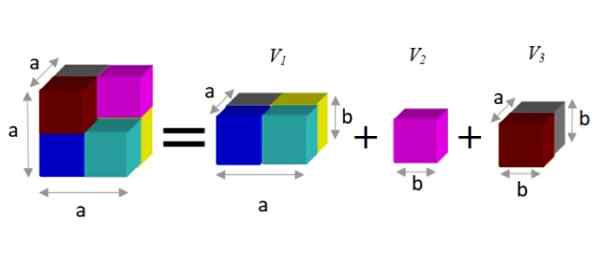Figur 2. Forskjellen i terninger (venstre for likestilling) er lik summen av delvis volum (høyre). Kilde: f. Zapata.

Et prisme har et volum gitt av produktet av sine tre dimensjoner: bredde x høy x dybde. På denne måten er det resulterende volumet:

V = a3 - b3 = a2.b + b3 + til.b2

Faktoren b Det er vanlig for høyre. I tillegg, i figuren vist ovenfor, er det spesielt oppfylt at:

b = (a/2) ⇒ a = b + b

Derfor kan det sies at: b = a - b. Dermed:

til3 - b3 = B (a2 + b2 +til.b) = (a-b) (a2 + til.b + b2)

Denne måten å uttrykke forskjellen i terninger på vil vise seg å være veldig nyttig i mange applikasjoner og ville blitt oppnådd på samme måte, selv om den manglende kubesiden i hjørnet var forskjellig fra B = A/2.

Merk at den andre parentesenDet ser mye ut til det bemerkelsesverdige produktet av summen av summen, men det kryssede uttrykket multipliseres ikke med 2. Leseren kan utvikle høyre side for å bekrefte at den er effektivt oppnådd til3 - b3.

[TOC]

Kan tjene deg: firkantet binomial

Eksempler

Det er flere terninger forskjeller:

1 - m6

til6b3 - 8z12og6

(1/125).x6 - 27.og9

La oss analysere hver og en av dem. I det første eksemplet kan 1 skrives som 1 = 13 og begrepet m6 Det gjenstår: (m2)3. Begge begrepene er perfekte kuber, derfor er forskjellen deres:

1 -m6 = 13 - (m2)3

I det andre eksemplet blir begrepene skrevet om:

til6b3 = (a2b)3

8z12og6 = 23 (z4)3 (og2)3 = (2z4og2)3

Forskjellen på disse terningene er: (a2b)3 - (2z4og2)3.

Endelig er brøkdelen (1/125) (1/53), x6 = (x2)3, 27 = 33 og og9 = (og3)3. Erstatt alt dette i det opprinnelige uttrykket, oppnås det:

(1/125).x6  - 27y9 = [(1/5) (x2)]3 - (3 år3)3

Faktorisering av en terningforskjell

Faktisk forskjellen i kuber forenkler mange algebraiske operasjoner. For å gjøre dette er det nok å bruke formelen som er trukket tidligere:

Figur 3. Faktorisering av forskjellen i terninger og uttrykk for en bemerkelsesverdig kvotient. Kilde: f. Zapata.

Nå består prosedyren for å anvende denne formelen av tre trinn:

- For det første oppnås den kubiske roten til hvert av vilkårene for forskjellen.

- Da er binomial og trinomial som vises på høyre side av formelen bygget.

- Til slutt erstattes binomial og trinomial for å oppnå den endelige faktoriseringen.

Vi vil illustrere bruken av disse trinnene med hvert av eksemplene på forskjell på terninger foreslått ovenfor og dermed oppnå dets faktoriserte ekvivalent.

Eksempel 1

Faktisk uttrykk 1 -m6   Etter de beskrevne trinnene. Vi begynner med å omskrive uttrykket som 1 -m6 = 13 - (m2)3 For å trekke ut de respektive kubiske røttene til hvert begrep:

Da er binomial og trinomial bygget:

Det kan tjene deg: køteori: historie, modell, hva er det for og eksempler for

A = 1

b = m2

Så:

A - B = 1 - M2

 (til2 +til.b + b2) = 12 + 1.m2 + (m2)2 = 1 + m2 + m4

 Endelig erstattes den i formel A3 - b3 = (a-b) (a2 +til.b + b2):

1 -m6 = (1 - m2) (1 + m2 + m4)

Eksempel 2

Faktorisere:

til6b3 -8z12og6 = (a2b)3 - (2z4og2)3

Siden dette er perfekte kuber, er kubiske røtter øyeblikkelig: a2B og 2Z4og2, Derfra følger det det:

- Binomial: a2B - 2Z4og2

- Trinomial: (a2b)2 + til2b. 2Z4og2 + (til2B +2Z4og2)2

 Og nå er den ønskede faktoriseringen bygget:

til6b3 -8z12og6 = (a2B - 2Z4og2). [(til2b)2 + til2b. 2Z4og2 + (til2B + 2Z4og2)2] =

= (a2B - 2Z4og2). [til4b2 + 22b.z4og2 + (til2B + 2Z4og2)2]

I prinsippet er faktoriseringen klar, men det er ofte nødvendig å forenkle hvert begrep. Da utvikles det bemerkelsesverdige produktet fra en sum - som vises på slutten og deretter legge til lignende vilkår. Husker at kvadratet med en sum er:

(x + y)2 = x2 + 2xy + og2

Den bemerkelsesverdige høyre til høyre utvikler seg på denne måten:

(til2B + 2Z4og2)2 = a4b2 + 4. plass2b.z4og2 + 4Z8og4

 Erstatte utviklingen oppnådd ved faktorisering av forskjellen i terninger:

til6b3 -8z12og6 = (a2B - 2Z4og2). [til4b2 + 22b.z4og2 + til4b2 + 4. plass2b.z4og2 + 4Z8og4] =

Til slutt, gruppering av lignende vilkår og fabrikker de numeriske koeffisientene, som alle er par, oppnås det:

(til2B - 2Z4og2). [24b2 + 62b.z4og2 + 4Z8og4] = 2 (a2B - 2Z4og2). [til4b2 + 32b.z4og2 + 2Z8og4]

Eksempel 3

Factorize (1/125).x6  - 27y9 Det er mye enklere enn forrige sak. Først identifiseres ekvivalenter av A og B:

A = (1/5) x2

B = 3y3

Så erstattes de direkte på formelen:

(1/125).x6  - 27y9 = [(1/5) x2 - 3y3]. [(1/25) x4 + (3/5) x2og3 + 9y6]

Trening løst

Forskjellen i terninger har som vi har sagt en rekke applikasjoner i algebra. La oss se på noen:

Kan tjene deg: 5 kjennetegn på det kartesiske flyet

Oppgave 1

Løs følgende ligninger:

a) x5 - 125 x2 = 0

b) 64 - 729 x3 = 0

Løsning på

Først er ligningen faktor på denne måten:

x2 (x3 - 125) = 0

Ettersom 125 er en perfekt kube, er parentesis skrevet som en forskjell i kuber:

x2 . (x3 - 53) = 0

Den første løsningen er x = 0, men vi finner mer hvis vi lager x3 - 53 = 0, da:

x3 = 53 → x = 5

Løsning b

Venstre side av ligningen skrives om som 64 - 729 x3 = 43 - (9x)3. Derfor:

43 - (9x)3 = 0

Siden eksponenten er den samme:

9x = 4 → x = 9/4

Oppgave 2

Faktorisere uttrykk:

(x + y)3 - (X - y)3

Løsning

Dette uttrykket er en forskjell i terninger, hvis vi i faktoriseringsformelen legger merke til at:

A = x+ og

b = x- y

Så bygges binomialen først:

a - b = x+ y - (x- y) = 2y

Og nå trinomial:

til2 + til.b + b2 = (x+ y)2 + (x + y) (x-y) + (x-y)2

Bemerkelsesverdige produkter er utviklet:

(x+ y)2 = x2 + 2xy +og2

(x+y) (x-y) = x2- og2

(x- y)2 = x2 - 2xy +og2

Da må du erstatte og redusere lignende vilkår:

til2 + til.b + b2 = x2 + 2xy +og2+ x2- og2+ x2 - 2xy +og2 = 3x2 + og2

Faktorisering resulterer i:

(x + y)3 - (X - y)3 = 2y. (3x2 + og2)

Referanser

  1. Baldor, a. 1974. Algebra. Venezuelansk kulturell redaksjon S.TIL.
  2. CK-12 Foundation. Sum og forskjell på terninger. Gjenopprettet fra: CK12.org.
  3. Khan Academy. Kubes forskjellsfaktorisering. Gjenopprettet fra: er.Khanacademy.org.
  4. Matematikk er morsom avansert. Forskjell på to terninger. Gjenopprettet fra: matematikk.com
  5. Unam. Faktorisering av en terningforskjell. Hentet fra: DCB.Fi-C.Unam.MX.