Forskjell mellom sirkel og omkrets (med eksempler)

De Forskjell mellom sirkel og omkrets Det er følgende: Sirkelen er en flat, konturert eller avgrenset overflate ved en sirkel, mens sistnevnte er en flat kurve.

Ofte er begge konseptene forvirrede, siden de er relatert, men du må alltid huske at omkretsen er kanten av sirkelen, mens den inneholder omkretsen og alle punktene interiør til den.

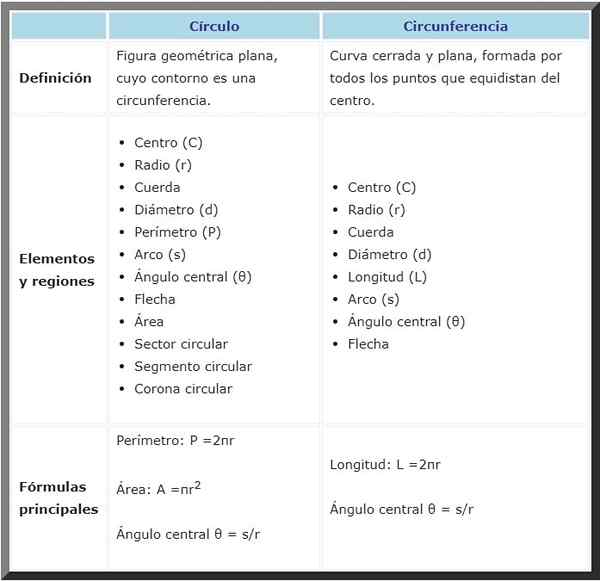
Begge har mange elementer til felles, for eksempel sentrum, radius og diameter, blant andre, i henhold til følgende sammenlignende tabell:

	Sirkel	Omkrets
Definisjon	Flat geometrisk figur, hvis kontur er en omkrets.	Lukket og flat kurve, dannet av alle punktene som er ekvist i sentrum.
Elementer og regioner	Sentrum (c) Radio (r) Tau Diameter (D) Omkrets (P) Bue (er) Sentral vinkel (Θ) Pil Område Sirkulær sektor Sirkulært segment Sirkulær krone	Sentrum (c) Radio (r) Tau Diameter (D) Lengde (l) Bue (er) Sentral lengde (Θ) Pil
Formler	Omkrets: P = 2π⋅r Område: A =πR2 Sentral vinkel: Θ= S/R	Lengde: L = 2π⋅r Sentral vinkel: Θ= S/R

[TOC]

Sirkel: Definisjon, egenskaper og deler

En sirkel er en flat geometrisk figur, som inkluderer alle punktene i omkretsen som danner konturen og også alle interiørpunktene.

Av denne grunn er det preget av å ha:

-Kant eller omkrets, som er sirkelomkrets.

-Et overfladisk område.

Elementene i sirkelen

Hver sirkel har følgende deler eller elementer:

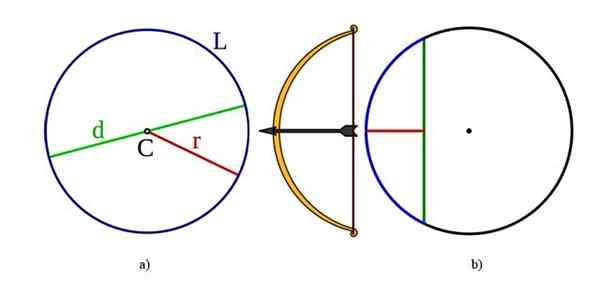Elementer av sirkelen, også felles for omkretsen: til venstre i a) er sentrum d, diameter d, radius r og lengde l l. Rett på b) Det er tau og sagita eller pil. Kilde: Wikimedia Commons.

Senter: Hva er punkt C, som tilsvarer alle punktene i kanten.

Kan tjene deg: Arc (geometri): mål, buertyper, eksempler

Tau: segment som blir med to punkter på kanten av sirkelen. I figur B) til høyre er det det mørkere grønne segmentet.

Diameter: lettere grønt segment, betegnet "d" i figur A), som blir med to punkter i kanten og samtidig går gjennom sentrum. Diameteren er også et tau, den lengste av alle, så det er kjent som Major tau.

Radio: betegnet med “R” i figur A), er det det røde segmentet som blir med i sentrum av sirkelen med et punkt på kanten. Målet er halvparten av diameteren.

Bue: en del av konturen som er mellom to punkter av dette, i blått i figur B).

Sentral vinkel: Det er vinkelen hvis toppunkt er i sentrum eller og sidene er radioer i sirkelen.

Pil: segment vinkelrett på et tau (i rødt i figur B), som blir med i sentrum av tauet med et poeng av kanten.

Lengde eller omkrets: Det er målet på sirkelkonturen, betegnet l. Det avhenger av radio R og er proporsjonal med det irrasjonelle tallet π:

π = 3.1416 ..

Så det:

L = 2π⋅r

Sirkulære regioner

Å være en flat figur, sirkelen har et totalt areal og også forskjellige regioner. Det mest kjente er følgende:

Sirkelområde: Det er proporsjonalt med kvadratet av radius, proporsjonalitetskonstanten er tallet π.

Ringer sirkelområdet, er det uttrykt som:

A = πr²

Sirkulært segment: Det er en del av sirkelen begrenset av den blå buen og det mørkegrønne tauet i figur B.

Kan tjene deg: Tilleggsvinkler: Hva er, beregning, eksempler, øvelser

Sirkulær sektor: Det er også et område av sirkelen, men inneholdt mellom to radioer og den tilsvarende buen.

Sirkulær krone: Den er formet som en ring og er begrenset av to konsentriske omkretser, utenfor radio Menor og inne i radiorordføreren.

Omkrets: dEfinisjon, egenskaper og deler 

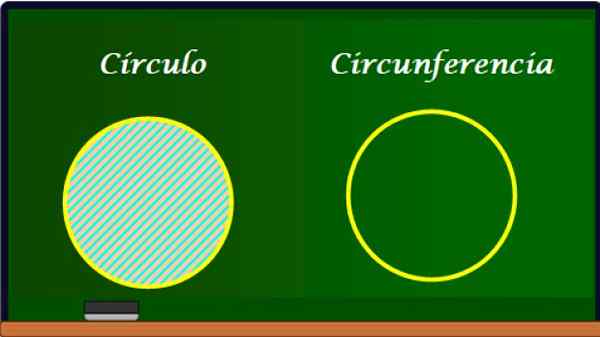En sirkel og dens omkrets. Kilde: f. Zapata.

Omkretsen er kanten av sirkelen og har derfor mange elementer til felles med dette. Omkretsen har imidlertid ikke noe område, for siden den er en kurve har den bare lengde l.

Omkretsen er formelt definert som settet med alle punktene som tilsvarer et annet punkt kjent som sentrum.

Interiørpunktene er ikke inkludert, siden disse tilsvarer sirkelen.

Elementene i omkretsen

Mange av elementene i omkretsen er de samme som sirkelen, unntatt de som refererer til områder og regioner, så den øvre figuren fungerer som en referanse.

Vi har da:

Senter: betegnet med C og noen ganger også som O, holder alle punktene i omkretsen samme avstand med den.

Tau: segment som blir med to punkter som tilhører omkretsen.

Diameter: Den blir også med på to punkter i omkretsen, men passerer alltid gjennom sentrum av det samme.

Radio: Det er avstanden mellom sentrum og et hvilket som helst punkt i omkretsen.

Bue: Det er en del av omkretsen.

Sentral vinkel: Det er vinkelen med toppunktet i sentrum C og to like sider som måler akkurat som radioen.

Pil: segment vinkelrett på et tau, som blir med i sentrum av dette med det tilsvarende punktet i omkretsen.

Kan tjene deg: Multiplikativ prinsipp: telleteknikker og eksempler

Lengde eller omkrets: Det er målet på omkretsen, som vi har sett, er proporsjonalt med tallet π = 3.1416 ... og den beregnes med formelen:

L = 2π⋅r

Omkretsligningen

Et punkt P tilhører en omkrets så lenge avstanden til et annet punkt C er lik r, radioen.

Ethvert punkt på det kartesiske flyet har koordinater (X, y) og avstandens kvadrat d Mellom to av dem, P₁(x₁,og₁) Og s₂(x₂,og₂), er gitt av formelen:

d₂² = (x₂ - x₁)² +  (og₂ - og₁)²

La oss ta poenget med koordinater (x, y) og til koordinatpunkt C (H, K). Erstatning, den forrige ligningen ville være slik:

(X - h)² +  (Y- k)² = r²

Dette er omkretsligningen, som ethvert punkt på den tilfredsstiller. Hvis sentrum av omkretsen sammenfaller med opprinnelsen til koordinatsystemet, er H = k = 0 og ligningen forenklet:

x² + og² = r²

La oss se på et eksempel på hvordan du bruker ligningen og svarer på dette problemet: hører poenget (4.6) til omkretsen (x - 1)² +  (og - 2)² = 25?

For å finne ut at koordinatene til punktet i ligningen erstattes, og hvis det er en likhet, hører poenget til omkretsen:

(4 - 1)² +  (6 - 2)² = 3² + 4² = 9 + 16 = 25

Og som 25 = 25, konkluderes det med at (4.6) tilhører omkretsen.

Referanser

1. Gratis matematikkopplæringer. Område og omkrets av en sirkel - Geometri -kalkulator. Gjenopprettet fra: Analysemath.com.
2. Matematikk åpen referanse. Omkrets, omkrets av en sirkel. Gjenopprettet fra: Mathpenref.com.
3. Scienting. Hvordan finne omkretsen til en sirkel. Gjenopprettet fra: Scienting.com.
4. Stewart, J. 2006. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
5. Zill, d. 1984. Algebra og trigonometri. McGraw Hill.