Forskjeller mellom hastighet og hastighet (med eksempler)

De forskjeller mellom hastighet og hastighet Det er, selv om begge er relaterte fysiske mengder. På vanlig språk brukes det ene begrepet om hverandre som om de var synonyme, men i fysikk er det nødvendig å skille dem.

I denne artikkelen er begge begrepene definert, er forskjellene indikert og forklart, med eksempler, hvordan og når det ene eller det andre gjelder. For å forenkle vi vurderer en bevegelig partikkel og derfra vil vi gjennomgå begrepene hastighet og hastighet. 

	Hastighet	Hastighet
Definisjon	Det er den tilbakelagte avstanden per tidsenhet.	Er forskyvningen (eller endring av posisjon) i hver tidsenhet.
Notasjon	v	v
Type matematisk objekt	Klatre.	Vektor.
Formel (for en begrenset tidsperiode)*	v = ΔS/Δt	v = ΔR/Δt
Formel (for et øyeblikk av gitt tid) **	v = ds/dt = s '(t)	v = dr/dt = r '(t)
Forklaring av formelen	*Lengden på stien som er reist delt mellom tidsperioden som ble brukt til å reise den.** I øyeblikkelig hastighet har tidsspennet en tendens til null. ** Den matematiske operasjonen er derivatet av banebuen som en funksjon av tid med hensyn til tiden T.	*Vektorforskyvning delt på tidsperioden der forskyvningen skjedde. ** I øyeblikkelig hastighet har tidsperioden en tendens til null. ** Den matematiske operasjonen er derivatet av stillingen i tide.
Kjennetegn	For å uttrykke det er det bare et positivt reelt tall, uavhengig av de romlige dimensjonene som bevegelsen skjer. ** Øyeblikkelig hastighet er den absolutte verdien av øyeblikkelig hastighet.	Mer enn ett reelt tall (positivt eller negativt) kan være nødvendig for å uttrykke det, avhengig av de romlige dimensjonene som bevegelsen finner sted. ** Den øyeblikkelige hastighetsmodulen er øyeblikkelig.

Eksempler med ensartet hurtighet på rette seksjoner

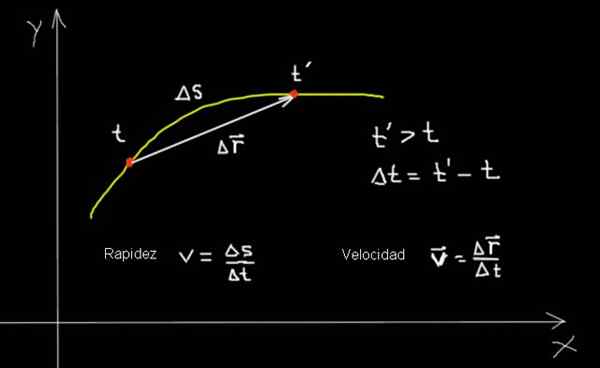
Hastighet og hastighet på en partikkel som beveger seg i en kurve. Utarbeidet av: f. Zapata.

I forrige tabell ble flere aspekter av hastighet og hastighet oppsummert. Og for å utfylle, vurderes flere eksempler som illustrerer konseptene som er involvert og deres forhold:

Kan tjene deg: paramagnetisme

- Eksempel 1

Anta at en rød maur beveger seg etter en rett linje og i retningen som er angitt i følgende figur.

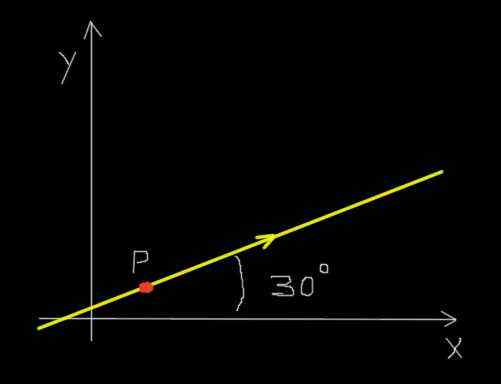En maur på den rettsinale banen. Kilde: f. Zapata.

I tillegg beveger myren seg jevnt slik at den beveger seg en avstand på 30 millimeter i en tidsperiode på 0,25 sekunder. 

Bestem hastigheten og hastigheten på mauren.

Løsning 

Myrets hastighet beregnes ved å dele avstanden ΔS Toure Tour Δt.

V = ΔS/ΔT = (30 mm)/(0,25s) = 120 mm/s = 12 cm/s

Myrets hastighet beregnes ved å dele forskyvningen Δr Mellom den tidsperioden som nevnte fortrengning ble foretatt.

Forskyvningen var 30 mm i retning 30º med hensyn til x -aksen, eller i en kompakt form: 

Δr = (30 mm ¦ 30º)

Det kan bemerkes at forskyvningen består av en størrelse og en adresse, siden den er en vektormengde. Alternativt kan forskyvning uttrykkes i henhold til dens kartesiske komponenter X og Y, på denne måten:

Δr = (30 mm* cos (30º); 30 mm* uten (30º)) = (25,98 mm; 15,00 mm)

Myrets hastighet beregnes ved å dele forskyvningen mellom tidsperioden den ble utført i:

v = Δr/Δt = (25,98 mm / 0,25 s; 15,00 mm / 0,25 s) = (103,92; 60,00) mm / s

Denne hastigheten i kartesiske komponenter x og y y i enheter av cm/s er:

v = (10.392; 6.000) cm/s.

Alternativt kan hastighetsvektoren uttrykkes i dens polare form (modul ¦ retning) som vist:

v = (12 cm/s ¦ 30º).

Merk: I dette eksemplet ettersom hastigheten er konstant, sammenfaller gjennomsnittlig hastighet og øyeblikkelig hastighet. Det er bevist at den øyeblikkelige hastighetsmodulen er øyeblikkelig rask.

Kan tjene deg: tetthet

Eksempel 2

Den samme mauren til det forrige eksemplet går fra A til B, etter B til C og til slutt fra C til A, etter den trekantede banen vist i følgende figur.

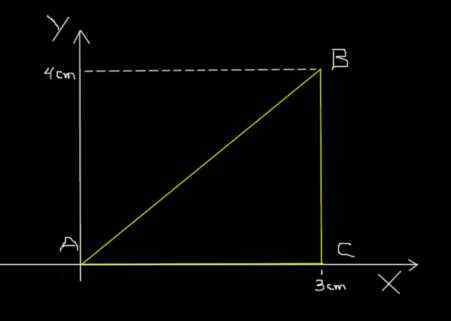Trekantet sti av en maur. Kilde: f. Zapata.

Avsnitt AB reiser på 0,2s; BC reiser på 0,1s og til slutt reiser CA på 0,3s. Beregn gjennomsnittets hastighet på ABCA -ruten og gjennomsnittshastigheten til ABCA -ruten.

Løsning 

For å beregne gjennomsnittshastigheten til mauren, begynner vi med å bestemme den totale tilbakelagte distansen:

ΔS = 5 cm + 4 cm + 3 cm = 12 cm.

Tidsperioden som brukes til hele reisen er:

Δt = 0,2s + 0,1s + 0,3s = 0,6 s.

Så den gjennomsnittlige hastigheten på myren er:

V = ΔS/Δt = (12 cm)/(0,6s) = 20 cm/s.

Deretter beregnes gjennomsnittshastigheten til mauren på ABCA -ruten. I dette tilfellet er forskyvningen gjort av mauren:

ΔR = (0 cm; 0 cm)

Dette er fordi forskyvningen er forskjellen mellom den endelige posisjonen mindre startposisjonen. Ettersom begge posisjonene er de samme, er forskjellen deres ugyldig, noe som resulterer i en nullforskyvning.

Denne nullforskyvningen ble utført i en tidsperiode på 0,6s, så den gjennomsnittlige maurtypen var:

v =(0 cm; 0 cm)/ 0.6s = (0; 0) cm/ s.

Konklusjon: Gjennomsnittshastighet 20 cm/s, Men gjennomsnittshastigheten er null i ABCA -ruten.

Eksempler med jevn hurtighet på buede seksjoner

Eksempel 3

Et insekt beveger seg på en sirkel med 0,2 m radius med ensartet hastighet, slik at det starter fra A og når B, den reiser ¼ omkrets ved 0,25 s.

Kan tjene deg: hydraulisk presse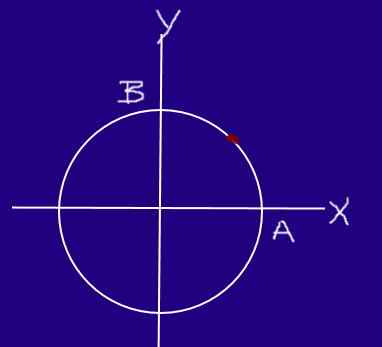Sirkulær seksjonsinsekt. Kilde: f. Zapata.

Bestem hastigheten og hastigheten til insektet i seksjon AB.

Løsning 

Lengden på omkretsbuen mellom A og B er:

ΔS = 2πr /4 = 2π (0,2 m) /4 = 0,32 m.

Bruke definisjonen av gjennomsnittshastighet du har:

V = ΔS/ΔT = 0,32 m/0,25 s = 1,28 m/s.

For å beregne gjennomsnittshastigheten er det nødvendig å beregne forskyvningsvektoren mellom startposisjonen A og den endelige B:

Δr = (0; r)-(r; 0) = (-r; r) = (-0,2; 0,2) m

Bruk av gjennomsnittlig hastighetsdefinisjon oppnås:

v = Δr/ Δt = (-0,2; 0,2) m / 0,25s = (-0.8; 0,8) m/s.

Det forrige uttrykket er gjennomsnittshastigheten mellom A og B uttrykt i kartesisk form. Alternativt kan gjennomsnittshastigheten uttrykkes i polarform, det vil si modul og retning:

| v | = ((-0,8)^2 + 0,8^2)^(½) = 1,13 m/s

Adresse = Arctan (0,8 / (-0,8)) = Arcan (-1) = -45º + 180º = 135º med hensyn til x-aksen.

Til slutt er gjennomsnittlig hastighetsvektor i polarform: v =(1,13 m/s ¦ 135º).

Eksempel 4

Forutsatt at startmomentet til insektet i det forrige eksemplet er 0s fra punkt A, er vektorposisjonen din på et øyeblikk noen T er gitt av:

r(t) = [r cos ((π/2) t); R sen ((π/2) t)].

Bestem hastigheten og øyeblikkelig hastighet for ethvert øyeblikk t.

Løsning 

Den øyeblikkelige hastigheten er derivatet med hensyn til stillingen:

v(t) = Dr/dt = [-r (π/2) uten ((π/2) t); R (π/2) cos ((π/2) t)]]

Øyeblikkelig hastighet er modulen til vektoren øyeblikkelig hastighet:

V (t) = | v(T) | = π r / 2^½

Referanser

1. Alonso m., Finn e. Fysikkvolum I: Mekanikk. 1970. Inter -American Education Fund s.TIL.
2. Hewitt, p. Konseptuell fysisk vitenskap. Femte utgave. Pearson.
3. Young, Hugh. Universitetsfysikk med moderne fysikk. 14. utg. Pearson.
4. Wikipedia. Hastighet. Gjenopprettet fra: er.Wikipedia.com
5. Zita, a. Forskjell mellom hastighet og hastighet. Hentet fra: Differensierer.com