Lineær utvidelse hva er, formel og koeffisienter, eksempel

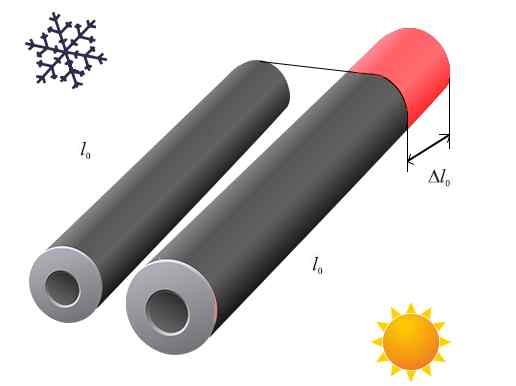
De Lineær utvidelse oppstår når et objekt opplever utvidelse på grunn av en temperaturvariasjon, hovedsakelig i en enkelt dimensjon. Dette skyldes egenskapene til materialet eller dets geometriske form. 

For eksempel i en ledning eller i en bar, når det er en økning i temperaturen er den lange som lider av den største endringen på grunn av termisk utvidelse.

Fugler posert i ledninger. Kilde: Pixabay.

Kablene som fuglene ablaterer i forrige figur lider av en strekning når temperaturen øker; I stedet trekker de inn når de kjøler seg. På samme måte skjer det for eksempel med stolpene som danner skinnene på en jernbane.

[TOC]

Hva er lineær utvidelse?

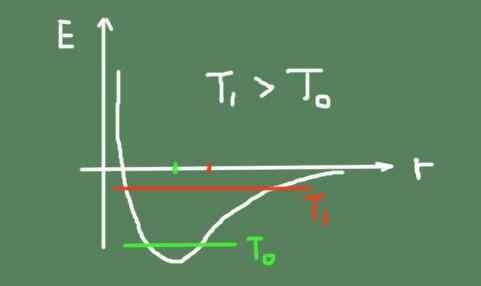
Graf over energien til den kjemiske bindingen kontra den interatomiske avstanden. Kilde: Selvlaget.

I et solid materiale opprettholder atomer sine relative posisjoner mer eller mindre fikset rundt et balansepunkt. På grunn av termisk omrøring svinger de imidlertid alltid rundt det.

Ved å øke temperaturen øker også termisk svingning og fører til at middels svingningsposisjoner endres. Dette er fordi koblingspotensialet ikke akkurat er parabolsk og har asymmetri rundt minimum.

Nedenfor er en figur som skisserer den kjemiske bindingsenergien avhengig av den interatomiske avstanden. Den totale svingningsenergien ved to temperaturer er også vist, og hvordan svingningssenteret beveger seg.

Formel for lineær utvidelse og dens koeffisient

For å måle den lineære utvidelsen, starter vi fra en innledende LE -lengde og en starttemperatur T, fra objektet du vil måle utvidelsen din.

Anta at dette objektet er en stolpe hvis lengde er l og dimensjonene til tverrsnittet er mye lavere enn l.

Kan tjene deg: øyeblikkelig akselerasjon: Hva er det, hvordan det beregnes og øvelser

Først blir dette objektet utsatt for en ΔT temperaturvariasjon, slik at den endelige temperaturen til objektet når varmeeknoren er etablert med varmekilden vil være t '= t+ Δt.

Under denne prosessen vil objektets lengde også ha endret seg til en ny verdi L '= L + ΔL, hvor ΔL er variasjonen i lengden.

Den lineære utvidelseskoeffisienten α er definert som forholdet mellom den relative variasjonen av lengde per enhetens temperaturvariasjon. Følgende formel definerer den lineære utvidelseskoeffisienten α:

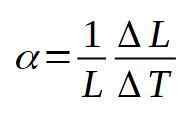I de fleste tilfeller, α Den har en konstant verdi for temperaturer mellom (t - Δt) og (t + Δt).

Dimensjonene til den lineære utvidelseskoeffisienten er temperaturen.

Temperaturen øker lengden på rørets formede faste stoffer. Dette er det som kalles lineær utvidelse. Kilde: Lafer.com

Lineær utvidelseskoeffisient for forskjellige materialer

Neste gang vil vi gi en liste over den lineære utvidelseskoeffisienten for noen typiske materialer og elementer. Koeffisienten beregnes i normalt atmosfæretrykk basert på en omgivelsestemperatur på 25 ° C; og verdien anses som konstant i et område på opptil 100 ° C.

Den lineære utvidelseskoeffisientenheten vil være (° C)^-1.

- Stål: α = 12 ∙ 10^-6 (° C)^-1

- Aluminium: α = 23 ∙ 10^-6 (° C)^-1

- Gull: α = 14 ∙ 10^-6 (° C)^-1

- Kobber: α = 17 ∙ 10^-6 (° C)^-1

- Messing: α = 18 ∙ 10^-6 (° C)^-1

- Jern: α = 12 ∙ 10^-6 (° C)^-1

- Glass: α = (7 til 9) ∙ 10^-6 (° C)^-1

- Kvikksølv: α = 60,4 ∙ 10^-6 (° C)^-1

- Kvarts: α = 0,4 ∙ 10^-6 (° C)^-1

- Diamant: α = 1,2 ∙ 10^-6 (° C)^-1

- Bly: α = 30 ∙ 10^-6 (° C)^-1

Det kan tjene deg: konveksjon varmeoverføring (med eksempler)

- Eik tre: α = 54 ∙ 10^-6 (° C)^-1

- PVC: α = 52 ∙ 10^-6 (° C)^-1

- Karbonfiber: α = -0.8 ∙ 10^-6 (° C)^-1

- Betong: α = (8 til 12) ∙ 10^-6 (° C)^-1

De fleste materialer strekker seg med en temperaturøkning. Noen spesielle materialer som karbonfiber krymper imidlertid med temperaturøkning.

Løst eksempler på lineær ekspansjon

Eksempel 1

En kobberkabel henges mellom to stolper, og lengden på en kjølig dag ved 20 ° C er 12 m. Beregn verdien av lengden på en varm dag ved 35 ° C.

Løsning

Starter fra definisjonen av den lineære utvidelseskoeffisienten, og å vite at for kobber er denne koeffisienten verdt: α = 17 ∙ 10^-6 (° C)^-1

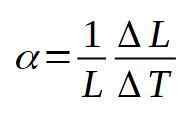
Økningen i lengde er gitt av: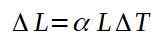

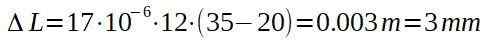
Kobberkabelen gjennomgår en økning i lengden, men dette er bare 3 mm. Det vil si at kabelen går fra å ha 12 000 m til å ha 12,003 m.

Eksempel 2

I en smed, forlater en aluminiumsbar ovnen på 800 grader Celsius, og måler en lengde på 10,00 m. Når den avkjøles til omgivelsestemperaturen på 18 grader Celsius, må du bestemme lengden som baren vil ha.

Løsning

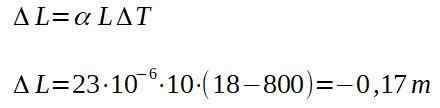
Det vil si at baren, en gang kald, vil ha en total lengde på:

9,83 m.

Eksempel 3

En stålnivet har en diameter på 0.915 cm. Et hull på 0,910 cm er laget på en aluminiumsplate. Dette er de opprinnelige diametrene når omgivelsestemperaturen er 18 ° C.

Ved hvilken minimumstemperatur skal platen varmes opp slik at naglen passerer gjennom hullet? Målet med dette er at når jernet går tilbake til romtemperatur, justeres naglen på platen.

Kan tjene deg: parallellogrammetode: eksempler, løste øvelser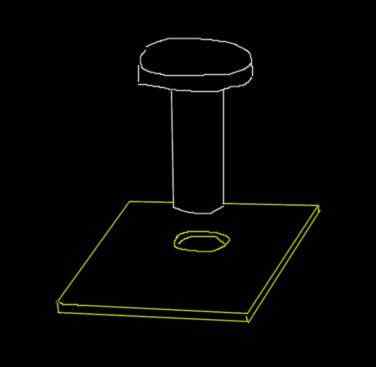Figur for eksempel 3. Kilde: Selvlaget.

Løsning

Selv om platen er et område, er vi interessert i utvidelse av hulldiameteren, som er en endimensjonal mengde.

La oss ringe D₀ til den opprinnelige diameteren på aluminiumsplaten, og D som en gang vil ha oppvarmet.

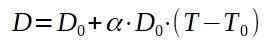
Rydde den endelige temperaturen T, du har:

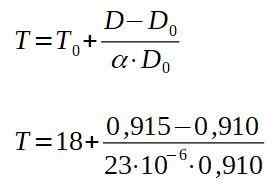
Resultatet av de tidligere operasjonene er 257 ° C, som er den minste temperaturen som platen må varmes opp slik at naglen passerer gjennom hullet.

Eksempel 4

Naglen og plaketten til den forrige øvelsen er plassert sammen i en ovn. Bestem ved hvilken minimumstemperatur ovnen må være slik at stålniven passerer gjennom aluminiumsplatehullet.

Løsning

I dette tilfellet kommer både naglen og hullet til å utsette. Men stålutvidelseskoeffisienten er α = 12 ∙ 10^-6 (° C)^-1, Mens aluminium er α = 23 ∙ 10^-6 (° C)^-1 .

Vi ser da etter en endelig temperatur slik at begge diametrene sammenfaller.

Hvis vi ringer 1 til naglen og 2 til aluminiumsplaten, ser vi etter en endelig temperatur T slik at D₁ = D₂.

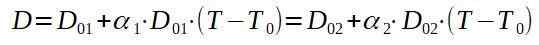
Hvis vi fjerner den endelige temperaturen T, har vi:

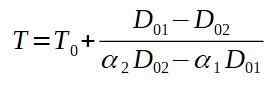
Neste plasserer vi de tilsvarende verdiene.

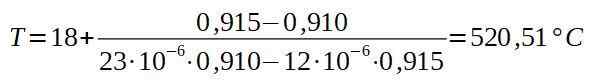
Konklusjonen er at ovnen må være minst 520,5 ° C slik at naglen passerer gjennom aluminiumsplatehullet.

Referanser

1. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. Sjette utgave. Prentice Hall. 238-249.
2. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mac Graw Hill. 422-527.