Poisson distribusjonsformler, ligninger, modell, egenskaper

De Poisson distribusjon Det er en diskret sannsynlighetsfordeling, der du kan vite sannsynligheten for at i en stor prøve og i løpet av et visst intervall, oppstår en hendelse hvis sannsynlighet er liten.

Ofte kan Poissons distribusjon brukes i stedet for binomial distribusjon, så lenge følgende forhold beskrevet er oppfylt: stor prøve og liten sannsynlighet.

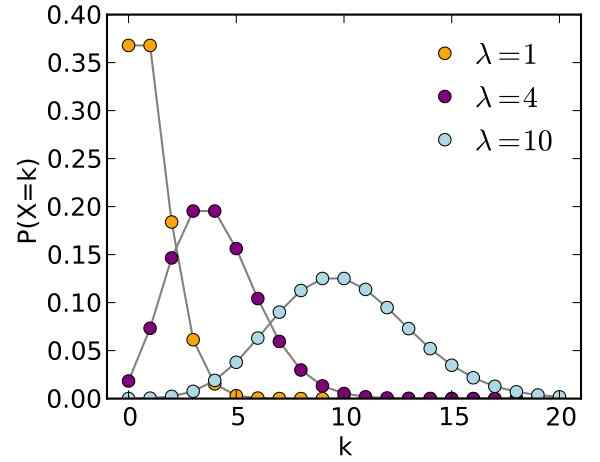
Figur 1. Poisson distribusjonsgraf for forskjellige parametere. Kilde: Wikimedia Commons.

Siméon-Denis Poisson (1781-1840) skapte denne distribusjonen som bærer navnet hans, veldig nyttig når det gjelder uforutsigbare hendelser. Poisson publiserte resultatene i 1837, et forskningsarbeid om sannsynligheten for forekomst av feilaktige strafferettigheter.

Deretter tilpasset andre forskere distribusjonen på andre områder, for eksempel antall stjerner som kan være i et visst volum av rom, eller sannsynligheten for at en soldat ville dø på grunn av en hestes goz.

[TOC]

Formel og ligninger

Den matematiske formen for Poissons distribusjon er som følger:

 - Den tilfeldige variabelen er og

- μ (også noen ganger betegnet som λ) Det er gjennomsnitts- eller distribusjonsparameteren

- Euler -nummer: E = 2.71828

- Sannsynligheten for å oppnå y = k er p

- k Det er antall suksesser 0, 1,2,3 ..

- n Det er antall tester eller hendelser (prøvestørrelse)

De diskrete tilfeldige variablene, som navnet tilsier, er avhengige av sjanse og tar bare diskrete verdier: 0, 1, 2, 3, 4 ..., k.

Gjennomsnittet av fordelingen er gitt av:

Σ -variansen, som måler spredningen av dataene, er en annen viktig parameter. For Poissons distribusjon er det:

σ = μ

Poisson bestemte at når n → ∞, og p → 0, kalt gjennomsnittet μ -også forventet verdi- Det har en tendens til en konstant:

μ → Konstant

Viktig: p Det er sannsynligheten for at forekomsten av hendelsen tar hensyn til den totale befolkningen, mens P (y) Det er Poissons spådom om prøven.

Modell og egenskaper

Poissons distribusjon har følgende egenskaper:

-Prøvestørrelsen er stor: N → ∞.

-Hendelsene eller hendelsene som vurderes er uavhengige av hverandre og forekommer tilfeldig.

-Sannsynlighet P For en viss hendelse og Det forekommer i en bestemt periode er veldig liten: P → 0.

-Sannsynligheten for mer enn en hendelse i tidsintervallet er 0.

-Gjennomsnittsverdien er nær en konstant gitt av: μ = n.P (n er prøvestørrelsen)

-Siden spredning σ er lik μ, ettersom den vedtar større verdier, er variabiliteten også større.

-Hendelsene må distribueres jevnt i tidsintervallet som brukes.

-Settet med mulige hendelsesverdier og Det er: 0,1,2,3,4 .. .

Kan tjene deg: tilfeldig eksperiment: konsept, prøveområde, eksempler

-Summen av Yo Variabler som følger en Poisson -distribusjon, er også en annen Poisson -variabel. Gjennomsnittsverdien er summen av gjennomsnittsverdiene for disse variablene.

Forskjeller med binomial distribusjon

Poissons distribusjon skiller seg fra binomial distribusjon i følgende viktige aspekter:

-Binomialfordelingen påvirkes både av størrelsen på S -prøven og av sannsynligheten P, Men Poissons distribusjon påvirkes bare av gjennomsnittet μ.

-I en binomial fordeling er de mulige verdiene for den tilfeldige variabelen og De er 0,1,2,…, i stedet i fordelingen av Poisson er det ingen øvre grense for disse verdiene.

Eksempler

Poisson anvendte opprinnelig sin berømte distribusjon på juridiske saker, men på industrielt nivå var en av dens første bruksområder i produksjonen av øl. I denne prosessen brukes gjærvekster til gjæring.

Gjæren består av levende celler, hvis populasjon er variabel i tid. I fremstilling av øl er det nødvendig å legge til nødvendig mengde, så det er nødvendig å kjenne mengden celler per volum enhet.

Under andre verdenskrig ble Poissons distribusjon brukt til å vite om tyskerne virkelig pekte mot London fra Calais, eller bare skyte tilfeldig. Dette var viktig for de allierte å bestemme hvor god det var teknologien som er tilgjengelig for nazistene.

Praktiske applikasjoner

Poissons distribusjonsapplikasjoner refererer alltid til tidstall eller romtelling. Og ettersom sannsynligheten for forekomst er liten, er den også kjent som "Law of Rare Events".

Her er en liste over hendelser som faller i en av disse kategoriene:

-Registrering av partikler i et radioaktivt forfall, som i likhet med veksten av gjærceller, er en eksponentiell funksjon.

-Antall besøk på et bestemt nettsted.

-Menneskers ankomst til en rad for å betale eller bli deltatt (teori om halene).

-Antall biler som går gjennom et visst punkt på en vei, for et gitt tidsintervall.

Figur 2. Mengden biler som går gjennom et punkt følger omtrent en Poisson -distribusjon. Kilde: Pixabay.

-Mutasjoner led i en viss DNA -kjede etter å ha mottatt eksponering for stråling.

-Diameter meteor nummer større enn 1 m falt i løpet av et år.

-Feil per kvadratmeter av et stoff.

-Mengde blodceller i 1 kubikk centimeter.

-Ringer per minutt til en telefonutveksling.

-Sjokolade gnister til stede i 1 kg kakedeig.

-Antall trær smittet forresten i 1 hektar skog.

Merk at disse tilfeldige variablene representerer antall ganger en hendelse skjer i en fast periode (Ringer per minutt til telefonutvekslingen), eller et gitt romområde (Defekter av et stoff per kvadratmeter).

Kan tjene deg: proporsjonal variasjon

Disse hendelsene, som allerede etablert, er uavhengige av tiden som har gått siden forrige forekomst.

Nærmer seg binomialfordelingen med fordelingen av Poisson

Poissons distribusjon er en god tilnærming til binomial distribusjon så lenge som:

-Prøvestørrelsen er stor: n ≥ 100

-Sannsynlighet P er liten: P ≤ 0,1

- μ være i rekkefølgen av: NP ≤ 10

I slike tilfeller er Poissons distribusjon et utmerket verktøy, siden binomial distribusjon kan bli komplisert å søke i disse tilfellene.

Løste øvelser

Oppgave 1

En seismologisk studie slo fast at det i løpet av de siste 100 årene var 93 store jordskjelv over hele verden, minst 6.0 på Richter -logaritmisk skala-. Anta at Poissons distribusjon er en tilstrekkelig modell i dette tilfellet. Finne:

a) Gjennomsnittlig forekomst av store jordskjelv per år.

b) Ja P (y) Det er sannsynligheten for å skje og Jordskjelv for et tilfeldig valgt år, finn følgende sannsynligheter:

P(0), P(1), P (2), P (3), P (4), P (5), P (6) og P (7).

c) De sanne resultatene av studien er som følger:

- 47 år (0 jordskjelv)

- 31 år (1 jordskjelv)

- 13 år (2 jordskjelv)

- 5 år (3 jordskjelv)

- 2 år (4 jordskjelv)

-  0 år (5 jordskjelv)

- 1 år (6 jordskjelv)

- 1 år (7 jordskjelv)

Hvordan er disse resultatene med de oppnådd i underavsnitt B? Er Poissons distribusjon et godt valg å modellere disse hendelsene?

Løsning på)

a) Jordskjelv er hendelser hvis sannsynlighet p Han er liten og vi vurderer en begrenset periode, på ett år. Det gjennomsnittlige jordskjelv er:

μ = 93 /100 jordskjelv / år = 0.93 jordskjelv per år.

Løsning B)

b) For å beregne de forespurte sannsynlighetene, erstattes verdier i formelen som er gitt i begynnelsen:

For eksempel å finne P (2), Noe som vil være sannsynligheten for at det vil være 2 store jordskjelv i året:

y = 2

μ = 0.93

E = 2.71828

Og dette er sannsynligheten for at det er 7 store jordskjelv i et år:

Det er ganske mindre enn P (2).

Resultatene er listet opp nedenfor:

P (0) = 0.395, P (1) = 0.367, P (2) = 0.171, P (3) = 0.0529, P (4) = 0.0123, P (5) = 0.00229, P (6) = 0.000355, P (7) = 0.0000471.

For eksempel kan vi si at det er sannsynlighet for 39.5 % at det ikke oppstår noe stort jordskjelv i et gitt år. Eller at det er 5,29 % som 3 store jordskjelv forekommer det året.

Løsning C)

c) Frekvensene blir analysert, multipliserer med n = 100 år:

39.5; 36.7; 17.1 ; 5.29; 1.23; 0.229; 0.0355 og 0.00471.

Kan tjene deg: algebraiske derivater

For eksempel:

- En frekvens på 39.5 indikerer at i 39.5 av 100 år eller store jordskjelv oppstår, kan vi si at det er ganske nær det virkelige 47 år gamle resultatet uten noe stort jordskjelv.

La oss sammenligne et annet Poisson -resultat med reelle resultater:

- Verdien oppnådd fra 36.7 betyr at det i en 37 -års periode er 1 flott jordskjelv. Det virkelige resultatet er at det i løpet av 31 år var en stor jordskjelv, et godt tilfeldighet med modellen.

- 17 forventes.1 år med 2 store jordskjelv og det er kjent at det i løpet av 13 år, som er en nær verdi, var i virkeligheten 2 store jordskjelv.

Derfor er Poisson -modellen akseptabel for denne saken.

Oppgave 2

Et selskap anslår at antall komponenter som mislykkes før de fullfører 100 timers drift, følger en Poisson -distribusjon. Hvis gjennomsnittlig antall feil er 8 på den tiden, finn følgende sannsynligheter:

a) at en komponent mislykkes på 25 timer.

b) Feil mindre enn to komponenter, på 50 timer.

c) at minst tre komponenter mislykkes på 125 timer.

Løsning på)

a) Det er kjent at den gjennomsnittlige feilen på 100 timer er 8, derfor forventes den fjerde delen av feil på 25 timer, det vil si 2 feil. Dette vil være parameteren μ.

Sannsynligheten for å mislykkes 1 komponent blir bedt om, den tilfeldige variabelen er "komponenter som mislykkes før 25 timer" og verdien er y = 1. Ved å erstatte sannsynlighetsfunksjonen:

 b) Nå er den tilfeldige variabelen "komponenter som mislykkes før 50 timer". Parameteren er μ = 4, Siden den forventede verdien av feil på 50 timer er 4.

Spørsmålet er imidlertid sannsynligheten for at mindre enn to komponenter mislykkes på 50 timer, ikke at nøyaktig 2 komponenter mislykkes på 50 timer, derfor må vi legge til sannsynlighetene som:

-Ingen mislykkes

-Mislykkes bare 1

P (mindre enn 2 komponenter) = P (0) + P (1)

P (mindre enn 2 komponenter) = 0.0183+0.0732 = 0.0915

c) at minst 3 komponenter mislykkes i 125, betyr det at 3, 4, 5 eller mer på den tiden kan mislykkes.

Sannsynligheten som oppstår minst en av flere hendelser er lik 1, bortsett fra sannsynligheten for at ingen av hendelsene vil skje.

-Hendelsen som søkes er å mislykkes 3 eller flere komponenter på 125 timer

-At hendelsen ikke skjer, betyr at mindre enn 3 komponenter mislykkes, hvis sannsynlighet er: P (0)+P (1)+P (2)

Μ -parameteren for distribusjonen i dette tilfellet er:

 μ = 8 + 2 = 10 feil på 125 timer.

P (Fallen 3 eller flere komponenter) = 1- P (0)- P (1)- P (2) =

= 1-0.0026786 = 0.9972

Referanser

1. Mathworks. Poisson distribusjon. Gjenopprettet fra: er.Mathworks.com
2. Mendenhall, w. 1981. Statistikk for administrasjon og økonomi. 3. utgave. IBEROAMERICA REDAKSJON GROUP.
3. Stat Trek. Lær deg selv statistikk. Poisson distribusjon. Gjenopprettet fra: Stattrek.com,
4. Triola, m. 2012. Elementær statistikk. 11. Ed. Pearson Education.
5. Wikipedia. Poisson distribusjon. Hentet fra: i.Wikipedia.org