Hva er et deterministisk eksperiment?

Han Deterministisk eksperiment, I statistikk er det en som har et forutsigbart og reproduserbart resultat så lenge de samme startbetingelsene og parametrene opprettholdes. Det vil si at årsak-virkning-forholdet er kjent i sin helhet.

For eksempel er tiden som tar sanden fra den ene klokken for å bevege seg fra det ene rommet til det andre et deterministisk eksperiment, fordi resultatet er forutsigbart og reproduserbart. Så lenge forholdene er de samme, vil det ta samme tid å flytte fra kapsel til kapsel.

Figur 1. Tiden som tar sanden fra det ene rommet til det andre er et deterministisk eksperiment. Kilde: Pixabay

Mange fysiske fenomener er deterministiske, noen eksempler er følgende:

- Et tettest gjenstand enn vann, som en stein, vil alltid synke.

- En flottør, som er mindre tett enn vannet, vil alltid være flytende (med mindre en kraft som holder den nedsenket) utøves).

- Koketemperaturen på vann ved havnivået er alltid 100 ºC.

- Tiden det tar å falle en gitt som synker fra hvile, siden den bestemmes av høyden den ble droppet fra og denne gangen er alltid den samme (når den frigjøres fra samme høyde).

Dra nytte av terningens eksempel. Hvis dette blir droppet, selv når du er nøye med å gi samme orientering og alltid i samme høyde, er det vanskelig å forutsi hvilket ansikt det vil dukke opp når den har stoppet på bakken. Dette ville være et tilfeldig eksperiment.

Teoretisk sett, hvis de var kjent med uendelige presisjonsdata som: posisjon; innledende hastighet og terningorientering; form (avrundede eller kantete kanter); og restitusjonskoeffisient av overflaten som den faller på, vil det kanskje være mulig å forutsi, gjennom komplekse beregninger, hvilket ansikt terningen vil vise når det stopper. Men enhver liten variasjon i startforholdene vil gi et annet resultat. 

Slike systemer er deterministiske og samtidig kaotiske, siden en liten endring av de opprinnelige forholdene endrer det endelige resultatet på en tilfeldig måte.

Kan tjene deg: System of Equations: Solution Methods, Eksempler, øvelser

[TOC]

Mål

De deterministiske eksperimentene er fullstendig målbare, men fortsatt er målingen av resultatet ikke uendelig presis og har en viss usikkerhetsmargin.

La oss sette for eksempel følgende eksperiment, helt deterministisk: Slipp en lekebil i en rett skråning.

Figur 2. En bil går ned gjennom en rettlinjet skråning i et deterministisk eksperiment. Kilde: Pixabay.

Det frigjøres alltid fra samme utgangspunkt, og pass på å ikke gi noen impuls. I dette tilfellet må tiden som tar bilen å reise banen alltid være den samme.

Nå har et barn tenkt å måle tiden han tar til vognturen sporet. For dette vil du bruke stoppeklokken som er integrert i mobiltelefonen din.

Å være observatør gutt, det første du bemerker er at måleinstrumentet ditt har en begrenset presisjon, fordi den minste tidsforskjell som kan måle stoppeklokken er 1 hundreled.

Så fortsetter barnet med å utføre eksperimentet og med mobilstoppeklokken på 11 ganger - la oss si at for å være sikker - tiden han tok til barnevognen for å reise det skrå flyet, og oppnå følgende resultater:

3.12s 3.09s 3.04s 3.04s 3.10s 3.08s 3.05s 3.10s 3.11s 3.06s og 3.03s.

Barnet er overrasket, for på skolen hadde de fortalt ham at dette er et deterministisk eksperiment, men i hver grad oppnådde han et litt annet resultat.

Variasjoner i den grad

Hva som kan være årsakene som i hver måling har et annet resultat? 

En årsak kan være nøyaktigheten til instrumentet, som det allerede var sagt er 0,01s. Men legg merke til at forskjellene i målingene er over den verdien, så det bør tenkes på andre årsaker, for eksempel:

- Små variasjoner av utgangspunktet.

- Forskjeller i begynnelsen og stoppet av stoppeklokken, på grunn av barnets reaksjonstid.

Når det gjelder reaksjonstiden, oppstår en forsinkelse absolutt siden barnet ser at vogna begynner å bevege seg, til stoppeklokken trykker. 

Kan tjene deg: kanter på en kube

På samme måte er det ved ankomst en forsinkelse på grunn av tid til reaksjon. Men start- og ankomstforsinkelser blir kompensert, slik at tiden som er oppnådd må være veldig nær den virkelige. 

I alle fall er kompensasjon for reaksjonsforsinkelse ikke nøyaktig, fordi reaksjonstidene kan ha små variasjoner i hver prøve, noe som forklarer forskjellene i resultatene.

Det som da er det sanne resultatet av eksperimentet?

Resultater av en måling og feil

For å rapportere det endelige resultatet må vi bruke statistikk. La oss først se hvor ofte resultatene gjentas:

- 3.03s (1 gang)

- 3.04s (2 ganger)

- 3.05s (1 gang)

- 3.06s (1 gang)

- 3.08s (1 gang)

- 3.09s 1 gang

- 3.10s (2 ganger)

- 3.11s (1 gang)

- 3.12s (1 gang)

Når vi bestiller dataene, innser vi at en mote eller mer gjentatt resultat. Da er resultatet for å rapportere det aritmetiske gjennomsnittet, som kan beregnes som følger:

(1 × 3,03 + 2 × 3,04 + 1 × 3,05 + 1x 3,06 + 1 × 3,08 + 1 × 3,09 + 2 × 3,10 + 1 × 3,11 + 1 × 3,12) / (1 + 2 + 1 + 1 + 1 + 1 + 2 + 1 + 1).

Resultatet av den forrige beregningen er 3.074545455. Logisk sett gir det ingen mening å rapportere alle disse desimalene i resultatet, fordi hver måling ikke har noe pluss 2 presisjonsdesimaler. 

Ved å bruke avrundingsreglene kan det sies at tiden det tar til vognturen. Sporet er det avrundede aritmetiske gjennomsnittet til to desimaler.

Resultatet vi kan rapportere for eksperimentet vårt er:

3.08 sekunder er tiden du tar til lekebilen, og slår det skrånende sporet.

- Målefeil

Som vi ser i vårt eksempel på et deterministisk eksperiment, har hver måling en feil, siden det ikke kan måles med uendelig presisjon.

I alle fall er det eneste som kan gjøres å forbedre instrumenter og målemetoder for å oppnå et mer presist resultat.

I forrige seksjon ga vi et resultat for vårt deterministiske eksperiment av tiden det tar til lekebilen å reise et skråbane. Men dette resultatet innebærer en feil. Nå vil vi forklare hvordan du beregner den feilen.

Det kan tjene deg: Rektangulære koordinater: Eksempler og øvelser løst

- Målefeilberegning

I målingene for tid er det en spredning i tiltakene som er gjort. De standardavvik Det er en ofte brukt statistisk form for å rapportere datatispersjon. 

Varians og standardavvik

Måten å beregne standardavviket er slik: Først er variansen av dataene, definert på denne måten:

Summen av forskjellene i hvert resultat med det aritmetiske gjennomsnittet, kvadratet og delt på det totale antallet data

Hvis kvadratroten tas til variansen, oppnås standardavviket.

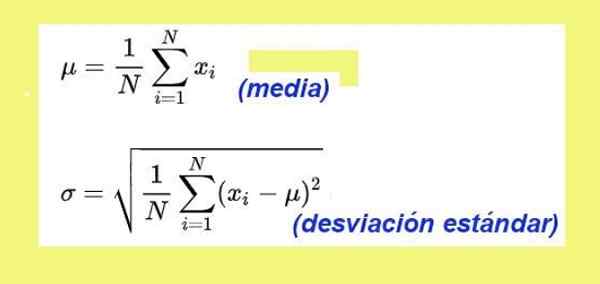Figur 3. Gjennomsnittlige formler og standardavvik. Kilde: Wikimedia Commons.

Standardavviket for nedstigningstidsdataene til leketøys auton er:

σ = 0,03

Resultatet ble avrundet til 2 desimaler, fordi presisjonen til hver av dataene er 2 desimaler. I dette tilfellet representerer 0,03s den statistiske feilen til hver av dataene.

Imidlertid har det gjennomsnittlige aritmetiske gjennomsnittet av de oppnådde tider en lavere feil. Gjennomsnittlig feil beregnes ved å dele standardavviket mellom kvadratroten til det totale datatummeret.

Gjennomsnittlig feil = σ / √n = 0,03 / √11 = 0,01

Det vil si at den statistiske feilen for gjennomsnittlig tid er 1 hundreledig sekund, og i dette eksemplet sammenfaller den med takknemligheten av stoppeklokken, men det er ikke alltid slik.

Som et endelig resultat av tiltaket rapporteres det da:

 T = 3,08s ± 0,01s er tiden det tar til lekebilen å reise det skrå sporet.

Det konkluderes med at selv når det gjelder et deterministisk eksperiment, har resultatet av måling ingen uendelig presisjon og alltid har en feilmargin. 

Og i tillegg, for å rapportere det endelige resultatet, er det nødvendig, selv når det gjelder et deterministisk eksperiment, bruk statistiske metoder.

Referanser

1. Canalphi. Deterministisk eksperiment. Gjenopprettet fra: YouTube.com
2. Mathemovil. Deterministisk eksperiment. Gjenopprettet fra: YouTube.com
3. Pishro Nick h . Introduksjon til sannsynlighet. Hentet fra: sannsynlighetskurs.com
4. Ross. Sannsynlighet og statistikk for ingeniører. Mc-Graw Hill.
5. Statistikk hvordan. Deterministisk: Definisjon og eksamener. Gjenopprettet fra: StatisticShowto.Datascienceceral.com
6. Wikipedia. Typisk avvik. Gjenopprettet fra: er.Wikipedia.com
7. Wikipedia. Eksperiment (sannsynlighetsteori). Hentet fra: i.Wikipedia.com