Korrelasjonskoeffisientformler, beregning, tolkning, eksempel

Han korrelasjonskoeffisient I statistikk er det en indikator som måler trenden med to kvantitative variabler x og y for å ha et forhold mellom linearitet eller proporsjonalitet mellom dem.

Generelt er parene med variabler x og y to egenskaper for samme populasjon. For eksempel kan x være høyden på en person e og dens vekt.

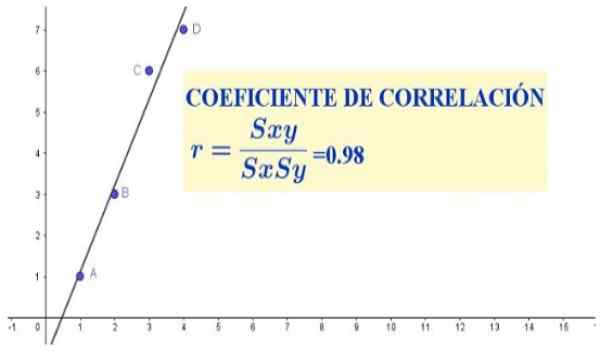
Figur 1. Korrelasjonskoeffisient for fire datapar (x, y). Kilde: f. Zapata.

I dette tilfellet vil korrelasjonskoeffisienten indikere om det er et forhold mellom proporsjonaliteten mellom høyden og vekten til en gitt populasjon eller ikke.

Pearsons lineære korrelasjonskoeffisient er betegnet med bokstaven r Små og den minste og maksimale verdier er henholdsvis -1 og +1. 

En verdi r = +1 skulle indikere at hele par (x, y) er perfekt justert og at når x vokser, og vil vokse i samme andel. På den annen side, hvis det skjer at r = -1, ville settet med par også være perfekt på linje, men i så fall når X vokser, og avtar i samme andel.

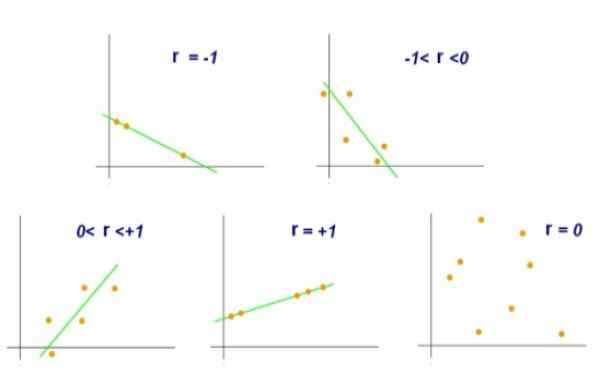Figur 2. Ulike verdier av den lineære korrelasjonskoeffisienten. Kilde: Wikimedia Commons.

På den annen side vil en verdi r = 0 indikere at det ikke er noen lineær korrelasjon mellom variablene x og y. Mens en verdi på r = +0,8 ville indikere at parene (x, y) har en tendens til å gruppere seg til den ene siden og en annen av en viss linje.

Formelen for beregning av korrelasjonskoeffisienten R er som følger:

Der telleren representerer samvariasjonen mellom variablene x og y, mens nevneren er produktet av standardavviket for variabel x og standardavviket for variabelen og.

Hvordan beregne korrelasjonskoeffisienten?

Den lineære korrelasjonskoeffisienten er en statistisk mengde som er integrert i vitenskapelige kalkulatorer, i de fleste regneark og statistiske programmer.

Kan tjene deg: Hyperbolsk paraboloid: Definisjon, egenskaper og eksempler

Imidlertid er det praktisk å vite hvordan formelen som definerer den brukes, og for dette vil en detaljert beregning vises, utført på et lite datasett.

Og som fremgått i forrige seksjon, er korrelasjonskoeffisienten SXY -samvariasjonen delt på produktet av standardavviket SX for variablene x og SY for variabelen og.

Samvariasjon og varians

SXY -samvariasjonen er:

Sxy = [σ (xi -) (yi -)] / (n -1)

Hvor summen går fra 1 til n par (xi, yi). E er henholdsvis de aritmetiske strømpene til dataene.

For sin del er standardavviket for variabel x kvadratroten av variansen til XI -datasettet, med i fra 1 til n:

Sx = √ [σ (xi -)^2) / (n -1)]

Tilsvarende er standardavviket for variabelen og er kvadratroten til variansen til Yi -datasettet, med i fra 1 til n:

Sy = √ [σ (yi -)² ) / (N-1)]

Illustrerende sak

For å vise i detalj hvordan vi skal beregne korrelasjonskoeffisienten, vil vi ta følgende sett med fire par data 

(X, y): (1, 1); (23); (3, 6) og (4, 7).

Først beregner vi det aritmetiske gjennomsnittet for x og y, som følger:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Deretter beregnes de gjenværende parametrene:

SXY COVARIANCE

Sxy = [(1 - 2.5) (1 - 4.25) + (2 - 2.5) (3 - 4.25) + (3 - 2.5) (6 - 4.25) +.. ... .(4 - 2.5) (7 - 4.25)] / (4-1)

Sxy = [(-1.5) (-3.25) + (-0.5) (-1.25) + (0.5) (1.75) +.. . 

Kan tjene deg: avledningsregler (med eksempler)

.. .(1.5) (2.75)] / (3) = 10.5/3 = 3.5

Standardavvik sx

Sx = √ [(-1.5)² + (-0.5)² + (0.5)² + (1.5)²) / (4-1)] = √ [5/3] = 1.29

Standardavvik SY

Sx = √ [(-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (4-1)] = 

√ [22.75/3] = 2.75

Rekkverkskoeffisient r

R = 3.5 / (1.29 * 2.75) = 0.98

Tolkning

I datasettet til det forrige tilfellet er det en sterk lineær sammenheng mellom variablene x og y, som manifesterer både i spredningsgrafen (som kan sees i figur 1) og i korrelasjonskoeffisienten, som kastet en verdi ganske nær enheten.

I den grad korrelasjonskoeffisienten er nærmere 1 eller -1, gjør mer fornuft innstillingen av dataene til en linje, resultatet av den lineære regresjonen.

Lineær regresjon

Den lineære regresjonslinjen er oppnådd fra Metode for minste firkanter. der regresjonslinjeparameteren oppnås fra minimering av summen av kvadratet for forskjellen mellom verdien og estimert og YI for N -dataene.

På den annen side er parametere A og B på regresjonslinjen y = a + bx, oppnådd ved metoden for minimumsplasser,:

*B = sxy / (sx²) For skråningen

*A = - b for skjæringspunktet mellom regresjonslinjen med aksen til og og.

Husk at SXY er samvariasjonen definert ovenfor og SX² Det er variansen eller kvadratet med standardavviket som tidligere er definert. E er de aritmetiske middelene til dataene x og og og henholdsvis.

Eksempel

Korrelasjonskoeffisienten brukes til å avgjøre om det er en lineær type korrelasjon mellom to variabler. Det er aktuelt når variablene som skal studeres er kvantitative, og de skal også følge en normal type distribusjon.

Kan tjene deg: korrespondanse regel om en funksjon

Et illustrerende eksempel vi har nedenfor: et mål på graden av overvekt er kroppsmasseindeksen, som oppnås ved å dele vekten til en person i kilo mellom høyden på det samme i firkantede enheter til torget.

Det er ønsket å vite om det er en sterk sammenheng mellom kroppsmasseindeksen og konsentrasjonen av HDL -kolesterol i blod, målt i millimoler per liter. For dette formål har en studie blitt gjort med 533 personer oppsummert i den følgende grafen, der hvert punkt representerer en persons data.

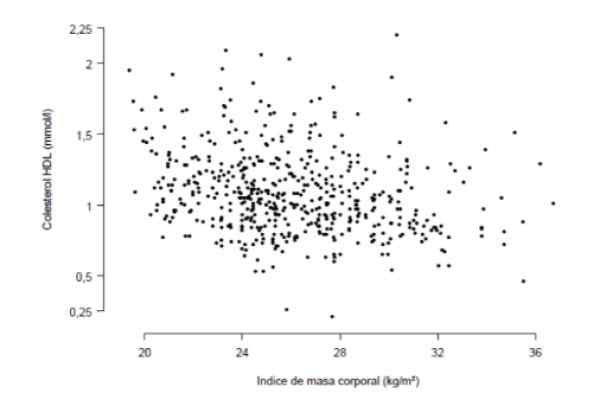Figur 3. IMC -studie og HDL -kolesterol hos 533 pasienter. Kilde: Aragonese Institute of Health Sciences (IACS).

Fra den nøye observasjonen av grafen følger det at det er en viss lineær (ikke veldig merket) trend mellom HDL -kolesterolkonsentrasjonen og kroppsmasseindeksen. Det kvantitative målet på denne trenden er korrelasjonskoeffisienten som for dette tilfellet viste seg å være r = -0,276.

Referanser

1. González c. Generell statistikk. Gjenopprettet fra: Tarwi.La Molina.Edu.PE
2. IACS. Aragonese Institute of Health Sciences. Hentet fra: ICS-Aagon.com 
3. Salazar c. og Castillo s. Grunnleggende statistikkprinsipper. (2018). Hentet fra: DSPACE.Uce.Edu.Ec
4. Superprof. Korrelasjonskoeffisient. Gjenopprettet fra: Superprof.er
5. USAC. Beskrivende statistikkhåndbok. (2011). Gjenopprettet fra: Statistikk.Ingeniørfag.USAC.Edu.Gt
6. Wikipedia. Pearson korrelasjonskoeffisient. Gjenopprettet fra: er.Wikipedia.com.