Generell kultur og samfunn

Eksponentiell distribusjon

4972
1590
Markus Fredriksen

Vi forklarer hva som er eksponentiell fordeling, dens egenskaper, formler, eksempler og satte løse øvelser

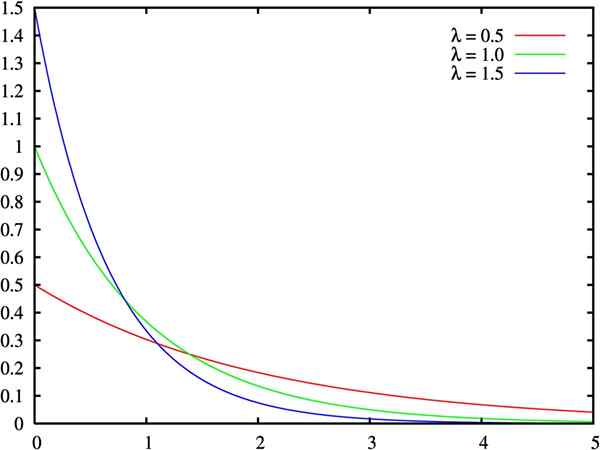
Graf over tetthetsfunksjonen til eksponentiell fordeling, for tre verdier av lambda -parameteren. Kilde: Wikimedia Commons.

Hva er eksponentiell distribusjon?

De Eksponentiell distribusjon Det er en sannsynlig modell for kontinuerlige tilfeldige variabler. Dette betyr at du gjennom det kan vite sannsynligheten for forekomst av en viss verdi av variabelen, så det er en sannsynlighetsfordeling.

For å oppnå distribusjonen starter den fra en Tetthetsfunksjon, som har en eksponentiell form av parameter λ> 0:

$f(x)=\begincases \lambda e^-\lambda x& \text si x>0 \\ 0 og \ tekst Ja x \ leq 0 \ Slutt tilfeller$

Tetthetsfunksjonen som sådan tillater ikke beregning av sannsynligheten, men når den er etablert f (x), oppnås distribusjonsfunksjonen f (x), som sannsynlighetene oppnås, oppnås ved integrering av F (x). For eksempel er sannsynligheten for at den tilfeldige variabelen tar verdier mellom 0 og X:

$F(x)=P[x\leq x]=\int_0^xf(x)dx$

Å gjennomføre integrasjonen, som er veldig enkel, siden integralen av en eksponentiell er den samme eksponentielle, bortsett fra konstantene som følger med argumentet, oppnås det:

$F(x)=\int_0^x\lambda e^-\lambda xdx=\lambda \left (-\frac1\lambda \right )\left [ e^-\lambda x \right ]_0^x=-\left (e^-\lambda x-e^0 \right )=1-e^-\lambda x$

Eksponentiell distribusjon er mye brukt for å bestemme sannsynligheten for en hendelse etter en viss ventetid, for eksempel tiden som finner sted i fremveksten av et sykehus før en pasient kommer.

Ofte refererer hendelser til feil eller nedbrytning av elektriske, elektroniske og andre typer. I dette tilfellet hjelper eksponentiell distribusjon å estimere tiden det tar for en komponent å mislykkes, og også tiden mellom reparasjoner. Dette er kjent som pålitelighetsteori.

Kjennetegn på eksponentiell distribusjon

Noen av de mest fremragende funksjonene i tetthetsfunksjonen f (x) i eksponentiell distribusjon er følgende:

f (x) er positivt.
Området under kurven y = f (x) = λe^−λ^x Det er alltid lik 1, fordi summen av sannsynligheten for forekomst av alle verdiene på variabelen må være 1. Dette er en betingelse som tetthetsfunksjoner oppfyller. Dette området beregnes gjennom integralen:

Kan tjene deg: Anuma

$\int_-\infty ^\infty f(x)dx=\int_-\infty ^\infty \lambda e^-\lambda xdx=1$

Mangel på eksponentiell distribusjonsminne

Det mest enestående trekk ved eksponentiell distribusjon er mangelen på minne. Anta for eksempel at tiden går.

Vel, mangelen på minne refererer til å vite at elementet fungerte for en "s" overlevelsestid, ikke endrer sannsynligheten for at elementet vil fortsette å løpe opp til en viss ekstra tid "t".

Det vil si at sannsynligheten for at elementet mislykkes herfra til en viss tid (1 minutt, 1 time, for eksempel) ikke er avhengig av å ha fungert bra så langt.

Matematisk beregnes det etter definisjon av sannsynlighet for uavhengige hendelser:

$P[x\geq s+t/x\geq s]=\fracP[x\geq s+t]P[x\geq s]=\frac1-F(s+t)1-F(s)=\frac1- [1-e^-\lambda (s+t) ]1- [1-e^-\lambda s ]= \beginmatrix \\ \endmatrix$

$=e^-\lambda t$

Derfor avhenger ikke sannsynligheten av s eller overlevelsestid.

Formler

1.- Tetthetsfunksjonen til eksponentiell fordeling er:

$f(x)=\begincases \lambda e^-\lambda x& \text si x>0 \\ 0 og \ tekst Ja x \ leq 0 \ Slutt tilfeller$

Hvor λ er distribusjonsparameteren.

2.- Som beskrevet ovenfor, er fordelingen av sannsynlighetene i seg selv betegnet som F (x) og de forskjellige sannsynlighetene oppnås ved integrering av tetthetsfunksjonen:

$F(x)=\begincases 0 & \text si x\leq 0 \\ 1-e^-\lambda x& \text si x>0 \ Slutt tilfeller$

3.- Fra det ovennevnte følger det at sannsynligheten for at variabelen tar verdier mindre enn eller lik “x” er p [x≤x] = 1 −E^−λ^x.

4.- Området under kurven y = f (x), inkludert mellom A og B, gjør det mulig å beregne sannsynligheten for at variabelen er i intervallet [a, b]. Dette området er:

P [a ≤ x ≤ b] = f (b) - f (a)

5.- Verdien av P [x ≥ a] er 1 - f (a) = 1 - (1 - e^−λ^x) = e^−λ^x

Forventet verdi av eksponentiell distribusjon

Håpet eller forventet verdi E (x) for eksponentiell fordeling er verdien som forventes å skje oftere. Det beregnes ut fra integralen:

Kan tjene deg: Informasjonsregistreringsteknikker

$E(x)=\int_0^\infty xf(x)dx$ Som lett løses med integrasjonsmetode av deler. Resultatet er:

E (x) = 1/λ

Varians av eksponentiell distribusjon

For beregning av variansen må integralen bestemmes:

$Var(x)=\int_0^\infty x^2f(x)dx$

Som også er løst med metoden for integrering av deler, for å oppnå:

Var (x) = 1/λ²

En egenart med eksponentiell fordeling er at standardavviket s (x), definert som kvadratroten til variansen er:

S (x) = √var (x) = √ (1/λ²) = 1/λ

Det vil si at standardavviket er lik håp om distribusjon.

Eksempler på eksponentiell distribusjon

Datasjon av karbonprøver 14

Eksponentiell fordeling brukes til å bestemme tiden det tar for å gå i oppløsning en radioaktiv partikkel. Disse tider brukes til å date fossile prøver ved radiokarbon.

Tid det tar å sjekke posten

Du kan modellere tiden brukerne tar for å gjennomgå e -posten deres, når varselet er mottatt, gjennom en eksponentiell distribusjon. Anta at distribusjonsparameteren er λ = 0.2, da, sannsynligheten for at en person tar mindre enn 1 minutt å gjennomgå e -posten hans er:

$P[x\leq 1]=\int_0^1f(x)dx=\int_0^10.2e^-0.2xdx$

Dette integralet ble løst i begynnelsen, det gjenstår bare å erstatte de numeriske verdiene i løsningen og beregne det endelige resultatet:

P [x ≤ 1] = 1 -E^-^0.2^×¹ = 1− e^-^0.2 = 1− 0.819 = 0.181

Den kan også erstattes direkte på f (x) funksjon gitt ovenfor, for å oppnå f (1).

Øvelser

Oppgave 1

Finn sannsynligheten for at en person senere en time gjennomgår e -posten sin, hvis sannsynlighetsfordelingen er eksponentiell, med parameter λ = 0.2.

Løsning

P [x ≥ 60] må beregnes, siden 1 time tilsvarer 60 minutter og sannsynligheten for at personen sent 60 minutter eller mer for å sjekke posten blir bedt om. Sannsynligheten beregnes med samme integral som ble presentert i begynnelsen, bare å endre integrasjonsgrensene:

Kan tjene deg: Rapa Nui: Historie, egenskaper, kultur, tradisjoner

$P[x\geq 60]=\int_60^\infty 0.2e^-0.2xdx=-\left ( -e^-0.2\times 60 \right )=0.000006144$

Verdien som er oppnådd er liten, så det er veldig usannsynlig at en person tar mer enn en time å gjennomgå e -posten deres.

Oppgave 2

De elektriske pærene har vanligvis en endelig varighet, bortsett fra den berømte pæren av brannstasjonen i Livermore, California, som aldri har mislyktes siden den var på for første gang, i 1901.

Anta at varigheten av en strømpære følger en eksponentiell distribusjon, med en forventet verdi på 8 måneder. Regne ut:

a) Hva er sannsynligheten for at pæren vil vare mellom 5 og 14 måneder?

b) Sannsynligheten for at pæren vil vare mer enn 25 måneder, vel vitende om at den har mer enn 11 måneder i drift.

Løsning på

Den første tingen er å finne verdien av λ, gjennom den forventede verdien av distribusjonen e (x) = 8 måneder. I henhold til det som ble sagt i foregående avsnitt, er den forventede verdien det inverse av λ -parameteren, derfor:

E (x) = 1 /λ → λ = 1 /e (x) = 1/8 = 0.125

Deretter beregnes den forespurte sannsynligheten, ved hjelp av integralen som er gitt i begynnelsen, men enkelt å endre integrasjonsgrensene:

Deretter erstattes den i F (x) -funksjonen gitt i foregående avsnitt, som følger:

P [5 ≤ x ≤ 14] = F (14) - F (5) = [1 - E^{-(0.125 × 14)}] - [1 - e^{-(0.125 × 5)}] = 0.36

Løsning b

For å svare på dette problemet, vil egenskapen til mangelen på minne bli brukt, uttales ovenfor. Som det er kjent at det allerede har vart mer enn 11 måneder, da:

S = 11 måneder

Den ekstra tiden til å vare 25 måneder eller mer er:

T = 14 måneder

P [x ≥ s + t│t ≥ s] = p [x ≥ 11 + 14│t ≥ 11] = e^{−0.125 × 14}= 0.174