Syntetisk inndeling

Vi forklarer hva syntetisk inndeling er, en metode for å gjøre det, eksempler og øvelser løst.

Hva er syntetisk inndeling?

De Syntetisk inndeling Det er en enkel måte å dele et polynom P (x) med en av formen d (x) = x - c - c. For eksempel polynom P (x) = (x⁵+3x⁴-7x³+2x²-8x+1) Det kan representeres som multiplikasjon av de to enkleste polynomene (x+1) og (x⁴ + 2x³).

Det er et veldig nyttig verktøy, siden det, i tillegg til å la oss dele polynomer, også tillate å evaluere et P (x) polynom i et hvilket Polynom.

Takket være divisjonsalgoritmen, vet vi at hvis vi har to P (x) og d (x) polynom (x) + r (x), hvor r (x) er null eller er mindre enn q (x). Disse polynomene er kjent som henholdsvis kvotient og rest eller hvile.

I de anledninger der polynom d (x) er av X - C -formen, gir den syntetiske inndelingen oss en kort måte å finne hvem som er q (x) og r (x).

Syntetisk divisjonsmetode

La P (x) = a_nxⁿ+til_N-1x^N-1+… +A₁x+a₀ Polynomet vi ønsker å dele og d (x) = x-c divisoren. For å dele ut med den syntetiske divisjonsmetoden fortsetter vi som følger:

1- Vi skriver koeffisientene til P (x) i første rad. Hvis noen X -effekt ikke vises, plasserer vi null som koeffisient.

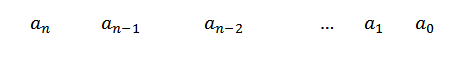
2- I andre rad, til venstre for en_n Vi plasserer C og tegner divisjonslinjer, som vist i følgende figur:

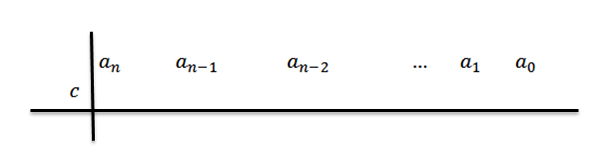
3- Vi senker den ledende koeffisienten til tredje rad.

Kan tjene deg: Euler -metode: Hva er bruk av prosedyre og øvelser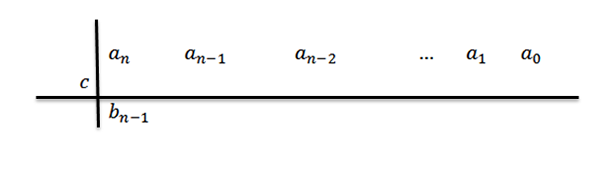

I dette uttrykket B_N-1= a_n

4- Vi multipliserer C med den ledende koeffisienten B_N-1 Og vi skriver resultatet i den andre raden, men en kolonne til høyre.

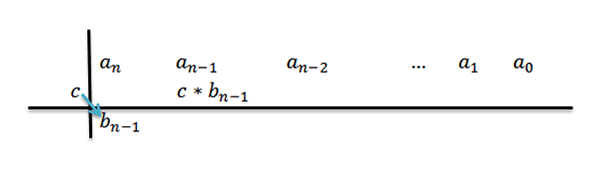
5- Vi legger til kolonnen der vi skriver det forrige resultatet og resultatet er plassert under nevnte sum. Det vil si i samme kolonne, tredje rad.

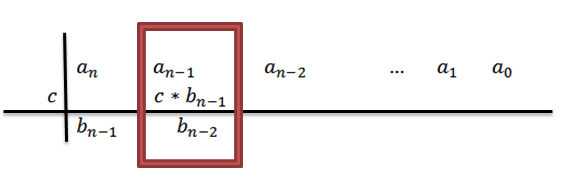
Ved å legge til, har vi som et resultat_N-1+C*b_N-1, som for komfort vil vi kalle B_N-2

6- Vi multipliserer C med forrige resultat og skriver resultatet til din rett i andre rad.

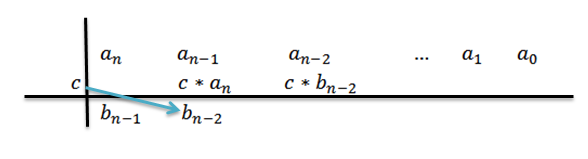
7- Vi gjentar trinn 5 og 6 til vi når koeffisienten til₀.

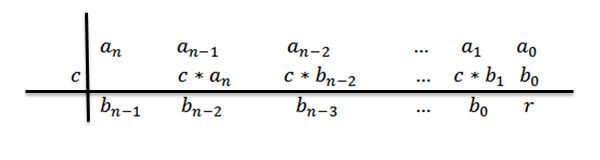
8- Vi skriver svaret, det vil si kvotienten og resten. Når vi driver inndeling av en grad N-polynom mellom et polynom i grad 1, har vi at kvotienten vil være grad N-1.

Koeffisientene til kvotientpolynomet vil være tallene på den tredje raden, bortsett fra den siste, som vil være restpolynomet eller resten av divisjonen.

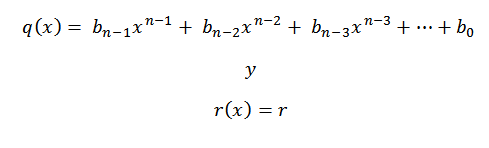
Løste øvelser

Eksempel 1

Gjør følgende divisjon etter syntetisk divisjonsmetode:

(x⁵+3x⁴-7x³+2x²-8x+1): (x+1).

Løsning

Først skriver vi utbyttekoeffisientene som følger:

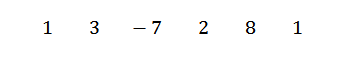
Så skriver vi C på venstre side, i andre rad, sammen med divisjonslinjene. I dette eksemplet C = -1.

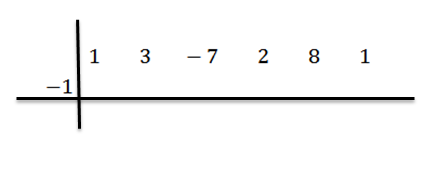
Vi senker den ledende koeffisienten (i dette tilfellet B_N-1 = 1) Og vi multipliserer det med -1:

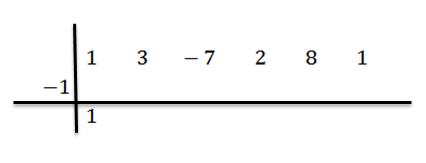
Vi skrev resultatet til høyre i den andre raden, som vist nedenfor:

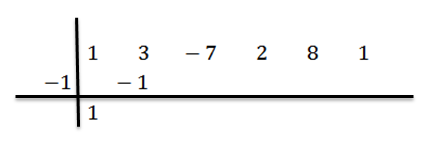
Vi legger til tallene i den andre kolonnen:

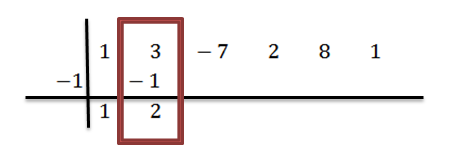
Vi multipliserer 2 med -1 og skriver resultatet i den tredje kolonnen, andre rad:

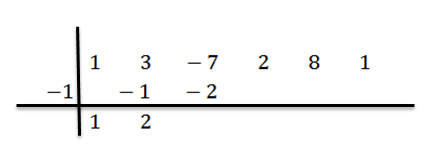
Vi legger til i den tredje kolonnen:

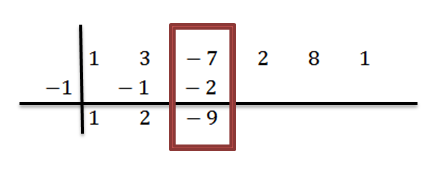
Vi fortsetter analogt til vi når den siste kolonnen:

Kan tjene deg: standard og overflødig tilnærming: Hva er og eksempler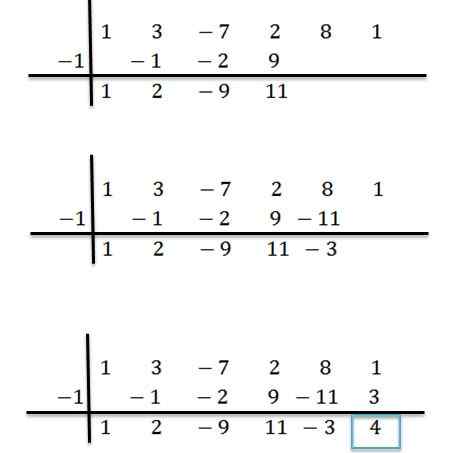

Dermed har vi at det siste antallet som er oppnådd er resten av divisjonen, og de gjenværende tallene er koeffisientene til kvotientpolynomet. Dette er skrevet som følger:

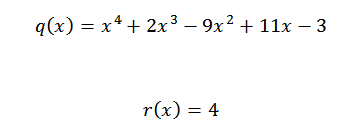
Hvis vi ønsker å bekrefte at resultatet er riktig, er det nok til å bekrefte at følgende ligning er oppfylt:

P (x) = q (x)*d (x) + r (x)

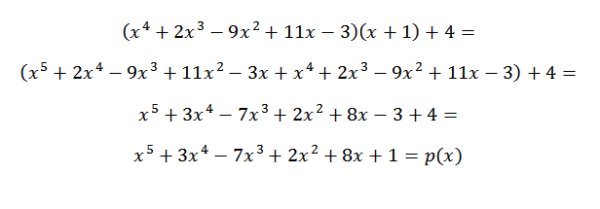
Dermed kan vi bekrefte at resultatet som er oppnådd er riktig.

Eksempel 2

Utfør følgende polynomavdeling etter syntetisk inndelingsmetode:

(7x³-x+2): (x+2)

Løsning

I dette tilfellet har vi at begrepet x² Det vises ikke, så vi vil skrive til 0 som koeffisient. Dermed ville polynomet forbli som 7x³+0x²-x+2.

Vi skriver koeffisientene dine på rad, det vil si:

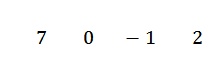
Vi skriver verdien av C = -2 til venstre på den andre raden og tegner divisjonslinjene.

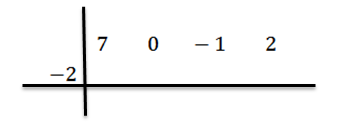
Vi senker den ledende koeffisienten B_N-1 = 7 og vi multipliserer det med -2, og skriver resultatet i den andre raden til høyre.

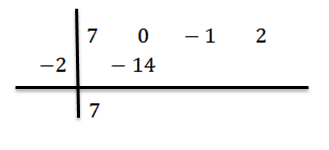
Vi legger til og fortsetter, som tidligere forklart, til vi når siste periode:

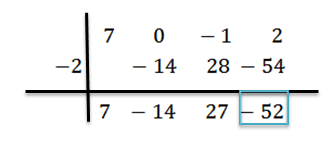
I dette tilfellet er resten r (x) = -52 og den oppnådde kvotienten er q (x) = 7x²-14x+27.

Eksempel 3

En annen måte å bruke syntetisk inndeling på er som følg.

For divisjonsalgoritmen kan vi skrive P (x) polynomet som følger:

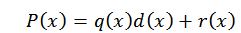
I dette uttrykket er henholdsvis Q (x) og r (x). Hvis d (x) = x-c, når vi evaluerer i C i polynom, finner vi følgende:

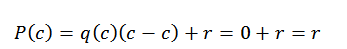
Dette er grunnen til at det bare gjenstår å finne R (x), og vi kan gjøre dette takket være den syntetiske divisjonen.

For eksempel har vi polynom P (x) = x⁷-9x⁶+19x⁵+12x⁴-3x³+19x²-37x-37 og vi vil vite hva verdien er når vi evaluerer den til x = 5. For dette utfører vi divisjonen mellom P (x) og d (x) = x -5 ved den syntetiske divisjonsmetoden:

Kan tjene deg: aksial symmetri: egenskaper, eksempler og øvelser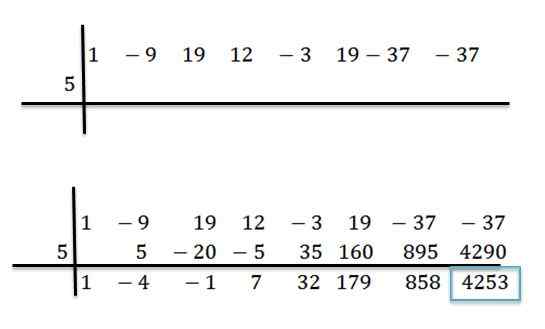

Når operasjonene er utført, vet vi at vi kan skrive P (x) som følger:

P (x) = (x⁶-4x⁵ -x⁴+ 7x³ +32x² +179x + 858)*(X-5) + 4253

Derfor, når vi evaluerer det, må vi:

P (5) = (5-4 (5) -5 +7 (5) +32 (5) +179 (5) +858)*(5-5) +4253

P (5) = (5-4 (5) -5 +7 (5) +32 (5) +179 (5) +858)*(0) +4253

P (5) = 0 + 4253 = 4253

Som vi kan se, er det mulig å bruke den syntetiske inndelingen for å finne verdien av et polynom når du evaluerer den i C i stedet for bare å erstatte C med x. 

Hvis vi prøver å evaluere P (5) på tradisjonell måte, vil vi ha behov for noen beregninger som vanligvis blir kjedelige.

Eksempel 4

Divisjonsalgoritmen for polynomer blir også oppfylt for polynomer med komplekse koeffisienter, og som en konsekvens har vi at den syntetiske inndelingsmetoden også fungerer for disse polynomene. Deretter vil vi se et eksempel.

Vi vil bruke den syntetiske divisjonsmetoden for å vise at z = 1+ 2i er en null av polynomet P (x) = x³+ (1+i) x² -(1+2i) x+(15+5i). Det vil si at resten av divisjonen p (x) mellom d (x) = x - z er lik null.

Vi fortsetter som før: I første rad skriver vi koeffisientene til P (x), deretter i det andre vi skriver Z og tegner divisjonslinjene.

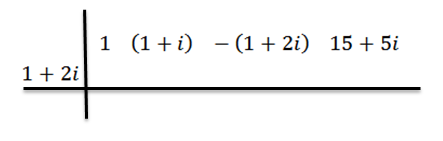
Vi gjør divisjonen som før, det vil si:

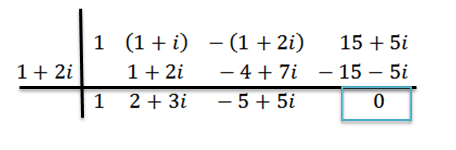
Vi kan se at resten er null; Derfor konkluderer vi med at z = 1+ 2i er en null P (x).

Referanser

1. Baldor, Aurelio. Algebra. Patria redaksjonell gruppe.
2. Demana, Waits, Foley & Kennedy. Precáculo: grafisk, numerisk, algebraisk. Pearson Education.