120 Divisors

De 120 Divisors De er alle de tallene som deler det nøyaktig. Disse tallene er som følger:

Divisorer på 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 30, 40, 60, 120

Også motsetningene til dette settet med tall, det vil si negativene, er 120 delinger, siden divisjonen er nøyaktig. 120 har 16 positive hele divisorer og mange andre negativer.

Det er flere måter å finne delingene av et tall. Hvis dette ikke er veldig stort, kan du bruke multiplikasjonstabellene (for tall mindre enn 100) og verifisere i hvilke tabeller det aktuelle antallet vises. For eksempel vises 12 i tabellene til 2, 3, 4 og 6, og dette er deres delere, sammen med 1 og de samme 12.

Antallet kan også deles inn i de viktigste faktorene, anvende delbarhetsreglene og multiplisere faktorene. Men du må være forsiktig med å ikke passere noen oversett.

Ettersom 120 er større enn 100, er det ikke direkte i multiplikasjonstabellene, men det er ikke for arbeidskrevende å finne sine 16. En gyldig prosedyre for alle tall vises umiddelbart, ved bruk av veldig enkle tabeller.

Hvor mange deling er 120?

For det første blir antallet deling av 120 funnet ut. Det er en formel som lar deg vite hvor mange du har, selv om den ikke sier hva de er.

Sammensatte tall, for eksempel 120, kan uttrykkes som produktet av primtall, eller krefter til disse. Ringer n til et hvilket som helst sammensatt nummer:

N = aⁿ ∙ b^m ∙ c^p ... r^k

Kan tjene deg: proporsjonalitetsrelasjoner: konsept, eksempler og øvelser

Tallene A, B, C ... r er primtall, og verdiene til n, m, p, ... k, de respektive kreftene. Nedbrytningen i primefaktorer på 120 er som følger:

120 | 2
60 | 2
30 | 2
15 | 3
5 | 5
1 | 1

På denne måten er 120 produktet av faktorene:

120 = 2³ ∙ 3 ∙ 5

Formel for beregning av antall delinger av n

Antall divisorer = (n +1) × (m +1) × (p +1) ... × (k +1)

Nå brukes formelen til 120. Fra nedbrytning i faktorer må du:

n = 3 (er kraften til 2)

M = 1 (de 3 er forhøyet til 1: 3¹ = 3)

P = 1 (de 5 virker også forhøyet til 1)

Med disse verdiene:

Antall divisorer på 120 = (3 +1) × (1 +1) × (1 +1) = 4 × 2 × 2 = 16

Dette resultatet sammenfaller med begynnelsen av begynnelsen: 120 har 16 delinger. I tillegg er det allerede kjent at 2, 3 og 5 er deling av 120, så vel som 10, siden et hvilket som helst antall som er ferdige i 0 er delbar med 10. Prosedyren for å finne dem alle vises umiddelbart.

Beregning av delingene på 120

Det gjøres ved hjelp av faktorene beregnet i forrige avsnitt. Der ble det sett at 2 er en hovedfaktor med eksponent 3, og 3 er en annen fetterfaktor, med eksponent 1. Med denne informasjonen er følgende tabell bygget:

Merk at kreftene til 2 begynner i 2⁰ og slutter i 2³, som er faktoren som oppstår når du nedbryter 120. Husk at 2⁰ og 3⁰ Begge er lik 1 (et hvilket som helst tall som er høyt til 0 er 1). For faktor 3 starter det i 3⁰ Til 3¹, siden 3¹ = 3.

Deretter fullføres tabellen med produktet av tallene i rødt, som vist her:

Kan tjene deg: Multiplikativ omvendt: Forklaring, eksempler, løste øvelser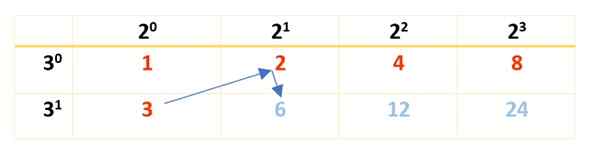

Alle røde og blå tall er 120 delinger, men det er knapt 8. For å finne de gjenværende er et nytt bord sprengt, delingene som allerede er oppnådd i første rad, og faktoren som gjenstår å ta hensyn til er skrevet: 5, med kreftene i den første kolonnen, til venstre, som dette:

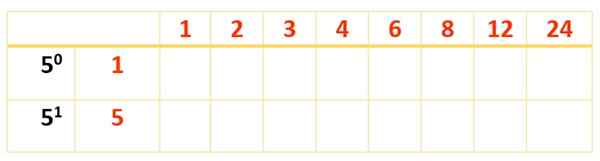
Nå er tabellen fullført med produktene fra tallene i rødt, som det ble gjort med den første tabellen:

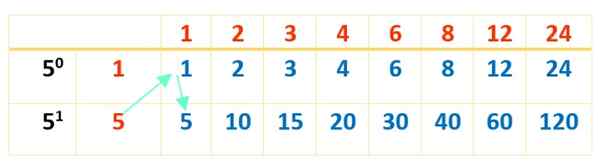
Og til slutt vises de 16 delene av 120 i blått. Bordene er en utmerket hjelp for operasjoner som skal gjøres i orden og dermed nr. 120 divisor.

Løste øvelser

Prosedyren for å finne alle delere av et tall er oppsummert som følger:

1. Bryt ned antallet i primfaktorer.
2. Beregn antall delinger med formelen.
3. Bygg de nødvendige tabellene for å finne deling. Hvis tallet har to faktorer, er en tabell nok, hvis du har tre faktorer, må to tabeller lages, som i tilfelle av 120.

Oppgave 1

Finn alle delingene av 288.

Løsning

288 dekomponerer til primære faktorer:

288 | 2
144 | 2
72 | 2
36 | 2
18 | 2
9 | 3
3 | 3
1 | 1

288 er skrevet slik:

288 = 2⁵ ∙ 3²

Umiddelbart er antallet deling av 288 til:

Antall divisorer = (n +1) × (m +1) × (p +1) ... × (k +1)

Fra nedbrytningen i primære faktorer bemerkes det at n = 5 og m = 2, da:

Divisorer på 288 = (5 +1) × (2 +1) = 6 × 3 = 18

Det er 18 divisorer, og siden det bare er to faktorer, er det tilstrekkelig med bare ett tabell:

Kan tjene deg: Kjennetegn på rektangelet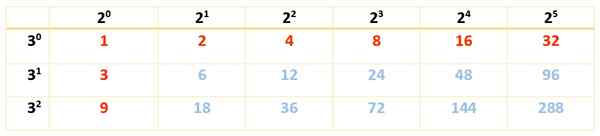

Divisorene på 288 er tallene i rødt og i blått:

Div (288) = 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144, 288

De kan sjekkes raskt ved hjelp av en kalkulator.

Oppgave 2

Finn delingene av 350

Løsning

350 dekomponerer:

350 | 2
175 | 5
35 | 5
7 | 7
1 | 1

350 kan skrives som et produkt av tre faktorer:

350 = 2 ∙ 5²∙ 7

Neste trinn er å beregne hvor mange delere som har, gjennom formelen:

Antall divisorer = (n +1) × (m +1) × (p +1) ... × (k +1)

Med n = 1, m = 2, p = 1

Divisorer på 288 = (1 +1) × (2 +1) × (1 +1) = 2 × 3 × 2 = 12

Ettersom 350 krever tre faktorer, må to tabeller lages. Den første er ferdig med 2 og 5², Men det kan også gjøres med 2 og 7, eller med 7 og 5², I henhold til preferansen, siden i alle former, er det endelige resultatet det samme:

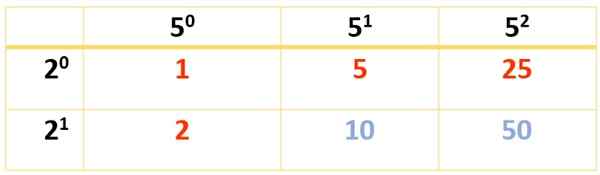
6 Divisors oppnås. De andre vises ved hjelp av denne andre tabellen:

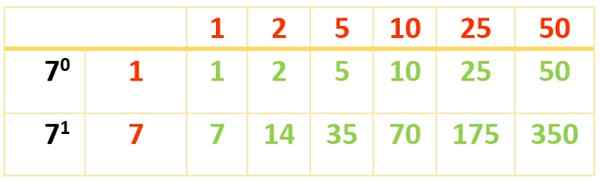
Divisorene på 350 er:

Div (350) = 1, 2, 5, 7, 10, 14, 25, 35, 50, 70, 175, 350