Kontinuitetsligning

Vi forklarer hva som er kontinuitetsligningen, dens formel, applikasjoner, eksempler og foreslår øvelser for å løse

Hva er kontinuitetsligningen?

De Kontinuitetsligning, For inkomprimerbar væske fastslår den at den totale massen til en væske som sirkulerer gjennom et rør, uten tap eller fortjeneste, forblir konstant. Med andre ord, deigen er bevart uten endringer når væsken beveger seg.

En inkomprimerbar væske er at hvis tetthet forblir omtrent konstant mens du flyter. For eksempel er vann en væske som anses som inkomprimerbar under standard trykk- og temperaturforhold.

Det er en matematisk måte å uttrykke bevaring av masse, i kontinuitetsligningen, gitt av:

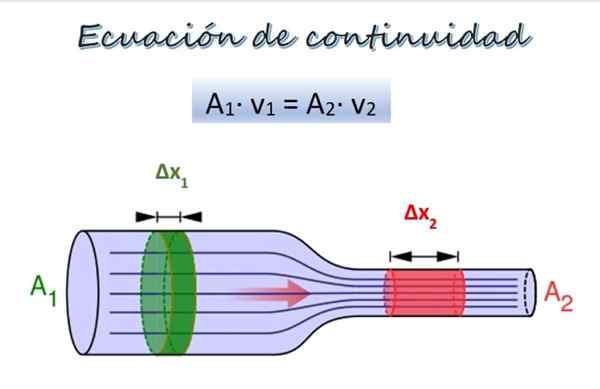
TIL₁∙ V₁ = A₂∙ V₂

Hvor v₁ og v₂ De representerer hastigheten på væsken i to seksjoner av et rør, mens₁ allerede₂ De er de respektive krysset -avsetningsområdene.

Produktet av kors -spekterområdet etter hastighet kalles strømme Og kontinuitetsligningen innebærer at strømmen gjennom røret er konstant. Strømmen er også kjent som Volumstrømningshastighet, Det forstås ved å nøye observere det forrige uttrykket, hvis dimensjoner er volum per tidsenhet.

Formel

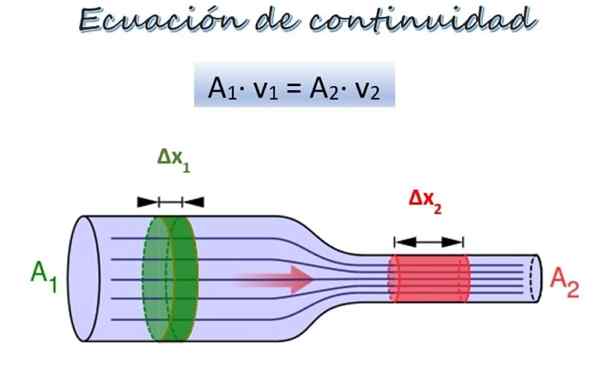Kontinuitetsligningen for strømmen av en væske langs et rør med forskjellige diametre. Kilde: Wikimedia Commons/F. Zapata.

I det øvre bildet er det et rør med to seksjoner med forskjellig diameter og i samme høyde, selv om de kan være i forskjellige høyder uten å representere et problem.

I avsnitt 1, bredere, er det kryssende spisseksjonsområdet til₁ og væsken beveger seg med hastighet v₁, Mens du er i seksjon 2, smalere, er krysset₂ og hastigheten på væsken er v₂.

En deigdel Δm₁ (grønn) beveger seg etter seksjon 1 i en tid Δt. I løpet av denne perioden, delen Δm₂ (rød) reise gjennom seksjon 2. Ettersom væsken er inkomprimerbar, er tettheten den samme i alle punktene, så fra definisjonen av tetthet:

Det kan tjene deg: Gasekonstant: Hva er, beregning og eksempler

Her ρ er tetthet, M er massen og V -volumet. I følge dette er massen ΔM₁ er lik:

Δm₁ = ρ ∙ V₁

Hvor volum v₁ Det er produktet mellom tverrsnittet og avstanden Δx₁:

Δm₁ = ρ ∙ (a₁ ∙ Δx₁)

Men siden:

Deretter deigdelen Δm₁ Du kan skrive, når det gjelder hastighet og tid ΔT som:

Δm₁ = ρ ∙ a₁ ∙ Δx₁ = ρ ∙ a₁ ∙ (v₁ ∙ Δt)

Analog delen Δm er skrevet₂ Det flyter samtidig med avsnitt 2:

Δm₂ = ρ ∙ a₂ ∙ Δx₂ = ρ ∙ a₂ ∙ (v₂ ∙ Δt)

Ved bevaring av massen:

Δm₁ = Δm₂

OG:

ρ ∙ a₁ ∙ V₁ ∙ Δt = ρ ∙ a₂ ∙ V₂ ∙ Δt

Som Δt og ρ blir kansellert, resultater:

TIL₁ ∙ V₁ = A₂ ∙ V₂

Strømmen q

Produktet av tverrsnittet A med hastigheten på væsken V kalles flyt og betegner som q. Det tilsvarer væskevolumet per tidsenhet gjennom røret, eller volumstrømningshastigheten:

 V Volum og ΔT tidsintervallet. Strømningshastigheten i det internasjonale systemet med enheter er m³/s, selv om kubikkføtter, gallon/min, gallons/s a liter/s og gallons/s er hyppige. Noen av de mest brukte konverteringsfaktorene er følgende:

• 1 m³/S = 264.172 gal/s
• 1 l/s = 0.001 m³/s
• 1 ft³/S = 0.0283168 m³/s
• 1 l/s = 0,264172 gal/s
• 1 m³/S = 15850,3 gal/min

Legg merke til at ved å redusere tverrsnittet av røret øker væskens hastighet, og omvendt, hvis tverrsnittet øker, reduseres hastigheten slik at strømmen er konstant.

Applikasjoner og eksempler

Kontinuitetsligningen brukes i analysen av væskestrømmen, i kombinasjon med Bernoulli -ligningen, der variasjonene av hastigheten på væsken i de forskjellige seksjonene tas i betraktning, samt trykkendringene og effekten av høyden.

Kan tjene deg: Diktstrøm

Eksempel 1

I familiens hageslange, når vannet normalt forlater jet har et visst område, men hvis den setter fingeren ved utgangen av slangen, og reduserer utgangshullet, er jetområdet større.

Her er kontinuitetsligningen oppfylt, sidenstreken, ved å redusere arealet til utgangsdysen, øker hastigheten på strålen slik at hastighetsområdet etter hastighet er konstant.

Eksempel 2

Vannstrålen smalner når den faller, siden hastigheten øker. På denne måten forblir produkthastigheten per område konstant

Et annet eksempel der kontinuitetsligningen blir fremhevet er vannstrålen som smalner når den faller, på grunn av økningen i vannhastigheten i løpet av høsten.

På denne måten er strømmen konstant, mens jet fortsetter å strømme i et laminært regime, det vil si at vannet faller forsiktig uten turbulens eller virvler.

Løste øvelser

Oppgave 1

Vann sirkulerer gjennom et rør på 20 cm diameter. Å vite at strømmen er 2000 l/s, finn vannets hastighet i røret.

• Løsning

Det er praktisk å uttrykke alt i enheter av det internasjonale systemet. For det første beregnes krysseseksjonsseksjonen av røret, og husker at radius er halvparten av diameteren:

A = π ∙ (d/2)²

D = 20 cm = 0.2 m

Derfor er området:

A = π ∙ (d/2)² = A = π ∙ (0.2 m /2)² = 0.0314 m².

Strømmen er uttrykt i m³/s ved hjelp av passende konverteringsfaktor:

Q = 2000 l/s = 2 m³/s

Fra formelen q = a ∙ V hastigheten som væsken sirkulerer gjennom røret er fjernet:

Oppgave 2

Du har et variabelt kryss -avsnittsrør som vannet strømmer. På et bestemt tidspunkt er tverrsnittet 0.070 m² Og vannets hastighet er 3.50 m/s. Regne ut:

Kan tjene deg: Pascal prinsipp: Historie, applikasjoner, eksempler

a) vannhastigheten på et annet punkt i røret hvis tverrsnittsareal er 0.105 m².

b) Volumet av vann som slippes ut av en åpen ende på 1 time.

• Løsning på

Kontinuitetsligningen brukes, og samsvarer med strømmen av det første punktet med strømmen av det andre. Strømmen er:

Q = a ∙ V

For kontinuitet:

Q₁ = Q₂

TIL₁ ∙ V₁ = A₂ ∙ V₂

Nå erstatter de dataene levert av uttalelsen:

• TIL₁ = 0.070 m²
• v₁ = 3.50 m/s
• TIL₂ = 0.105 m²
• v₂ =?

Og Clears v₂:

Løsning b

Siden strømmen også er volumet per tidsenhet, må den:

Derfor er bind V:

V = q ∙ Δt = (a ∙ v) Δt

Flyten som kan beregnes med dataene fra punkt 1 eller for punkt 2, siden den er den samme på begge punktene:

Q = a₁ ∙ V₁ = 0.070 m² ∙ 3.50 m/s = 0.245 m³ / s

Når vi vet at 1 time = 3600 s, er volumet av vann som slippes ut:

V = q ∙ Δt = (0.245 m³ / s) × (3600 s) = 882 m³

Om 1 time 882 m lastes ned³ vann gjennom røret.