Generell ligning av en linje hvis skråning er lik 2/3

Den generelle ligningen på en linje l er som følger: AX+av+c = 0, der a, b og c er konstant, x er den uavhengige variabelen e og den avhengige variabelen.

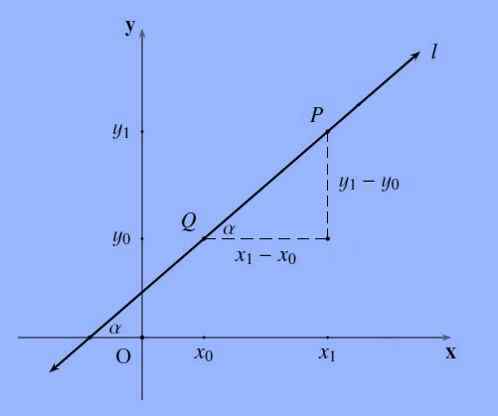
Hellingen til en linje, betegnet på en generell måte med bokstav M, som går gjennom punktene P = (x1, y1) og q = (x0, y0) er følgende kvotient m: = (y1-y0)/(x1 -X0).

Hellingen til en rett linje representerer tilbøyeligheten; Sagt mer formelt er skråningen på en linje tangenten i vinkelen som denne formen med x -aksen.

Det skal bemerkes at rekkefølgen som punktene er navngitt er likegyldig, siden (Y0-Y1)/(x0-x1) =-(Y1-y0)/(-(x1-x0)) = (Y1-y0) /(X1-x0).

I påvente av linjen

Hvis det er kjent to punkter som en linje passerer, er det enkelt å beregne skråningen. Men hva som skjer hvis disse punktene ikke er kjent?

Gitt den generelle ligningen til en øks+med+c = 0 linje, må den.

Hva er den generelle ligningen på en linje hvis skråning er 2/3?

Ettersom linjens skråning er 2/3, er likestilling etablert -A/B = 2/3, som kan se at A = -2 og B = 3. Slik at den generelle ligningen for en linje med skråningen lik 2/3 er -2x+3y+C = 0.

Det skal avklares at hvis du er valgt a = 2 og b = -3, vil den samme ligningen oppnås. Faktisk 2x -3y+c = 0, som er lik den forrige multipliseres med -1. Tegnet på C spiller ingen rolle, siden det er en generell konstant.

En annen observasjon som kan gjøres er at for A = -4 og B = 6 oppnås den samme linjen, selv om dens generelle ligning er forskjellig. I dette tilfellet er den generelle ligningen -4x+6y+c = 0.

Er det andre måter å finne den generelle ligningen på linjen?

Svaret er ja. Hvis skråningen på en linje er kjent, er det to former, ekstra til den forrige, for å finne den generelle ligningen.

For dette brukes den punktsøkende ligningen og skjæreligningen.

-Den punktsøkende ligningen: Hvis m er skråningen til en linje og p = (x0, y0) et punkt der den passerer, kalles ligningen.

-Den skjærende avhengende ligningen: Hvis m er skråningen til en linje og (0, b) er kuttet på linjen med y-aksen, kalles ligningen.

Ved bruk av det første tilfellet oppnås det at den punkt-anvendte ligningen av en linje hvis skråning er 2/3 er gitt av uttrykket y-y0 = (2/3) (X-x0).

For å nå den generelle ligningen, multipliseres alle begrepene med 3 på begge sider og er gruppert sammen, og oppnår dermed at -2x+3y+(2 × 0-3y0) = 0 er den generelle ligningen på linjen, der c = 2 × 0-3y0.

Hvis det andre tilfellet brukes, oppnås det at den skjærende avhengige ligningen på en linje hvis skråning er 2/3 er y = (2/3) x+b.

Igjen, multipliserer 3 på begge sider, og grupperer alle variablene, oppnås den -2x+3y -3b = 0. Sistnevnte er den generelle ligningen på linjen der C = -3b.

Når man ser nøye på begge tilfeller, kan det sees at det andre tilfellet ganske enkelt er et spesielt tilfelle av den første (når x0 = 0).