Førsteklasses ligningsformel, hvordan du løser dem, eksempel, øvelser

De Første grad eller lineære ligninger Med en ukjent er de som kan uttrykkes som summen av to vilkår, på følgende måte:

AX + B = 0

Hvor a og b, med til ≠ 0, er reelle tall r eller også komplekser c. For å løse det blir vilkår transponert, noe som betyr å endre begreper fra en side til en annen av likhet.

Figur 1. En lineær ligning er y = mx + c form med y = 0. Kilde: Pxhere.

For å fjerne det ukjente, blir begrepet +B transponert, som må gå til høyre side av likhet med et endret tegn.

AX = -B

Da blir verdien av x fjernet, på denne måten:

x = - b/a

Som et eksempel vil vi løse følgende ligning:

6x - 5 = 4

Vi transponerer begrepet -5 til høyre side med et endret tegn:

6x = 4 + 5

Dette tilsvarer å legge til 5 på begge sider av den opprinnelige ligningen:

6x - 5 + 5 = 4 + 5 → 6x = 9

Og nå fjerner vi det ukjente "X":

x = 9/6 = 3/2

Som tilsvarer å dele begge sider av likhet med 6. Så vi kan vurdere følgende for å oppnå løsningen:

-Den samme mengden kan legges til eller trukket fra begge sider av likhet i en ligning, uten å endre den.

-Du kan også multiplisere (eller dele) med samme mengde til alle vilkår både til venstre og til høyre for ligningen.

-Og hvis begge medlemmene av en ligning stiger til samme makt, endres ikke likheten heller.

[TOC]

Hvordan du løser første grads ligninger

Løsningen av en første grads ligning er også kjent som roten til den samme. Det er verdien av x som konverterer det opprinnelige uttrykket til en likhet. For eksempel i:

5x = 8x - 15

Hvis vi erstatter x = 5 i denne ligningen, oppnås det:

5⋅5 = 8⋅5 - 15

25 = 40 - 15

25 = 25

Ettersom den første graden lineære ligninger kommer på mange måter, som noen ganger ikke er tydelige, er det en serie generelle regler som omfatter flere algebraiske manipulasjoner, for å finne verdien av det ukjente:

-For det første, hvis det er angitt operasjoner, må disse utføres.

-Grupperingssymboler som parentes, firkantede parenteser og nøkler, hvis de eksisterer, må undertrykkes ved å opprettholde de aktuelle tegnene.

-Begrepene overføres for å plassere alle de som inneholder det ukjente for en enkelt side av likhet, og de som ikke inneholder det til den andre.

-Da reduseres alle lignende vilkår for å nå skjemaet AX = -B.

-Og det siste trinnet er å fjerne det ukjente.

Grafisk tolkning

Den første gradslikningen hevet i begynnelsen kan avledes fra ligningen på linjen y = mx+c, og gjør y = 0. Verdien av x som resulterer tilsvarer skjæringspunktet mellom linjen med den horisontale aksen.

I den følgende figuren har du tre linjer. Starter med den grønne linjen, hvis ligning er:

Kan tjene deg: faktorisering

y = 2x - 6

Å lage y = 0 i linjen for linjen Førstgradsligningen oppnås:

2x - 6 = 0

Hvis løsning er x = 6/2 = 3. Nå når vi detaljerer grafen, er det lett å innse at linjen faktisk kutter til den horisontale aksen ved x = 3.

Den blå linjen krysser x -aksen ved x = 5, som er løsningen på ligningen -X + 5 = 0. Endelig linjen hvis ligning er y = 0.5x + 2 kuttet til x -aksen ved x = -4, som lett blir advart om første grads ligning:

0.5 x + 2 = 0

x = 2/0.5 = 4

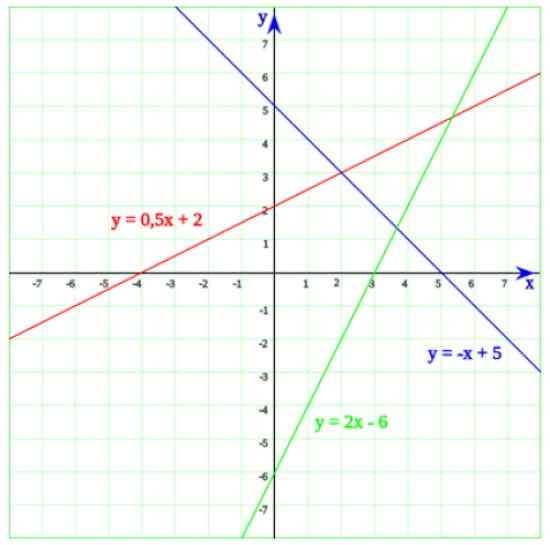Figur 2. Tre linjer hvis kryss med den horisontale aksen tilsvarer lineære ligninger. Kilde: Wikimedia Commons.

Eksempler på enkle lineære ligninger   

Hele ligninger

De er de som for eksempel ikke er noen nevner, for eksempel:

21 - 6x = 27 - 8x

Løsningen er:

-6x + 8x = 27 - 21

2x = 6

x = 3

Fraksjonelle ligninger

Disse ligningene inneholder minst en annen nevner av 1. For å løse dem, anbefales det.

Følgende ligning er brøktype:

Nevnerne er 6, 8 og 12 og deres minimum vanlige multiplum, betegnet som m.c.M (6, 8,12) er den minste av tallene som inneholder disse nevnerne.

Siden disse tallene er små, er det ikke vanskelig å se at m.c.M (6, 8,12) = 24. Dette resultatet oppnås enkelt ved å uttrykke tall som et produkt av primtall eller deres krefter, la oss se:

6 = 3.2

8 = 2³

12 = 2²⋅3

Minste vanlige multiplum bestemmes ved å multiplisere de vanlige og ikke -vanlige faktorene på 6, 8 og 12 med sin største eksponent, deretter:

MCM (6,8,12) = 2³ ⋅3 = 8 × 3 = 24

Siden minimumsmultippelen er tilgjengelig, må det multipliseres med hvert av vilkårene i ligningen:

På denne måten blir nevnerne undertrykt og det er en ligning med produkter, lettere å løse:

4 (x+5) -3 (2x+3) = 2 (1-5x)

Vi benytter oss av distribusjonseiendommer:

4x + 20 - 6x -9 = 2 - 10x

Alle vilkårene som inneholder det ukjente "X" er gruppert til venstre side av likhet, og etterlater de uavhengige eller numeriske vilkårene på høyre side:

4x - 6x + 10 x = 2 +9 - 20

8x = -9

x = - 9/8

Bokstavelige ligninger

De er lineære ligninger med en ukjent, som imidlertid er ledsaget av bokstavelige koeffisienter (bokstaver). Disse bokstavene blir behandlet akkurat som det ville bli gjort med tallene. Et eksempel på en bokstavelig førstegradsligning er:

-3ax + 2a = 5x - b

Denne ligningen løses på samme måte som om de uavhengige begrepene og koeffisientene var numeriske:

-3ax - 5x = - b - 2a

Factoring av det ukjente "X":

x (-3a - 5) = - b - 2a

x = ( - b - 2a) / (-3a - 5) → x = (2a + b) / (3a + 5)

Første grad ligningssystemer 

Ligningssystemer består av et sett med ligninger med to eller flere ukjente. Systemløsningen består av verdier som tilfredsstiller ligninger samtidig og for å bestemme den utvetydig, må det være en ligning for hver ukjente.

Kan tjene deg: vektor algebra

Den generelle formen for et system av m Lineære ligninger med n Ukjente er:

til_ellevex₁ + til₁₂x₂ +… til_1nx_n = b₁
til_tjueenx₁ + til₂₂x₂ +… til_2nx_n = b₂
..
til_M1x₁ + til_M2x₂ +… til_mnx_n = b_m

Hvis systemet har en løsning, sies det at det er det bestemt kompatibel, Når det er et uendelig sett med verdier som tilfredsstiller det, er det ubestemt kompatibel, Og til slutt, hvis det ikke har noen løsning, er det det uforenlig.

I oppløsningen av lineære ligningssystemer brukes flere metoder: reduksjon, erstatning, utjevning, grafiske metoder, Gauss-Jordan eliminering og bruk av determinanter er blant de mest brukte. Men det er andre algoritmer for å nå løsningen, mer praktisk for systemer med mange ligninger og ukjente.

Et eksempel på et system med lineære ligninger med to ukjente er:

8x - 5 = 7y - 9
6x = 3y + 6

Løsningen av dette systemet sendes inn senere i delen Løste øvelser.

Lineære ligninger med absolutt verdi

Den absolutte verdien av et reelt tall er avstanden mellom plasseringen på tallinjen og 0 av den samme. Å være en avstand verdien er alltid positiv.

Den absolutte verdien av et tall er betegnet med modulstenger: │x│. Den absolutte verdien av et positivt eller negativt tall er alltid positiv, for eksempel:

│+8│ = 8

│-3│ = 3

I en ligning med absolutt verdi er det ukjente mellom modulstenger. Tenk på følgende enkle ligning:

│x│ = 10

Det er to muligheter, den første er at X er et positivt tall, i hvilket tilfelle vi har:

x = 10

Og den andre muligheten er at X er et negativt tall, i dette tilfellet:

x = -10

Dette er løsningene på denne ligningen. La oss nå se et annet eksempel:

│x+6│ = 11

Mengden i stolpene kan være positivt, da:

x+6 = 11

x = 11 -6 = 5

Eller kan være negativ. I så fall:

-(x+6) = 11

-x - 6 = 11 ⇒ -x = 11+6 = 17

Og verdien av det ukjente er:

x = -17

Denne absolutte verdi -ligningen har derfor to løsninger: x₁ = 5 og x₂ = -17. Vi kan bekrefte at begge løsningene fører til likhet i den opprinnelige ligningen:

│5+6│ = 11

│11│ = 11

OG

│-17+6│ = 11

│-11│ = 11

Enkle løste øvelser

- Oppgave 1

Løs følgende system med lineære ligninger med to ukjente:

8x - 5 = 7y -9
6x = 3y + 6

Løsning

Når dette systemet er hevet, er det egnet for å bruke erstatningsmetoden, siden i den andre ligningen den ukjente x Det er nesten klar for klarering:

x = (3y + 6)/6

Kan tjene deg: algebraic

Og du kan umiddelbart erstatte den første ligningen, som deretter blir en første -gradering ligning med ukjent "y":

8 [(3y + 6)/6] - 5 = 7y - 9

Denominatoren kan undertrykkes hvis hvert begrep multipliseres med 6:

6 . 8⋅ [(3y + 6)/6] - 6.5 = 6 .7y- 6 . 9

8⋅ (3y + 6) - 30 = 42y - 54

Bruke distribusjonseiendommer i første periode til rettighetsretten:

24y + 48 -30 = 42y - 54 ⇒ 24y + 18 = 42y - 54

Ligningen kan forenkles, siden alle koeffisienter er multipler av 6:

4y + 3 = 7y - 9

-3y = -12

y = 4

Med dette resultatet går vi til klarering av x:

x = (3y +6)/6 → x = (12 +6)/6 = 3

- Oppgave 2

Løs følgende ligning:

Løsning

I denne ligningen vises produkter, og etter instruksjonene som er gitt i begynnelsen, må de først utvikles:

3x - 10x +14 = 5x + 36x + 12

Da blir alle vilkårene som inneholder de ukjente ført til venstre side av likhet, og på høyre side vil de uavhengige begrepene være:

3x - 10x - 5x - 36x = 12 - 14

-48x = -2

x = 1/24

- Øvelse 3

Ved å legge de tre indre vinklene til en trekant, oppnås 180º. Den største overstiger barnet i 35º, og dette overstiger igjen i 20 º forskjellen mellom den største og medium. Hva er vinklene?

Løsning

Vi vil kalle "x" til hovedvinkelen, "y" til mediet og "z" til barnet. Når uttalelsen sier at summen av dem er 180º, kan du skrive:

x + y + z = 180

Da vet vi at den eldste overstiger barnet i 35º, vi kan skrive dette:

X = z + 35

Til slutt overstiger barnet i 20 º til forskjellen mellom det største og medium:

Z = x - y + 20

Vi har et system med 3 ligninger og 3 ukjente:

x + y + z = 180

X = z + 35

Z = x - y + 20

Ved å rydde den første ligningen har du:

Z = 180 - x - y

Matcher den tredje:

180 - x - y = x - y + 20

Å gi de ukjente til venstre som alltid:

-x - y - x + y = 20 - 180

"Y" blir kansellert og gjenstår:

-2x = - 160

x = 80º

Den andre ligningen er verdien av z:

Z = x - 35 = 80 - 35 = 45º

Og verdien av og er av den første eller tredje:

y = 180 - x - z = 180 - 80 - 45 = 55º

Referanser

1. Baldor. 1977. Elementær algebra. Venezuelanske kulturutgaver.
2. Monterey Institute. Ligninger, ulikheter og absolutt verdi. Gjenopprettet fra: MontereyInstitute.org.
3. Online lærer. Klassifisering av lineære eller førstegrads ligninger. Gjenopprettet seg fra: Professor Inline.Cl.
4. Hoffman, J. Valg av matematikkproblemer. Volum 2.
5. Jiménez, r. 2008. Algebra. Prentice Hall.
6. Zill, d. 1984. Algebra og trigonometri. McGraw Hill.