Andre grads ligningsformel, hvordan du løser dem, eksempler, øvelser
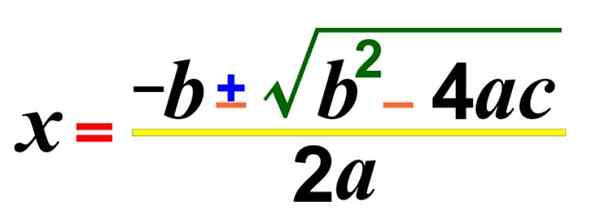
- 4797
- 1461
- Magnus Sander Berntsen
De Andre grad eller kvadratiske ligninger Og en ukjent har skjemaet øks2 + BX + C = 0. Der A ≠ 0, siden det var 0, ville ligningen bli transformert til en lineær ligning, og koeffisienter A, B og C er reelle tall.
Det ukjente som skal bestemmes er verdien av x. For eksempel 3x -ligningen2 - 5x + 2 = 0 er en komplett andre grads ligning.
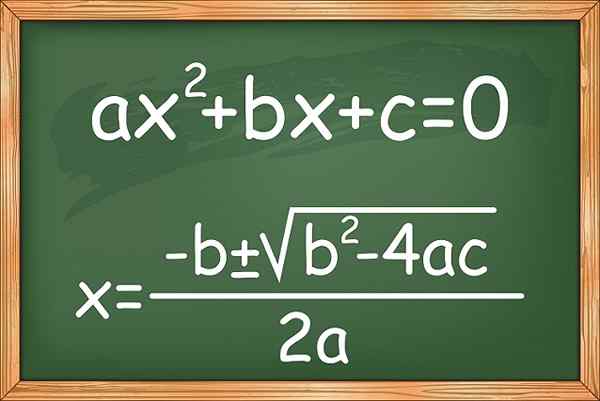 Figur 1. Formelen for å løse andre grad eller kvadratiske ligninger av en ukjent
Figur 1. Formelen for å løse andre grad eller kvadratiske ligninger av en ukjent Det er også varianter som er kjent som ufullstendige sekundegradsligninger, som mangler noen av vilkårene, bortsett fra det av øks2. Her er noen eksempler:
x2 - 25 = 0
3x2 - 5x = 0
Al Juarismi, den berømte arabiske matematikeren av antikken, beskrevet i sine verk forskjellige typer første og andre grads ligninger, men bare med positive koeffisienter. Imidlertid var det den franske matematiske Oppløsning:
Dette er en generell formel som gjør det mulig. Det er også andre måter å løse dem på.
[TOC]
Hvordan løse ligninger i andre klasse?
Andre -grads ligninger kan løses med formelen gitt ovenfor, og det er også andre algebraiske prosedyrer som kan fungere i noen ligninger.
Vi kommer til å løse den foreslåtte ligningen i begynnelsen med formelen, en gyldig metode for en hvilken som helst annen grads ligning med en ukjente:
3x2 - 5x + 2 = 0
For å bruke formelen bemerker vi riktig at:
- til Det er koeffisienten for begrepet med x2
- b Det er koeffisienten for det lineære begrepet
- c er det uavhengige begrepet.
La oss identifisere dem fra samme ligning:
A = 3
B = -5
C = 2
Merk at tegnet som følger med koeffisienten, må tas i betraktning. Nå erstatter vi disse verdiene i formelen:
I telleren er symbolet på "mer - mindre" ±, noe som indikerer at mengden med rot kan tas som positiv og også som negativ. En andre grads ligning har maksimalt to virkelige løsninger, og dette symbolet tar det i betraktning.
La oss ringe x1 og x2 Til disse to løsningene, da:
x1 = (5+1) / 6 = 1
x2 = (5-1)/6 = 4/6 = 2/3
Oppløsning ved faktorisering
Noen andre grads ligninger består av trinomialer som er lett faktor. I så fall er denne metoden mye raskere. Tenk på ligningen:
x2 + 7x - 18 = 0
Faktorisering har dette skjemaet:
Kan tjene deg: kongruens: kongruente figurer, kriterier, eksempler, øvelser(x +) ⋅ (x -)
De blanke mellomrommene er fylt med to tall som, når de multipliseres i 18, og når de blir trukket fra, er 7 7. Skiltene i parenteser er valgt med dette kriteriet:
-I den første parentesen er tegnet mellom den første og den andre termen plassert.
-Og i den andre parentesen går produktet av skiltene som blir sett.
Når det gjelder tallene, er de lett i dette tilfellet: de er 9 og 2. Den eldste er alltid plassert i den første av parentesen, som dette:
x2 + 7x - 18 = (x + 9). (x - 2)
Leseren kan sjekke gjennom distribusjonseiendom, som når man utvikler produktet av høyre side av likhet, oppnås trinomial til venstre. Nå blir ligningen omskrevet:
(x + 9) ⋅ (x - 2) = 0
For at likestilling skal oppfylles, er det nok for en av de to faktorene å være null. Så i den første må det gjøres1 = -9 eller det kan være at den andre faktoren blir kansellert, i så fall x2 = 2. Dette er ligningsløsningene.
Grafisk metode
Røttene eller løsningene av andre grads ligning tilsvarer skjæringspunktene i lignelsen y = = = øks2 + bx + c Med den horisontale aksen eller x -aksen. Slik at ved å tegne den tilsvarende lignelsen, finner vi løsningen av andre grads ligning som gjør y = 0.
Kuttene til lignelsene med den horisontale aksen representerer ligningens løsningene øks2 + BX + C = 0. En lignelse som bare kutter den horisontale aksen på et enkelt punkt har en enkelt rot, og dette vil alltid være toppunktet til parabolen.
Og til slutt, hvis en lignelse ikke kutter seg til den horisontale aksen, den tilsvarende ligningen øks2 + BX + C = 0 Det mangler reelle løsninger.
Å bygge en håndgraf kan være arbeidskrevende, men med bruk av programmer som graf online er det veldig enkelt.
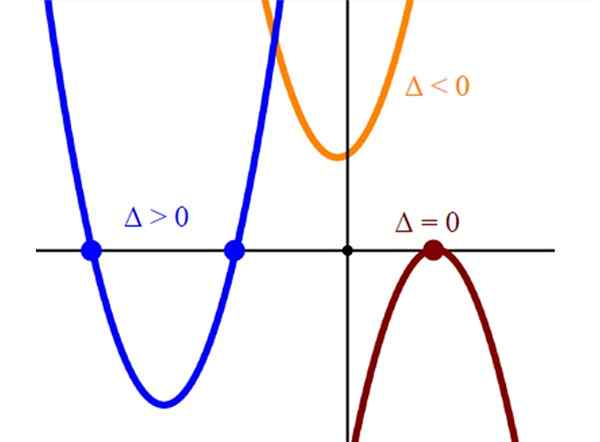 Figur 2. Grafisk representasjon av tre typer lignelser, med to, ett og ingen kryss med den horisontale aksen. Kilde: Wikimedia Commons.
Figur 2. Grafisk representasjon av tre typer lignelser, med to, ett og ingen kryss med den horisontale aksen. Kilde: Wikimedia Commons. Oppløsning med vitenskapelig kalkulator
Mange modeller av vitenskapelige kalkulatorer har muligheten til å løse andre grads ligninger (og også andre typer ligninger). For å vite det, må du gå gjennom menyen.
Når det kvadratiske ligningsalternativet til en ukjent er valgt, ber menyen om å legge inn verdiene til koeffisientene A, B og C og returnere de virkelige løsningene hvis de eksisterer. Og det er også modeller av vitenskapelige kalkulatorer som jobber med komplekse tall og tilbyr disse løsningene.
Kan tjene deg: Multipler av 2: Hva er og forklaringDiskriminere fra en andre grads ligning
For å vite om ligningen har reelle løsninger eller ikke, og hvor mange, uten behov for å løse først, er diskriminerende definert som mengden under kvadratroten:
Δ = b2 - 4ac
I henhold til diskriminerende tegnet er det kjent hvor mange løsninger ligningen har i henhold til dette kriteriet:
-To virkelige løsninger: Δ> 0
-En ekte løsning (eller to identiske løsninger): Δ = 0
-Ingen reell løsning: Δ < 0
For eksempel hvor mange løsninger har andre grads ligning -7x2 +12x + 64 = 0? Vi identifiserer koeffisientene:
A = -7
B = 12
C = 64
Δ = b2 - 4ac = 122 - 4x (-7) x 64 = 144 + 1792 = 1936> 0
Ligningen har to løsninger. La oss nå se denne:
x2 - 6x + 9 = 0
A = 1
B = -6
C = 9
Δ = (-6)2 - 4 x 1 x 9 = 36 - 36 = 0
Dette er en ligning med en unik løsning eller to like løsninger.
Eksempler på enkle andre grads ligninger
I begynnelsen sa vi at andre grads ligninger kan være komplette hvis trinomialen er, og ufullstendig hvis det lineære begrepet eller det uavhengige uttrykket manglet. La oss nå se noen spesielle typer:
X Form ligning2 + mx + n = 0
I dette tilfellet A = 1 og formelen reduseres til:
For denne typen ligninger, og alltid avhengig av de gjenværende koeffisientene, kan faktoriseringsmetoden fungere bra, som vi så i foregående avsnitt.
Ufullstendig ligning av øksformen2 + C = 0
Løsningen, hvis den eksisterer, er formen:
Det er reell løsning når en O C har et negativt tegn, men hvis de to begrepene har samme tegn, vil løsningen være tenkt.
Ufullstendig ligning av øksformen2 + BX = 0
Denne ligningen løses raskt ved å bruke faktorisering, siden X er en vanlig faktor i begge termer. En av løsningene er alltid x = 0, den andre er slik:
øks2 + BX = 0
x (øks + b) = 0
øks + b = 0 → x = -b/a
La oss se på et eksempel da. Løse:
x2 - 5x = 0
x (x - 5) = 0
Derfor x1 = 0 og x2 = 5
Ligninger med nevner
Det er flere rasjonelle ligninger, der det ukjente kan være til stede både i telleren og i nevneren, eller til og med bare i sistnevnte, og at ved algebraiske manipulasjoner reduseres til kvadratiske ligninger.
Måten å løse dem på er å multiplisere begge sider av likhet med minimum av felles multiplum eller m.c.m av nevnerne og omorganiserer vilkårene. For eksempel:
Kan tjene deg: hvor mange diametre har en omkrets?Høyere ordensligninger som blir omgjort til kvadratisk
Det er høyere ordensligninger som gjennom en variabel endring kan løses som om de var kvadratiske, for eksempel denne ligningen Bicadrada:
x4 - 10x2 + 9 = 0
La x2 = U, så blir ligningen omgjort til:
eller2 - 10U + 9 = 0
Denne ligningen løses raskt ved faktorisering, og finner to tall som multipliseres i 9 og tilsatt 10. Disse tallene er 9 og 1:
(U - 9).(U - 1) = 0
Derfor er løsningene på denne ligningen u1 = 9 og u2 = 1. Nå returnerer vi endringen:
x2 = 9 → x1 = 3 og x2 = -3
x2 = 1 → x1 = 1 og x2 = -1
Den opprinnelige ligningen er av orden 4, derfor har den minst 4 røtter. Eksemplet er -3, -1, 1 og 3.
Enkle løste øvelser
- Oppgave 1
Løs følgende kvadratiske ligning med det ukjente i nevneren:
Minimum vanlig multiplum er x (x+2) og må multiplisere til alle vilkår:
Det tilsvarende uttrykket gjenstår:
5x (x+2) - x = x (x+2)
Vi utvikler:
5x2 + 10x - x = x2 + 2x
Alle vilkår overføres til venstre for likhet og til høyre er venstre 0:
5x2 + 10x - x - x2 - 2x = 0
4x2 - 7x = 0
Vi faktor, siden det er en ufullstendig ligning:
x (4x - 7) = 0
En av løsningene er x = 0, den andre er:
4x = 7
x = 7/4
- Oppgave 2
Finn løsningen av andre grads ligninger:
a) -7x2 +12x + 64 = 0
b) x2 - 6x + 9 = 0
Løsning på
Fra denne ligningen kjenner vi Δ determinanten, fordi den ble beregnet som et eksempel før, så vi kommer til å dra nytte av den, og uttrykke løsningsmiddelformelen som følger:
x1 = (-12+44)/ - 14 = - (32/14) = - (16/7)
x2 = (-12 -44) / -14 = 4
Løsning b
Den firkantede trinomial x2 - 6x + 9 er faktoriserbar, siden det er en perfekt firkantet trinomial:
x2 - 6x + 9 = (x-3)2 = 0
Løsningen av denne ligningen er x = 3.
- Øvelse 3
Hva er ligningen hvis løsninger er 3 og 4?
Løsning
Det faktoriserte uttrykket er:
(x - 3) ⋅ (x - 4) = 0
Bruke distribusjonseiendom:
x2 - 4x -3x + 12 = 0
De to sentrale begrepene er like og kan reduseres, og være: å forlate:
x2 - 7x + 12 = 0
Referanser
- Baldor. 1977. Elementær algebra. Venezuelanske kulturutgaver.
- Hoffman, J. Valg av matematikkproblemer. Volum 2.
- Jiménez, r. 2008. Algebra. Prentice Hall.
- Stewart, J. 2006. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
- Zapata, f. 4 måter å løse en andre grads ligning på. Gjenopprettet fra: Francesphysics.Blogspot.com.
- Zill, d. 1984. Algebra og trigonometri. McGraw Hill.
- « Tilleggspolymerstruktur, egenskaper, funksjon, bruk
- Intrinsiske motivasjonskarakteristikker og eksempler »



\pm&space;\sqrt(-5)^2-4\times&space;3\times&space;22\times&space;3=)

^2-4c2)


x-\fracx(x+2)x+2=x(x+2))
=\frac-12\pm&space;44-14)