Fraksjonelle ligninger
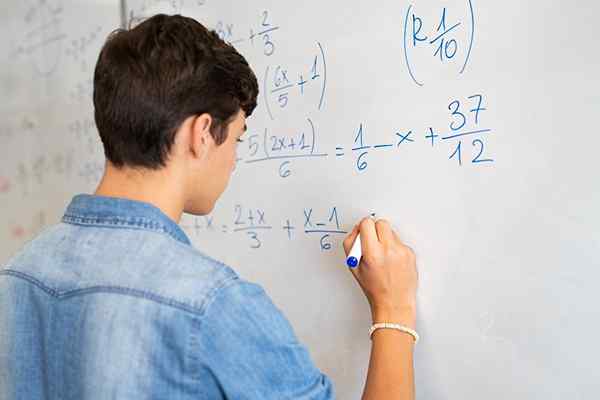
- 2398
- 534
- Mathias Aas
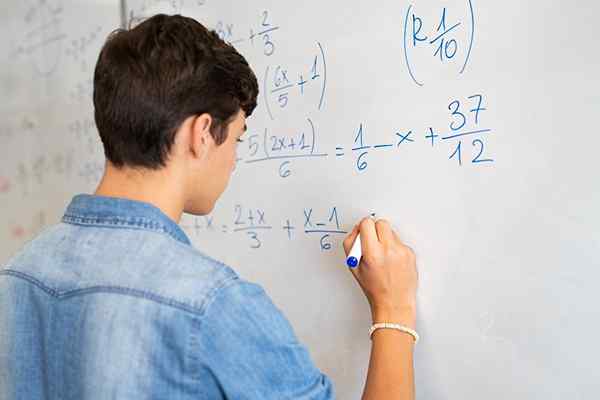 Fraksjonelle ligninger inkluderer numeriske og/eller algebraiske fraksjoner, og det ukjente kan være både i telleren og nevneren, eller begge deler
Fraksjonelle ligninger inkluderer numeriske og/eller algebraiske fraksjoner, og det ukjente kan være både i telleren og nevneren, eller begge deler Hva er brøkdelinger?
De fraksjonelle ligninger er de som inneholder brøk i en eller flere av deres vilkår. Slike brøk kan være numeriske eller algebraiske, der det ukjente finnes i telleren og/eller i nevneren til ethvert begrep.
Deretter noen eksempler på brøkdelinger med en enkelt ukjent:
Det første eksemplet er en lineær ligning med fraksjonelle koeffisienter; I det andre eksemplet er det ukjente i nevneren til hvert av vilkårene, og i det siste er det ukjente både telleren og i nevneren.
For å løse dem er det nødvendig å utføre noen algebraiske transformasjoner og dermed oppnå en ekvivalent ligning, der det ukjente ikke vises i nevneren. Når denne prosedyren er utført, blir løsningen funnet ved hjelp av passende teknikker.
Løsningen består av settet med "x" -verdier som tilfredsstiller likhet. Det kan være en unik verdi, eller flere, men i alle fall er det veldig viktig å huske på at ikke alle løsninger i den ekvivalente ligningen er akseptable med den opprinnelige ligningen.
Hvis det er en ligning hvis ukjent er i nevneren, må "X" -verdiene som annullerer, unngås, selv om de tilhører settet med ekvivalente ligningsløsninger. Dette er fordi inndelingen mellom 0 ikke er definert.
Hvis den ekvivalente ligningen har en unik løsning, og det viser seg at nevneren til noen av vilkårene i den opprinnelige ligningen blir kansellert, så har den ingen løsning.
Hvordan løse en brøkligning
Operasjonene som utføres for å løse ikke -fraksjonelle ligninger er gyldige, forutsatt at likhet opprettholdes. På denne måten, i en brøklig ligning, kan du legge til eller trekke fra samme mengde til begge sider av likhet, multiplisere alle begrepene med samme mengde, eller dele hvert begrep med samme mengde (forskjellig fra 0).
Kan tjene deg: Bolzano teoremMen siden brøkligningen er nødvendig for å transformere til en annen ekvivalent uten nevner, følges også følgende generelle indikasjoner:
- Finn det minste vanlige multiplum av nevner (m.c.m).
- Multipliser hvert begrep med m.c.m., For å eliminere nevner.
- Løs den ekvivalente ligningen oppnådd.
- Kontroller at løsningene som er funnet, tilfredsstiller den opprinnelige likheten.
Typer ekvivalente ligninger
De ekvivalente ligningene oppnådd etter den angitte prosedyren kan være:
- Lineær eller første grad
- Kvadratisk
- Av høyere orden
Løste eksempler
Eksempel 1
Løs følgende ligning:
Det bemerkes at ligningen er første grad i "x", ettersom "x" er høy på 1. Koeffisientene til ligningen er brøk og en måte å eliminere dem på, for å jobbe med hele tall, det multipliserer alle vilkårene med minimumsmultippet av nevner (m.c.m.).
m.c.m. (2,3,6) = 6
Så:
3x - 2x = 1
x = 1
Leseren kan sjekke gyldigheten av denne løsningen, erstatte x = 1 i den opprinnelige ligningen og bekrefte at en likhet oppnås.
Eksempel 2
Bestem “x” -verdiene som tilfredsstiller:
I motsetning til det forrige eksemplet, finnes det ukjente i dette tilfellet i nevneren. Merk at nevnerne er annullert for verdiene x = 2 og x = −1, en detalj som er praktisk å ta hensyn til, siden, hvis den ekvivalente ligningen innrømmer disse løsningene, må vi forkaste dem, siden de ikke er tillatt I den opprinnelige ligningen.
Nå må vi forvandle ligningen til en annen uten nevner, det første trinnet er å gjøre summen av vilkårene til venstre for likhet:
Ettersom nevnerne er de samme, slik at likestilling er oppfylt, er det nødvendig at tellerne også er:
Kan tjene deg: proporsjonalitetskonstant: hva er, beregning, øvelser4 (x+1) - 3 (x -2) = 8
Det er nok å løse denne ligningen, som viser seg å være første klasse:
4x + 4 - 3x + 6 = 8
x = 8 - 6 - 4 = - 2
x = - 2
Siden denne verdien er forskjellig fra de forbudte verdiene, blir den innrømmet som en løsning av den opprinnelige ligningen.
Eksempel 3
Finn løsningen på:
I denne ligningen avbryter verdien x = 4 nevnerne, derfor er den ekskludert fra løsningssettet til den transformerte ligningen, hvis den dukket opp.
Den transformerte ligningen er lett å finne, den er nok til å multiplisere alle begrepene med faktoren (x-4):
Blir:
2x - 4 = 4
2x = 8
x = 4
Eksempel 4
Løs ligningen:
I dette tilfellet har nevnerne kvadratiske vilkår, så det er praktisk å faktorere dem først:
- x2 + 8x + 7 = (x + 7) (x + 1)
- x2 - 49 = (x + 7) (x - 7)
- x2 - 6x - 7 = (x - 7) (x + 1)
Ligningen er slik:
Verdiene til x som avbryter noen av nevnerne er: x = −7, x = 7, x = −1. Derfor, selv om disse verdiene er en del av løsningssettet til den modifiserte ligningen, kan de ikke være en løsning av den opprinnelige ligningen.
Nå kommer prosessen med å transformere ligningen. Det første trinnet er å finne det minste vanlige multiplum av nevner:
m.c.m. = (x + 7) (x - 7) (x + 1)
Ved å multiplisere på begge sider av likhet med m.c.m. er til overs:
Resulterende:
(x --7) (x− 2) = (x + 1) (2x - 5) - (x + 7) (x - 2)
Gjennom distribusjonseiendommer er produktene utviklet:
x2 - 9x +14 = 2x2 - 3x - 5 - (x2 + 5x - 14)
Redusere lignende vilkår på høyre side:
x2 - 9x + 14 = x2 - 8x + 9
De kvadratiske vilkårene blir kansellert, ved å oppfylle det samme tegnet på forskjellige sider av likhet:
Kan tjene deg: Cubes Difference: Formler, ligninger, eksempler, øvelser- 9x + 14 = - 8x + 9
-x = -5 ⇒ x = 5
Dette resultatet er innrømmet som en løsning, siden det ikke er noen av de forbudte verdiene.
Bruk av utøvelse av brøkdelinger
Denominatoren av en brøkdel overstiger fire enheter til telleren. Hvis telleren trekkes fra telleren og nevneren også, er den resulterende brøkdelen 3/5. Bestem den opprinnelige brøkdelen.
Løsning
La X være verdien av telleren.
Siden brøkdelener overstiger fire enheter til telleren, er den opprinnelige brøkdelen:
Nå må du trekke fra 5 enheter, både til telleren og nevneren:
Siden brøkdelen som følge av å utføre den forrige prosedyren er lik 3/5, blir de utjevnet:
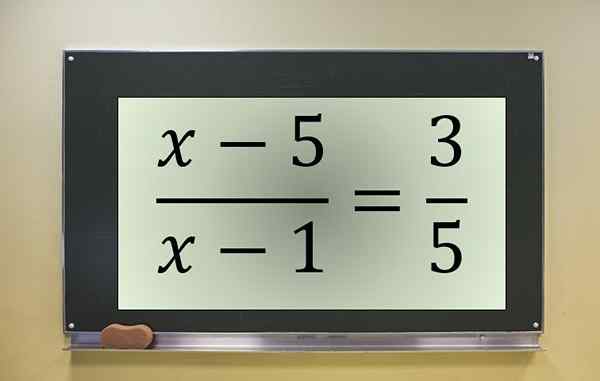 Fraksjonell ligningseksempel. Kilde: f. Zapata.
Fraksjonell ligningseksempel. Kilde: f. Zapata. Dette er en brøk ligning med den ukjente i teller og nevner, som blir kansellert ved x = 1. Derfor må denne verdien utelukkes, hvis den var blant løsningene av den transformerte ligningen.
Deretter multipliserer det begge sider med det minste felles multiplum, som er 5 (x - 1):
Noe som resulterer i følgende ekvivalente ligning:
5 (x - 5) = 3 (x - 1)
Bruke distribusjonseiendom:
5x -25 = 3x - 3 ⇒ 2x = 22
x = 11
Den opprinnelige brøkdelen erstatter x = 11 i uttrykket:
Noe som resulterer i brøkdel 11/15. Dette er svaret på problemet som reises.
Referanser
- Fraksjonelle ligninger. Gjenopprettet fra: Mathepower.com
- Matematikkportal. Fraksjonelle ligninger. Problemløsning. Gjenopprettet fra: Silvioduarte.com.
- Stewart, J. (2007). Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
- Sullivan, m. (1997). Forkalkning. 4. plass. Utgave. Pearson Education.
- Zill, d. (2008). Preccculment med fremskritt av beregning. 4. plass. Utgave. McGraw Hill.



(x+1))

=6\left%20(%20\frac16%20\right%20))
-3(x-2)(x-2)(x+1)=\frac8(x-2)(x+1))
\left%20(%20\fracxx-4%20\right%20)+(x-4)=(x-4)\left%20(%20\frac4x-4%20\right%20))

(x+1)=\frac2x-5(x+7)(x-7)-\fracx-2(x-7)(x+1))
(x-7)(x+1)\left%20[%20\fracx-2(x+7)(x+1)%20\right%20]=(x+7)(x-7)(x+1)\left%20[%20\frac2x-5(x+7)(x-7)-\fracx-2(x-7)(x+1)%20\right%20])



\left%20(%20\fracx-5x-1%20\right%20)=5(x-1)\frac35)