Doppler effektbeskrivelse, formler, tilfeller, eksempler

Han Doppler effekten Det er et fysisk fenomen som oppstår når mottakeren og kilden til bølger har relativ bevegelse, noe.

Hans navn skyldes den østerrikske fysikeren Christian Doppler (1803-1853), som beskrev og forklarte dette fenomenet i 1842, mens han presenterte et verk på fargen på doble stjerner, i en kongress av naturvitenskap i Praha, nåværende Tsjekkia.

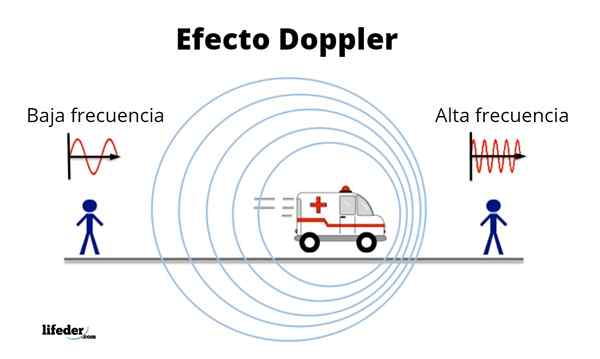
Illustrasjon av Doppler -effekten

[TOC]

Der Doppler -effekten blir presentert?

Figuren illustrerer en kilde til bølger som beveger seg fra venstre til høyre. En observatør foran kilden oppfatter korte bølgelengder og det motsatte for en observatør bak. Kilde: Wikimedia Commons.

Doppler -effekten presenteres i alle typer bølger, fra lysende til lyden, forutsatt at kilden og mottakeren beveger seg på hverandre. Og det er mye mer bemerkelsesverdig når den relative hastigheten mellom kilden og mottakeren er sammenlignbar med hastigheten på utbredelsen av bølgen.

Anta at en harmonisk bølge, som er en svingning som går videre i verdensrommet. Oscillasjonen gjentas med regelmessige tidsintervaller, denne gangen er begrepet og hans inverse frekvensen, Det er antall svingninger per tidsenhet. 

Når avstanden mellom kilden til den harmoniske bølgen og mottakeren forblir fast, oppfatter mottakeren den samme kildefrekvensen, det vil si at den registrerer samme antall pulser per tidsenhet som kilde. 

Imidlertid når mottakeren nærmer seg kilden med fast hastighet, kommer pulsen oftere. Og det motsatte oppstår når mottakeren beveger seg bort fra fast hastighet fra kilden: bølgepulser oppfattes med lavere frekvens.

Doppler Effektbeskrivelse

For å forstå hvorfor dette fenomenet skjer, vil vi bruke en analogi: to personer som spiller baller. Koppen får dem til å rulle i en rett linje på bakken mot partneren, som henter dem.

Hvis personen som lanserer sender en ball hvert sekund, vil den som samler dem, hvis den forblir fast, fange en ball hvert sekund. Alt bra så langt, siden det er forventet.

Bevegelsesresten

Anta nå at personen som fanger ballene er på et skateboard og bestemmer seg for å henvende seg til muggen med konstant hastighet. I dette tilfellet, når du skal møte ballene, vil du ha mindre enn et sekund mellom en ball og følgende.

Derfor ser mottakeren ut til å være mer enn en ball per sekund, det vil si frekvensen de når hånden hans økte. 

Det kan tjene deg: Fysikk under grekerne (Antige Hellas)

Det motsatte ville skje hvis den mottakende personen bestemte seg for å flytte bort fra utstederen, det vil si at ballenes ankomst ville øke med den påfølgende reduksjonen i frekvens som ballene ankommer.

Formler

Frekvensendringen beskrevet i forrige seksjon kan fås fra følgende formel:

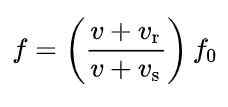
Her:

-F_enten Det er frekvensen av kilden.
-F er den tilsynelatende frekvensen i mottakeren.
-v er hastigheten (v> 0) for forplantning av bølgen i midten.
-v_r er hastigheten på mottakeren med hensyn til miljøet og
-v_s er hastigheten på kilden relatert til mediet.

Merk at v_r Det er positivt hvis mottakeren nærmer seg kilden og negativ ellers. På den annen side, v_s Det er positivt hvis kilden beveger seg bort fra mottakeren og negativ når den nærmer seg.

Kort sagt, hvis kilden og observatøren nærmer seg, øker frekvensen, og hvis de beveger seg bort, reduseres. Det motsatte skjer med den tilsynelatende bølgelengden i mottakeren (se oppgave 1).

Tilfeller der Doppler -effekten eksisterer

Kildehastighet og mottaker mye lavere enn bølgen

Det hender ofte at hastigheten på bølgen er mye større enn hastigheten som kilden eller hastigheten på bevegelsen til mottakeren beveger seg.

I dette tilfellet kan formelen tilnærmes på en slik måte at den er skrevet basert på den relative hastigheten til mottakeren (observatøren) med hensyn til kilden (e).

I dette tilfellet ville formelen være slik:

F = [1 + (VRS/V)] ⋅f_enten

Hvor v_Rs = v_r - v_s.

Når v_Rs Det er positivt (de nærmer seg), frekvensen f er større enn f_enten, Mens det er negativt (de beveger seg bort), er F mindre enn f_enten.

Relativ hastighetsdannende vinkel med den relative posisjonen

Den forrige formelen gjelder bare for tilfelle at kilden nærmer seg (eller flytter bort) direkte fra observatøren.

I tilfelle kilden beveger seg i å følge en tverrbane, er det nødvendig.

I dette tilfellet må vi søke:

F = [1 + (v_Rs ⋅ cos (θ) / v)] ⋅ f_enten

Igjen, en v_Rs Positivt tegn tilordnes hvis mottakeren og kilden nærmer seg, og negativ hvis den oppstår tvert imot.

Doppler -effekteksempler

Et daglig eksempel er sirenen til en ambulanse eller patrulje. Når vi nærmer oss er mer akutt, og når den beveger seg, er det mer alvorlig, spesielt forskjellen blir hørt på tidspunktet for maksimal tilnærming.

Det kan tjene deg: Fysisk bane: egenskaper, typer, eksempler og øvelser

En annen situasjon som forklares med Doppler -effekten er skiftet av spektrallinjene til stjernene mot blått eller rødt, hvis de nærmer seg oss, eller hvis de beveger seg bort. Dette kan ikke merkes med det blotte øye, men med et instrument som heter spektrometer.

applikasjoner

Doppler -effekten har mange praktiske applikasjoner, noen er listet opp nedenfor:

Radarer

Radarene måler avstanden og hastigheten som objektene som detekteres av den beveger seg og er basert nøyaktig på Doppler -effekten.

Radaren avgir en bølge mot objektet du vil oppdage, da reflekteres den bølgen tilbake. Tiden det tar før en puls å gå og retur tjener til å bestemme avstanden som objektet er. Og frekvensendringen i det reflekterte signalet gjør det mulig å vite om det aktuelle objektet beveger seg bort eller nærmer seg når radaren og hvor raskt.

Fordi radarbølgen går og kommer tilbake, er det en dobbel Doppler -effekt. I dette tilfellet er formelen som gjør det mulig å bestemme hastigheten på objektet med hensyn til radaren:

V_eller = ½ c ⋅ (Δf / f_enten)

Hvor:
-V_eller Det er hastigheten på objektet med hensyn til radaren.
-c hastigheten på den utsendte bølgen og reflekterte deretter.
-F_enten Radarutslippsfrekvensen.
-Δf frekvensforskyvningen, det vil si F - F_enten.

Astronomi

Takket være Doppler -effekten, er det bestemt at universet utvides, siden lysspekteret som sendes ut av fjerne galakser, forskyves mot rødt (en frekvensnedgang).

På den annen side er det også kjent at avgangshastigheten vokser i den grad de observerte galaksene er fjernere.

Ellers forekommer det med noen galakser av den lokale gruppen, det vil si naboene til vår Melkeveis.

For eksempel har vår nærmeste nabo, Andromeda Galaxy en blå økning (det vil si en økning i frekvensen) som indikerer at vi nærmer oss oss.

Doppler ultralyd

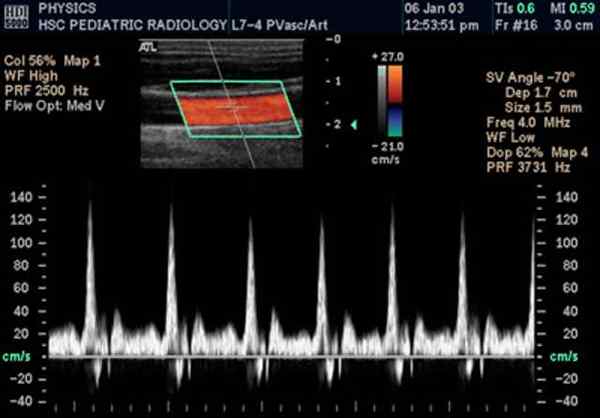Doppler ultralyd av halspulsåren. Kilde: Wikimedia Commons.

Det er en variant av det tradisjonelle økosonogrammet, der utnyttelse av Doppler -effekten Hastigheten på blodstrømmen i årer og arterier måles.

Øvelser

Oppgave 1 

Sirenen til en ambulanse har en frekvens er 300 Hz. Når du vet at lydhastigheten i luften er 340 m/s, må du bestemme bølgelengden til lyden i følgende tilfeller:

Det kan tjene deg: Kalibreringskurve: Hva er det for, hvordan du gjør det, eksempler

a) Når ambulansen er i ro.

b) Hvis du nærmer deg 108 km/t 

c) Ved å bevege seg bort i samme hastighet.

Løsning på

Det er ingen Doppler -effekt fordi både utstederen og kilden er i ro.

For å bestemme bølgelengden til lyden, er forholdet mellom frekvensen til F -enden F, bølgelengden λ på kilden og hastigheten på lyd V:

v = f_enten⋅λ.

Derfra følger det det:

λ = v / f_enten.

Derfor er bølgelengden:

λ = (340 m/s)/(300 1/s) = 1,13 m.

Løsning b

Mottakeren blir vurdert i ro, det vil si at V_r = 0. Emitteren er sirenen som beveger seg med hurtigheten av ambulansen:

v_s = (108/3,6) m/s = 30 m/s.

Den tilsynelatende frekvensen F er gitt av forholdet:

f = f_enten⋅ [(v + v_r)/(V + V_s)]

Bruk av denne formelen er oppnådd:

F = 300 Hz ⋅ [(340 + 0)/(340 - 30)] = 329 Hz.

Bølgelengden på mottakeren vil være:

λ_r= v / f = (340 m / s) / (329 1 / s) = 1,03 m.

Løsning c

Det løses på samme måte:

F = 300 Hz ⋅ (340 + 0)/(340 + 30) = 276 Hz.

Bølgelengden på mottakeren vil være:

λ_r = v / f = (340 m / s) / (276 1 / s) = 1,23 m.

Det konkluderes med at bølgefronter har en separasjon på 1,03 m når sirenen nærmer seg og 1,23 m når den beveger seg bort.

Oppgave 2

En karakteristisk linje med hydrogenemisjonsspekter.

Siden det er en økning i bølgelengden, vet vi at galaksen beveger seg bort. Hva er hastigheten din? 

Løsning

Kvotienten mellom forskyvningen av bølgelengden og hvilebølgelengden er lik kvotienten mellom hastigheten på galaksen og lysets hastighet (300.000 km/s). Så:

4/656 = 0.006

Derfor beveger galaksen seg fra 0.006 ganger lysets hastighet, det vil si 1800 km/s.

Referanser

1. Alonso - Finn. Vol -fysikk.2. 1970. Inter -American Education Fund, S.TIL. 
2. Baranek, l. 1969. Akustikk. 2. Utgave. McGraw Hill.
3. Griffiths g. Lineære og ikke -lineære bølger. Gjenopprettet fra: Scholarpedia.org.
4. Whitham G.B. 1999. Lineære og ikke -lineære bølger. Wiley. 
5. Wikiwaves. Ikke -lineære bølger. Gjenopprettet fra: wikiwaves.org
6. Wikipedia. Doppler effekten. Gjenopprettet fra: er.Wikipedia.com