Gravitasjonsenergiformler, egenskaper, applikasjoner, øvelser

De Gravitasjonsenergi Det er den som har et massivt objekt når det er nedsenket i gravitasjonsfeltet produsert av en annen. Noen eksempler på gjenstander med gravitasjonsenergi er: eplet i treet, eplet faller, månen som kretser rundt jorden og jorden som kretser rundt solen.

Isaac Newton (1642-1727) var den første som innså at tyngdekraften er et universelt fenomen, og at hvert objekt med masse produserer i miljøet et felt som er i stand til å produsere en styrke på en annen.

Figur 1. Månen som kretser rundt jorden har gravitasjonsenergi. Kilde: Pixabay

[TOC]

Formler og ligninger

Kraften referert til i Newton er kjent som gravitasjonskraft og gir energi til gjenstanden den fungerer. Newton formulerte den universelle gravitasjonsloven som følger:

"Vær henholdsvis to spesifikke masseobjekter M1 og M2, hver og en utøver på den andre en attraksjonskraft som er proporsjonal med produktet av massene deres og omvendt proporsjonal med kvadratet på avstanden som skiller dem.".

I forrige uttrykk, F Det er kraften i gravitasjonsattraksjonen som objekt 1 utøver på objekt 2 (eller omvendt), M1 og M2 De respektive massene av objekter og r er avstanden som skiller objekter. G Det er en konstant av proporsjonalitet kjent som gravitasjonskonstanten.

Gravitasjonsenergi ELLER assosiert med gravitasjonskraft F er:

Legg merke til tilstedeværelsen av et negativt tegn, noe som betyr at hvis skillet mellom objekter er begrenset, er gravitasjonsenergien negativ. Men hvis separasjonen har en tendens til uendelig, er gravitasjonsenergien null.

Et objekt som er nedsenket i et gravitasjonsfelt har gravitasjonspotensiell energi ELLER og kinetisk energi K. Hvis det ikke er andre interaksjoner, eller de er av ubetydelig intensitet, den totale energien OG Av dette objektet er summen av gravitasjonsenergien pluss den kinetiske energien:

E = k + u

Hvis et objekt er i et gravitasjonsfelt og andre dissipative krefter ikke er til stede, for eksempel friksjon eller luftmotstand, så total energi OG Det er en mengde som forblir konstant under bevegelse.

Kjennetegn på gravitasjonsenergi

- Et objekt har gravitasjonspotensiell energi hvis det bare er i nærvær av gravitasjonsfeltet produsert av en annen.

- Gravitasjonsenergien mellom to objekter vokser etter hvert som separasjonsavstanden mellom dem er større.

- Arbeidet utført av gravitasjonskraft er lik og i strid med variasjonen av gravitasjonsenergien i den endelige posisjonen med hensyn til den fra dens opprinnelige posisjon.

Det kan tjene deg: Hva er balansen i partikkelen? (Med eksempler)

- Hvis en kropp bare blir utsatt for virkningen av tyngdekraften, er variasjonen av gravitasjonsenergien lik og i strid med variasjonen av dens kinetiske energi.

- Den potensielle energien til et masseobjekt m i en høyde h Angående jordoverflaten er Mgh ganger større enn den potensielle energien på overflaten, å være g Akselerasjonen av tyngdekraften, for høyder h Mye lavere enn den jordiske radius.

Felt- og gravitasjonspotensial

Gravitasjonsfeltet g Det er definert som gravitasjonskraft F per masseenhet. Det bestemmes ved å plassere en testpartikkel på hvert punkt i rommet og beregne kvotienten mellom kraften som virker på testpartikkelen delt på verdien av dens masse:

g = F / m

Gravitasjonspotensialet V av et masseobjekt M som gravitasjonspotensialenergien til det objektet delt på sin egen masse er definert.

Fordelen med denne definisjonen er at gravitasjonspotensialet bare avhenger av gravitasjonsfeltet, slik at når potensialet er kjent V, Gravitasjonsenergi ELLER av et masseobjekt m er:

U = m.V 

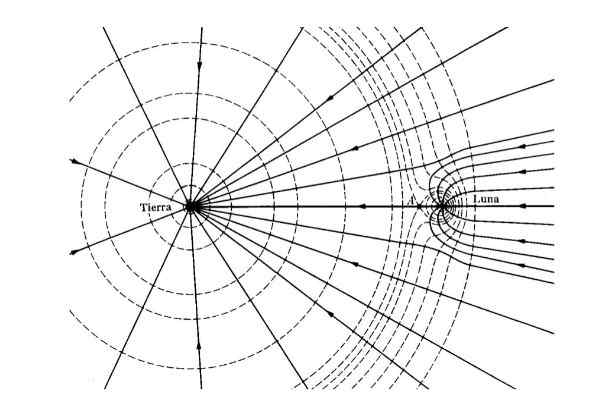Figur 2. Gravitasjonsfelt (kontinuerlige linjer) og Equi -Potensial (segmentert linje) for jorden - Luna System. Kilde: W T Scott, AM. J. Phys. 33, (1965).

applikasjoner

Gravitasjonspotensiell energi er det kroppene lagrer når de er i et gravitasjonsfelt.

For eksempel har vannet som er inneholdt i en tank mer energi i den grad tanken har høyere høyde.

Ved en høyere tank, desto større er vannløpshastigheten ved springen. Dette er fordi den potensielle vannenergien på høyden av tanken blir omgjort til kinetisk vannenergi ved utkanten av springen.

Når vannet er skadet på toppen av et fjell, kan den potensielle energien brukes til å rotere strømproduksjonsturbinene.

Gravitasjonsenergi forklarer også tidevann. Siden energi- og gravitasjonsstyrken avhenger av avstanden, er månens gravitasjonstrekk større i møte med landet nærmest månen enn det fjerneste og mest motsatte ansiktet.

Dette gir en forskjell i krefter som deformerer havoverflaten. Effekten er større på en ny måne, når solen og månen er på linje.

Muligheten for å bygge romlige og satellittstasjoner som forblir relativt nær planeten vår, skyldes gravitasjonsenergi produsert av jorden. Hvis ikke romstasjoner og kunstige satellitter ville vandre gjennom verdensrommet.

Det kan tjene deg: imantasjon: hva som består, metode og eksempler

Gravitasjonspotensialet til jorden

Anta at jorden har masse M og et objekt som er over jordoverflaten på avstand r Angående sentrum av det samme har en masse m. 

I dette tilfellet bestemmes gravitasjonspotensialet fra gravitasjonsenergi som bare deler seg mellom objektets masser som resulterer:

Gravitasjonspotensialet på jordoverflaten oppnås ved å erstatte r Av den terrestriske radius r_T. 

Potensiell energi nær jordoverflaten

Anta at jorden har radio R_T  og masse M.

Selv om jorden ikke er et rettidig objekt, tilsvarer feltet på overflaten det som vil bli oppnådd hvis all sin masse M Den var konsentrert i sentrum, slik at gravitasjonsenergien til et objekt i høyden H på jordens overflate er 

U (r_T + h) = -G.M m (r_T + h)^-1

Men fordi H er mye mindre enn r_T, Det forrige uttrykket kan nærme seg av 

U = uo + mgh

Hvor g er akselerasjonen av tyngdekraften, hvis gjennomsnittsverdi for jorden er 9.81 m/s^2.

Da er den potensielle energi -EPen til en masse m på høyden H på jordoverflaten:

EP (h) = u +uo = mgh

På jordens overflate h = 0, så et objekt på overflaten har EP = 0. Detaljerte beregninger kan sees i figur 3.

Figur 3. Gravitasjonspotensiell energi i en høyde H på overflaten. Kilde: Utarbeidet av F. Zapata.

Øvelser 

Oppgave 1: Gravitasjonsjord kollaps

Anta at planeten vår lider av en gravitasjonskollaps for tap av termisk energi inne og radius forfaller opptil halvparten av strømverdien, men planetens masse er konstant.

Bestem hva som vil være akselerasjonen av tyngdekraften nær overflaten av det nye landet og hvor mye en overlevende som veier 50 kg-f før kollapsen. Øker eller reduserer gravitasjonsenergien til personen og i hvilken faktor.

Løsning

Akselerasjonen av tyngdekraften på overflaten av en planet avhenger av dens masser og dens radius. Gravitasjonskonstanten er universell og tjener likt for planeter og eksoplaneter.

I tilfelle vi blir hevet, hvis jordens radius reduseres med halvparten, ville alvorlighetsgraden av det nye landet være 4 ganger større. Detaljene kan sees på neste styre.

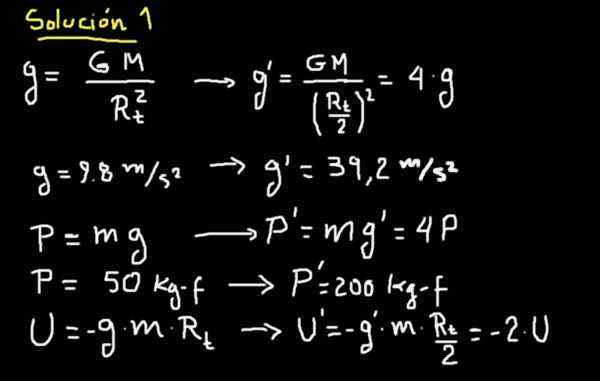
Dette betyr at en supermann og overlevende som på den gamle planeten veide 50 kg-f vil veie 200 kg-f på den nye planeten.

Kan tjene deg: Termisk balanse: Ligninger, applikasjoner, øvelser

På den annen side vil gravitasjonsenergien blitt redusert med halvparten på overflaten av den nye planeten.

Oppgave 2: Gravitasjonskollaps og rømningshastighet

I referanse til situasjonen som reises i oppgave 1, hva som ville skje med eksoshastigheten: øker, reduseres, i hvilken faktor?

Løsning 2

Eksoshastigheten er den minste hastigheten som er nødvendig for å unnslippe gravitasjonsattraksjonen til en planet.

For å beregne det antas det at et prosjektil som skyter med denne hastigheten når uendelig med null hastighet. I tillegg er gravitasjonsenergi i uendelig null null. Derfor vil et prosjektil som skyter med eksoshastigheten ha null total energi.

Det vil si at på overflaten av planeten på tidspunktet for skuddet må summen av den kinetiske energien til prosjektilet + gravitasjonsenergi være ugyldig:

½ m ve^2 - (g m.MR_T = 0

Merk at eksoshastigheten ikke avhenger av deigen til prosjektilet og dets kvadratiske verdi er

Ve^2 = (2g m) / r_T

Hvis planeten kollapser opp til en radius halvparten av originalen, blir torget til den nye eksoshastigheten dobbelt.

Derfor vokser den nye eksoshastigheten og blir 1.41 ganger den gamle rømningshastigheten:

Ve '= 1.41 Se

Oppgave 3: Apple gravitasjonsenergi

En gutt på balkongen på en bygning 30 meter fra bakken frigjør et eple på 250 g, som etter noen sekunder når bakken.

Figur 4. Mens du faller, blir eplens potensielle energi forvandlet til kinetisk energi. Kilde: Pixabay.

a) Hva er gravitasjonsenergiforskjellen på eplet øverst på eplet på jordnivå?

b) Hvor raskt spredte eplet seg rett før det spredte seg på bakken?

c) Hva med energi når eplet knuste mot bakken? 

Løsning

a) Forskjellen i gravitasjonsenergi er 

m.g.H = 0.250 kg * 9.81 m/s^2 * 30 m = 73.6 J

b) Den potensielle energien som eplet hadde da det var 30 m høy, blir omdannet til kinetisk energi for når eplet når bakken.

½ m v^2 = m.g.h

V^2 = 2.g.h

Ved å erstatte verdier og rydding, følger det at eplet når bakken med en hastighet på 24.3 m/s = 87.3 km/t.

c) Det er klart at eplet er spredt og all gravitasjonsenergi som akkumuleres i begynnelsen går tapt i form av varme, siden eplestykkene og påvirkningssonen blir oppvarmet, i tillegg er en del av energien også spredt i form av lydbølger "Splash".

Referanser

1. Alonso, m. (1970). Vol -fysikk. 1, interamerikansk utdanningsfond. 
2. Hewitt, Paul. 2012. Konseptuell fysisk vitenskap. 5. plass. Ed. Pearson.
3. Knight, r. 2017. Fysikk for forskere og ingeniørfag: En strategitilnærming. Pearson.
4. Sears, f. (2009).University Physics Vol. 1 
5. Wikipedia. Gravitasjonsenergi. Gjenopprettet fra: er.Wikipedia.com
6. Wikipedia. Gravitasjonsenergi. Hentet fra: i.Wikipedia.com