Mekaniske energiformler, konsept, typer, eksempler, øvelser

De mekanisk energi av et objekt eller system er definert som summen av dens potensielle energi og dens kinetiske energi. Som navnet tilsier, skaffer systemet mekanisk energi takket være virkningen av mekaniske krefter som vekt og elastisk kraft.

I henhold til mengden mekanisk energi som kroppen har, vil den også ha muligheten til å utføre et mekanisk arbeid.

Figur 1. Roller Mountain Car -bevegelsen kan beskrives ved bevaring av mekanisk energi. Kilde: Pixabay.

Energien - typen som er - er en skalær mengde, og mangler derfor retning og mening. Være OG_m Den mekaniske energien til et objekt, ELLER dens potensielle energi og K Dens kinetiske energi, formelen for å beregne den er:

OG_m = K + u

Enheten i det internasjonale energisystemet av noe slag er Joule, som er forkortet som J. 1 j tilsvarer 1 n.m (Newton per meter).

Når det gjelder kinetisk energi, beregnes den som følger:

K = ½ m.v²

Hvor m Det er massen til objektet og v Dens hastighet. Kinetisk energi er alltid en positiv mengde, siden massen og kvadratet med hastigheten er. Når det gjelder potensiell energi, hvis det handler om gravitasjonspotensiell energi, har du:

U = m.g.h

Her m Det er fremdeles deigen, g Det er akselerasjonen av tyngdekraften og h Det er høyden med hensyn til referansenivået eller hvis det er foretrukket, bakken.

Nå, hvis den aktuelle kroppen har elastisk potensiell energi -kan det være en fjær -det er fordi den er komprimert eller kanskje langstrakt. I så fall er den tilhørende potensielle energien:

U = ½ kx²

Med k som fjærkonstanten, som indikerer hvor enkelt eller vanskelig det er å deformere den og x Lengden på nevnte deformasjon.

[TOC]

Konsept og egenskaper ved mekanisk energi

Utdyping av definisjonen gitt før, mekanisk energi avhenger da av energien forbundet med kroppsbevegelse: kinetisk energi, pluss bidraget til potensiell energi, som som vi sa kan være gravitasjon, på grunn av vekt og vekt og posisjon som opptar kroppen med Respekt til jord eller referansenivå.

La oss illustrere dette med et enkelt eksempel: Anta at du har en gryte på gulvet og i ro. Siden det er fortsatt, har den ingen kinetisk energi, og den er også på bakken, et sted der det ikke kan falle; Derfor mangler det gravitasjonspotensial energi og dens mekaniske energi er 0.

Anta at noen plasserer gryten like ved kanten av et tak eller et vindu, klokka 3.0 meter høy. For dette måtte personen gjøre en jobb mot tyngdekraften. Potten har nå gravitasjonspotensiell energi, den kan falle fra den høyden og dens mekaniske energi er ikke lenger ugyldig.

Figur 2. En gryte på toppen av et vindu har gravitasjonspotensiell energi. Kilde: Pixabay.

Under disse omstendighetene har potten OG_m = U Og denne mengden avhenger av pottens høyde og vekt, som angitt før.

La oss si at potten faller fordi den var i en prekær posisjon. Når hastigheten øker og med den kinetiske energien, mens gravitasjonspotensial energi avtar, fordi den mister høyden. Den mekaniske energien når som helst av høsten er:

Kan tjene deg: Hva er de avledede størrelsene?

OG_m = U + k = ½ m.v² + m.g.h  

Konservative og ikke-konservative krefter

Når potten er i en viss høyde, har den gravitasjonspotensiell energi fordi hvem klatret den, gjorde en jobb mot tyngdekraften. Størrelsen på dette arbeidet er verdt det samme som det som lager tyngdekraften når potten faller av Fra samme høyde, men det har det motsatte tegnet, siden det ble laget mot det.

Arbeidet som krefter som tyngdekraft og elastisitet avhenger bare av startposisjonen og den endelige posisjonen ervervet av objektet. Uansett bane fulgte for å gå fra en til en annen, bare selve verdiene betyr noe. Kreftene som oppfører seg på denne måten kalles Konservative krefter.

Og ettersom de er konservative, lar de arbeidet som er gjort av dem lagres som potensiell energi i konfigurasjonen av objektet eller systemet. Det er grunnen til at potten på kanten av vinduet eller taket hadde muligheten for å falle, og med den for å utvikle bevegelse.

På den annen side er det krefter hvis verk avhenger av banen etterfulgt av objektet de handler. Friksjonen tilhører denne typen krefter. Sko Sol vil bli brukt mer når du går fra et sted til et annet på en vei med mange omganger, enn når du går for en annen direkte.

Friksjonskrefter gjør en jobb som reduserer kroppens kinetiske energi, fordi den bremser dem ned. Og det er grunnen til at den mekaniske energien til systemene som friksjonen fungerer, har en tendens til å avta.

En del av arbeidet som er gjort med makt, går tapt av varme eller lyd, for eksempel.

Typer mekanisk energi

Mekanisk energi er, som vi sa, summen av kinetisk energi og potensiell energi. Nå kan potensiell energi komme fra forskjellige konservative krefter: vekt, elastisk styrke og elektrostatisk kraft.

- Kinetisk energi

Kinetisk energi er en skalær mengde som alltid blir bevegelsen. Enhver partikkel eller bevegelig objekt har kinetisk energi. Et objekt som beveger seg i en rett linje har kinetisk oversettelse av kinetisk energi. Det samme skjer hvis det roterer, i dette tilfellet er det snakk om rotasjonskinetisk energi.

For eksempel har en bil som beveger seg langs en vei kinetisk energi. Også en fotballball mens han beveger seg langs banen eller personen som går raskt for å nå kontoret.

- Potensiell energi

Det er alltid mulig å knytte en skalarfunksjon som kalles potensiell energi til en konservativ styrke. Følgende skilles ut:

Gravitasjonspotensiell energi

Den som alle objekter har i kraft av deres høyde med hensyn til bakken, eller referansenivået som er valgt som sådan. Som et eksempel har noen som er i ro på terrassen til en 10 -etasjers bygning, potensiell energi 0 med hensyn til terrassen, men ikke med hensyn til gaten som er 10 etasjer under.

Elastisk potensiell energi

Det lagres vanligvis i objekter som ligaer og fjærer, assosiert med deformasjonen de opplever når de strekker seg eller komprimerer dem.

Elektrostatisk potensiell energi

Det lagres i et system med elektrisitetsbelastninger i likevekt, på grunn av den elektrostatiske interaksjonen mellom dem. Anta at det er to elektriske ladninger av det samme separate tegnet på en liten avstand; Ettersom elektriske kostnader for det samme tegnet blir frastøtt, forventes det at en ekstern agent har gjort arbeid for å bringe dem nærmere.

Kan tjene deg: vekslende strømkretser: Typer, applikasjoner, eksempler

Når det er plassert, klarer systemet å lagre arbeidet som agenten gjorde for å konfigurere dem, i form av elektrostatisk potensiell energi.

Bevaring av mekanisk energi

Tilbake til den fallende potten, blir gravitasjonspotensialenergien den hadde da den var på kanten av taket forvandlet til kinetisk bevegelsesbevegelse. Dette øker på bekostning av den første, men summen av begge forblir konstant, siden pottens fall aktiveres av tyngdekraften, som er en konservativ kraft.

Det er en utveksling mellom en type energi og en annen, men den opprinnelige mengden er den samme. Derfor er det gyldig å bekrefte det:

Innledende mekanisk energi = endelig mekanisk energi

OG_{Innledende m} = E_{M Final}

Alternativt:

K_første + ELLER_første = K _endelig + ELLER_endelig

Med andre ord endres ikke mekanisk energi og endres og ∆E_m = 0. "∆" -symbolet betyr variasjon eller forskjell mellom en endelig mengde og en initial.

For å anvende prinsippet om bevaring av mekanisk energi til problemløsning er det nødvendig å:

-Det gjelder bare når kreftene som virker på systemet er konservative (alvorlighetsgrad, elastisk og elektrostatisk). I så fall: ∆E_m = 0.

-Studiesystemet må isoleres. Det er ingen energioverføring på noen måte.

-Hvis det dukker opp i et problem med å bli falt, da ∆E_m ≠ 0. Likevel kan problemet løses ved å finne arbeidet utført av konservative krefter, siden det er årsaken til reduksjonen i mekanisk energi.

Fradrag for mekanisk energibesparing

Anta at en konservativ styrke virker på systemet som gjør en jobb W. Dette arbeidet forårsaker en endring i kinetisk energi:

W = ∆K (Cinetic Work-Energy Theorem)

Det er viktig å merke seg at arbeidsenergi-teoremet kinetisk er aktuelt selv når det gjelder ikke-konservative krefter.

På den annen side er arbeidet også ansvarlig for endringen i potensiell energi, og i tilfelle av en konservativ styrke er endringen i potensiell energi definert som det negative av dette arbeidet:

W = -∆u

Matcher disse ligningene, siden begge refererer til arbeidet som er gjort på objektet:

∆K = -∆u 

K_F - K_enten = -(u_F - ELLER_enten)

Abonnement symboliserer "endelig" og "initial". Gruppering:

K_F + ELLER_F = K_enten + ELLER_enten                                                    

Eksempler på mekanisk energi

Mange objekter har komplekse bevegelser, der det er komplisert å finne uttrykk for posisjon, hastighet og akselerasjon som en funksjon av tiden. I slike tilfeller er anvendelse av det mekaniske energibesparelsesprinsippet en mer effektiv prosedyre enn å prøve å anvende Newtons lover direkte.

La oss se på noen eksempler der mekanisk energi bevares:

-En skiløper som glir nedoverover på snødekte åser, forutsatt at fravær av friksjon antas. I dette tilfellet er vekten den forårsakende kraften til bevegelsen gjennom hele banen.

-Russiske fjellvogner, Det er et av de mest typiske eksemplene. Her er også vekten kraften som definerer bevegelse og mekanisk energi bevares hvis det ikke er noen friksjon.

Kan tjene deg: ioniseringsenergi

-Den enkle pendelen Det består av et masse som er underlagt et uutholdbart tau -det endrer ikke lengden -som kort skiller seg fra vertikalen og får lov til å svinge. Vi vet at det til slutt vil stoppe på grunn av friksjon, men når friksjonen ikke blir vurdert, blir også mekanisk energi bevart.

-En blokk som påvirker en vår Fikset i den ene enden på veggen, alle på et veldig glatt bord. Blokken komprimerer fjæren, reiser en viss avstand og blir deretter avfyrt i motsatt retning, fordi fjæren strekker seg. Her skaffer blokken sin potensielle energi takket være arbeidet som gjør våren på den.

-Vår og ball: Når en fjær er komprimert av en ball, denne sprett. Dette skyldes at når våren frigjøres, blir potensiell energi kinetisk energi i ballen.

-Trampolinehopp: Det fungerer som en vår, og promoterer personen som hopper på ham elastisk. Dette benytter seg av vekten når den hopper, som den deformerer trampolinen, men denne, når den kommer tilbake til sin opprinnelige posisjon, gir impulsen til genseren.

Figur 3. Springbrettet fungerer som en vår, og promoterer menneskene som hopper på den. Kilde: Pixabay.

Løste øvelser

- Oppgave 1

Et masseobjekt M = 1 kg slippes med en rampe fra en høyde på 1 m. Hvis rampen er ekstremt glatt, beregner du kroppshastigheten akkurat når fjæren kolliderer.

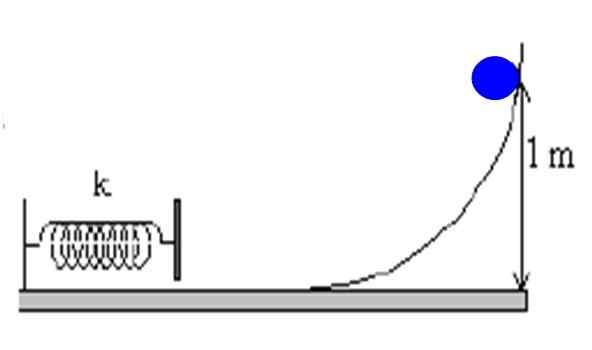Figur 4. Et objekt synker på en rampe uten friksjon og komprimerer en fjær som er festet til veggen. Kilde: f. Zapata.

Løsning

Uttalelsen rapporterer at rampen er jevn, noe som betyr at den eneste kraften som virker på kroppen er dens vekt, en konservativ kraft. Dermed indikeres det å anvende bevaring av mekanisk energi mellom noen punkter i banen.

Tenk på punktene merket i figur 5: A, B og C.

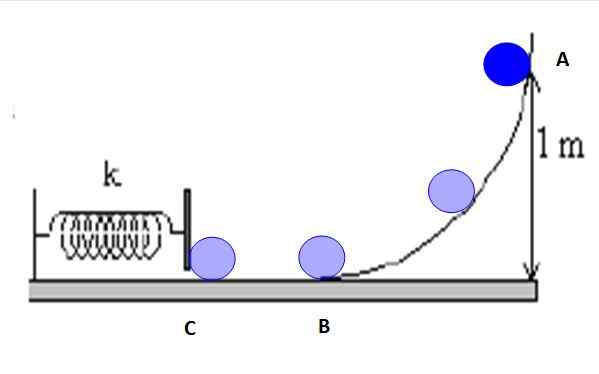Figur 5. Stien som følger objektet er friksjon og mekanisk energi bevares mellom et par punkter. Kilde: f. Zapata.

Det er mulig å etablere bevaring av energi mellom A og B, B og C eller A og C, eller noen av mellompunktene på rampen. For eksempel mellom A og C har du:

Mekanisk energi ved A = mekanisk energi i C

OG_ma = E_MC

K_TIL + ELLER_TIL = K_C + ELLER_C

½ m.v_TIL² + m.g.h_TIL = ½ m V_C² + m.g.h_C

Som utgitt fra punkt A, hastigheten V_TIL = 0, derimot h_C = 0. I tillegg blir massen kansellert, fordi det er en vanlig faktor. Så:

g.h_TIL = ½ v_C²

v_C²= 2 g.h_TIL

- Oppgave 2

Finn den maksimale komprimeringen som vårens fjær løst 1 vil oppleve, hvis den elastiske konstanten av den samme er 200 n/m.

Løsning

Den elastiske konstanten av fjæren indikerer kraften som skal påføres for å deformere en lengdeenhet. Siden konstanten av denne våren er verdt k = 200 n/m, indikerer dette at 200 n er nødvendig for å komprimere eller strekke den 1 m.

Være x Avstanden som objektet komprimerer fjæren før den stopper ved punkt D:

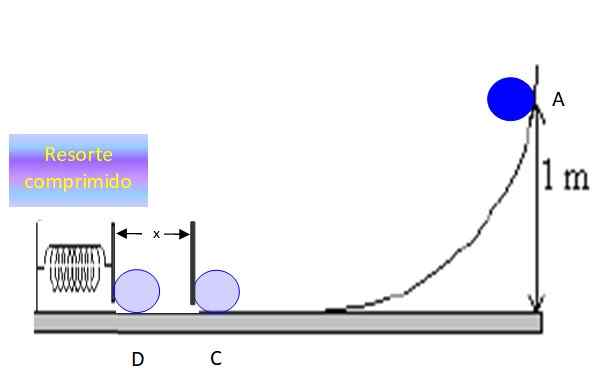Figur 6. Objektet komprimerer fjæren en x -avstand og stopper øyeblikkelig. Kilde: f. Zapata.

Bevaring av energi mellom punktene C og D, fastslår at:

K_C + ELLER_C = K_D + ELLER_D

På punkt C har den ikke gravitasjonspotensiell energi, siden høyden er 0, men den har kinetisk energi. I D har han stoppet helt, derfor er det K_D = 0, men i stedet har du til disposisjon den potensielle energien til den komprimerte fjæren u_D.

Bevaring av mekanisk energi gjenstår:

K_C = U_D

½ mv_C² = ½ kx²

 

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
2. Figueroa, d. 2005. Serier: Fysikk for vitenskap og ingeniørfag. Volum 1. Kinematikk. Redigert av Douglas Figueroa (USB).
3. Knight, r.  2017. Fysikk for forskere og ingeniørfag: En strategitilnærming. Pearson.
4. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1.
5. Wikipedia. Mekanisk energi.Gjenopprettet fra: er.Wikipedia.org.