Ustabilt balansekonsept og eksempler

I mekanikk er et objekt i Ustabil balanse Når den ved å flytte den bare fra sin posisjon med makt, kommer den ikke tilbake til den. For eksempel er ballen til følgende figur, når den er over haugen i ustabil likevekt, fordi den minste forstyrrelse vil gjøre den opp ned, uten muligheten for å returnere med sine egne midler.

Figur 1. Ballen er i ustabil likevekt i venstre plassering, i likegyldig balanse i sentrum og i stabil balanse til høyre. Kilde: Wikimedia Commons.

På den annen side, når ballen er på en flat overflate, som i sentrums posisjon, sies det at den er i likegyldig balanse eller nøytral. En styrke som forstyrrer den kan påføres, og flytter den til en annen side, men hvis styrken forsvinner, vil ballen være stabil igjen.

Til slutt, til høyre, er ballen i bunnen av en konkav bolle. Denne stillingen er også balansert, men Stabil balanse. En styrke som forstyrrer ballen, vil bare få den til å svinge litt rundt den opprinnelige posisjonen, for å ende opp med å komme tilbake til den.

[TOC]

Årsaker til tap av balanse

Vanlige gjenstander (og mennesker og dyr) mister balansen og faller på grunn av dreiemomentet som stammer fra vekten, kraften utøvd av jorden over alle gjenstander nær overflaten. Når du har en utvidet kropp, kalles punktet der vekten virker Gravity Center.

Vekten kan balanseres takket være støtte, for eksempel den som gir en overflate, og på denne måten vil ikke objektet bevege seg. Men har fortsatt muligheten til å snu med hensyn til et eller annet punkt, for i utvidede objekter er ikke balansen mellom styrkene den eneste faktoren for å holde dem stille, men også stedet der disse kreftene blir brukt.

Nedenfor er det en figur med en balansert blyant på spissen, i ustabil balanse. Enhver luftstrøm vil slå den ut, men i mellomtiden blir normalvekten og kraften som støtter seg kompensert. I tillegg har begge kreftene samme handlingslinje, og dette går gjennom blyantens spiss, og sikrer balanse.

Kan tjene deg: Ikke -koplanære vektorer: Definisjon, forhold, øvelser

Men hvis blyanten lener seg bare litt, som vist til høyre, slutter vektenes linje å passere gjennom spissen, som fungerer som en pivot. Deretter produserer vekten et ikke -balansert dreiemoment og blyanten dreier seg i retning av klokkehender.

Figur 2. Blyanten som støttes på spissen er i ustabil likevekt, vil en liten forstyrrelse føre til at vekten produserer et dreiemoment med hensyn til spissen og blyanten vil falle. Kilde: f. Zapata.

Faktorer som garanterer stabilitet

Nesten alltid det som søkes er den stabile balansen, siden den ustabile balansen er, som navnet indikerer, ganske prekær. Fortsetter med blyanets eksempel, når den faller og forblir horisontalt på overflaten, er den nye posisjonen mye mer stabil enn da den ble stoppet på spissen.

Dette fordi tyngdekraften på den ene siden er nærmere overflaten, og på den andre siden er støtteoverflaten på blyanten mye større.

Når støtteflaten er LAR. Og hvis avstanden fra tyngdepunktet til overflaten er lavere, er vektspakarmen lavere, og derfor er dreiemomentet også.

Avslutningsvis, jo større grunnlag for støtte til objektet, og nærmere tyngdepunktet til gulvet, jo mindre har sannsynligheten for å velte, og balansen har en tendens til å være stabil. Babyer vet det, og det er derfor de vanligvis knekker først før de risikerer å stå.

Og hvis i stedet for å bli støttet, er kroppen suspendert fra et punkt, har plasseringen av tyngdepunktet også en fremtredende rolle når du etablerer balanse, som det vil bli sett kort tid i følgende eksempler.

Kan tjene deg: Mount Olympus (Mars)

Balanseeksempler

Balanse i støttede kropper

Balansen i de støttede kroppene avhenger, som nevnt, av:

-Hvor nær tyngdepunktet i overflaten.

-Objektbasestørrelsen.

Tenk på en kjegle på et flatt bord. Den mest stabile posisjonen uten tvil er med basen av kjeglen som er fullt støttet på bordet. Dette er den stabile likevektsposisjonen, siden tyngdepunktet til kjeglen er på symmetriaksen og nærmere basen enn spissen.

Den likegyldige balansen oppnås ved å plassere kjeglen og den ustabile balansen tilsvarer kjeglen på spissen, for eksempel blyanten, som kanskje ikke er en enkel oppgave, gitt at den minste bevegelsen kjeglen svinger.

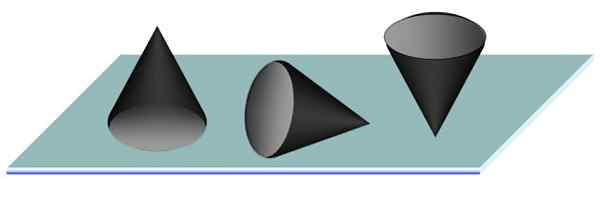Figur 3. Stabil, likegyldig og ustabil balanse av en kjegle støttet på et bord. Kilde: f. Zapata.

Balanse i suspenderte kropper

Det er vanlig å finne suspenderte kropper som henger minst ett punkt, for eksempel malerier og lamper. Når du etablerer balansen, er det nødvendig å vurdere plasseringen av tyngdepunktet og suspensjonspunktet.

Situasjonen er lett å visualisere ved hjelp av et rektangulært pappark eller en homogen materialregel. Her sammenfaller tyngdepunktet med det geometriske sentrum av figuren, som antar at massen til objektet er fordelt jevn.

For å plassere arket i ustabil likevekt, er det suspendert fra et punkt som finnes under Fra tyngdepunktet holder det bare arket mellom fingrene uten å stramme for mye, for å etterlate ham bevegelsesfrihet.

En liten kraft er nok til at arket umiddelbart kan rotere i en eller annen forstand. Årsaken til svingen er den samme som i tilfelle av det støttede objektet: vekten utøver et kompromissløst dreiemoment som letter rotasjonen av kroppen.

Kan tjene deg: Løsningsvarme: Hvordan det beregnes, applikasjoner og øvelser

Ved sving passerer arket gjennom en stilling som er av stabil likevekt, der suspensjonspunktet gjenstår ovenfra av tyngdepunktet. Rundt denne stillingen varierer den litt og stopper til slutt.

Hvis en kraft blir påført igjen, varierer laminaen igjen, men går tilbake til den posisjonen igjen, der suspensjonspunktet og tyngdepunktet er på linje med vertikalen.

Til slutt blir den likegyldige balansen sjekket ved å passere en pinne nettopp gjennom tyngdepunktet. Hvis arket er snudd for å holde seg i forskjellige posisjoner, ser det at det ikke vil være større forskjell mellom dem.

Avslutningsvis, for kroppene som er suspendert i ustabil likevekt, er suspensjonspunktet under tyngdepunktet. Og det motsatte for stabil balanse.

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
2. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6. Ed Prentice Hall.
3. Hewitt, Paul. 2012. Konseptuell fysisk vitenskap. 5. plass. Ed. Pearson.
4. Resnick, r. (1999). Fysisk. Vol. 1. 3. utg. på spansk. Continental Editorial Company s.TIL. Av c.V.
5. Rex, a. 2011. Fundamentals of Physics. Pearson.
6. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1. Pearson.