Rotasjonsbalanseformler og ligninger, eksempler, øvelser

Det hevdes at et utvidet legeme er i Rotasjonsbalanse Når summen av dreiemomentene som virker på den er null. Dette betyr ikke at objektet nødvendigvis er i ro, men heller at det ikke er noen netttrend som endrer bevegelsestilstand til en annen.

Et objekt som beveger seg med konstant hastighet gjør det langs en rett linje, og vi kan vurdere det i rotasjonsbalanse. Nå dreier gjenstander fordi det er krefter som handler på dem på en slik måte at det er en rotasjon. En krafts evne til å produsere rotasjon, kalt dreiemoment eller Torca, Det avhenger ikke bare av styrkenes intensitet, men også hvor den brukes.

Figur 1. Figurens hengebro ble designet for å være i rotasjonsbalanse. Kilde: Wikimedia Commons.

Vi kjenner igjen dette umiddelbart når en lukket dør kommer til å åpne: styrken blir aldri brukt i nærheten av hengslene, men langt fra dem, så håndtaket er plassert så langt som mulig, ved siden av døren til døren.

Hengslene passerer døren til døren. Insisterer på å skyve den veldig nær hengslene, må du gjøre en stor innsats for at døren til og med beveger seg litt.

I litteraturen er dreiemomentet med forskjellige navn: Torsjonsøyeblikk, torsjon, øyeblikk av en styrke og Torca. Alle er synonymer.

Så vi må kjenne dreiemomentene som virker på et objekt for å etablere rotasjonsbalansetilstanden.

[TOC]

Rotasjonsbalansetilstand

Rotasjonsbalansetilstanden er:

Summen av alle øyeblikkene eller dreiemomentene som virker på et legeme, beregnet med hensyn til en hvilken som helst akse, må være ugyldig.

Det aktuelle objektet må utvides, siden partikler per definisjon bare har oversettelsesbalanse.

Du kan tjene deg: Newtons andre lov: søknader, eksperimenter og øvelser

Det kan være påførte krefter på kroppen, og det er fremdeles en rotasjonsbalanse, mens kreftene ikke snur den.

Det kan også være bevegelse, til og med akselerert, men alltid langs en rett linje, siden ikke alle krefter forårsaker utseendet til moment. Disse vises når kreftene ikke opptrer hele samme handlingslinje.

Dreiemoment eller kraftmoment

Dreiemomentet er betegnet med de greske tekstene τ, i Fet skrift Fordi det er en vektor og vi skiller den fra størrelsen eller modulen, som er en skalar. Det avhenger av den påførte kraften F, av vektoren r som er rettet fra rotasjonsaksen eller til anvendelsespunktet og til slutt, av vinkelen mellom disse to vektorene.

Det rette forholdet mellom disse størrelsene er etablert gjennom vektorproduktet:

τ = r x F

Og momentmodulen, betegnet uten fet skrift er:

τ = r⋅f⋅sen θ

Hvor θ er vinkelen mellom r og F. Momentenheter er ganske enkelt n⋅m i det internasjonale systemet.

I figuren er det en engelsk nøkkel som den er ment. For dette blir to krefter prøvd F_TIL og F_B.

F_TIL er nærmere O og har en vektor r_TIL eller kortere spakarm, produserer derfor ikke så mye dreiemoment og kraft F_B, Som har samme størrelse, men den har en vektor r_B større.

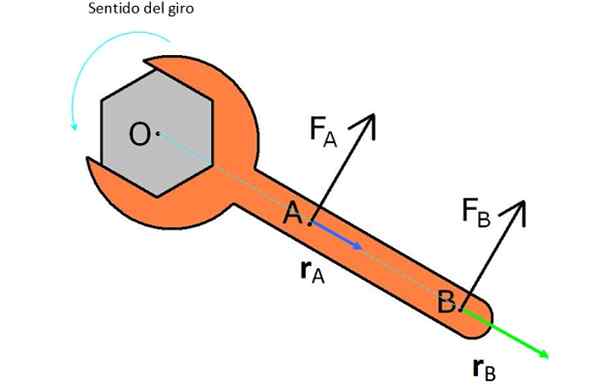Figur 2. Krefter og armer påført en engelsk nøkkel for å vri den i strid med klokken nåler. Kilde: Wikimedia Commons.

Merk at hvis du vil rotere mutteren i en plan, må du bruke kreftene i motsatt retning av hvordan de vises på figuren.

Retning og følelse av dreiemoment

Ettersom dreiemomentet er resultatet av kryssproduktet mellom styrke- og posisjonsvektorene, og disse er i planet til den engelske nøkkelen, må dreiemomentet være en vektor vinkelrett på det planet, det vil si rettet mot leseren eller inne i siden.

Kan tjene deg: Atmosfærisk trykk: Normal verdi, hvordan det måles, eksempler

Ved konvensjon er dreiemomentet positivt hvis det produserer sving i motsatt retning av klokken nåler, og negativt hvis det gjør det i retning av klokken.

Retningen og retningen til det resulterende dreiemomentet bestemmes lett av regelen for høyre hånd vist nedenfor:

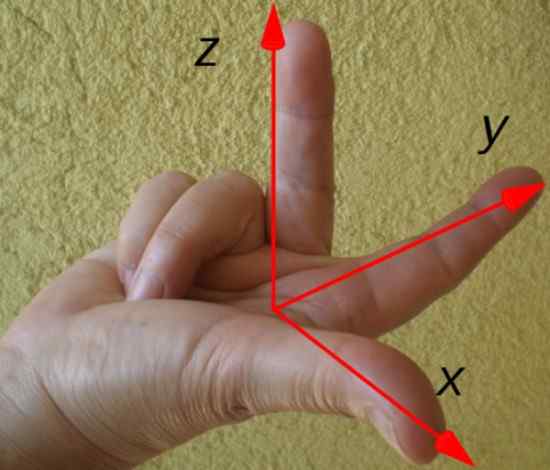Figur 3. Høyre håndregel for å bestemme retningen og retningen til troca. Kilde: Wikimedia Commons.

Pekefingeren peker i henhold til posisjonsvektoren r, Langfingeren i henhold til kraft F Og tommelen signaliserer retningen og retningen på dreiemomentet τ. I dette eksemplet er dreiemomentet rettet langs x -aksen, i henhold til tegningen av koordinataksene.

Formler og ligninger

Hvis dreiemomentene virker på et legeme τ₁, τ_2, τ_{3 ..} τ_Yo, Nettet eller det resulterende dreiemomentet τ_n Det er vektorsummen av dem alle:

τ_n = τ₁+ τ₂ +  τ₃ +_.. τ_Yo

Med summering av summering gjenstår det:

τ_n = ∑ τ_Yo

Likevektstilstanden uttrykkes matematisk som følger:

τ_n = 0

O vel:

∑ τ_Yo = 0

Hvor dreiemomentet τ, Når det gjelder en viss o -akse, beregnes den av:

τ = r x F

Og hvis størrelse er:

τ = r⋅f⋅sen θ

Eksempler

-Hos mennesker og dyr er vekt en kraft som kan forårsake dreiemoment og svinge og falle.

Folk opprettholder vanligvis en slik posisjon at når de går, holder dem i rotasjonsbalanse, med mindre sportsaktivitet praktiseres, for eksempel gymnastikk, skøyter eller sport generelt.

-To barn som klarte å holde seg horisontalt i Rocker enten opp og ned De er i rotasjonsbalanse.

-Når balansen er balansert, er systemet i rotasjons likevekt.

-Varsler og trafikklys som henger på gater og veier er også i rotasjonsbalanse. Hvis kablene som holder dem er ødelagte, går denne balansen tapt og varselet henger eller faller.

Det kan tjene deg: Gjennomsnittlig akselerasjon: Hvordan den beregnes og løses

-Hengende broer som Golden Gate i San Francisco og broen på figur 1.

Trening løst

Baren støttet av en støtte vist på figuren er veldig lys. Kraften utøvd av støtte er F Og på slutten gjelder styrken TIL.

Det blir bedt om å beregne størrelsen på disse kreftene med tanke på at systemet er i balanse mellom oversettelse og rotasjon.

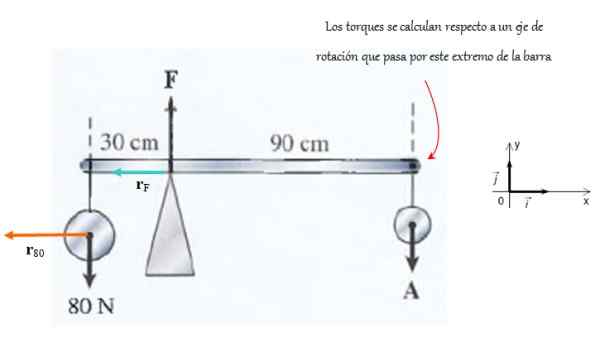Figur 4. På denne barstyrken opptrer på en slik måte at den forblir i rotasjons likevekt. Kilde: f. Zapata.

Løsning

Ettersom systemet ikke beveger seg, blir summen av krefter kansellert. Alle er vertikale, og du kan jobbe med størrelsesorden. Den positive sansen er oppe og den negative ned, derfor:

F - 80 - a = 0

Nå brukes rotasjons likevektstilstanden, som du må velge en vilkårlig rotasjonsaks. I dette tilfellet er det valgt på slutten til høyre, slik at vektoren r_TIL Være null, på denne måten dreiemomentet som utøves av TIL, Men bare de av F og styrken til venstre.

Dreiemomentet produsert av F Det er i henhold til regelen for høyre og koordinatsystemet som er vist:

τ_F = r_F x F = 0.9 F (-k) N.m

Det er rettet på skjermen og har et negativt tegn. Mens dreiemomentet produsert av kraften på 80 N er:

τ = 80 x 1.tjue (k) N⋅m = 96 (k) N⋅m

Dette dreiemomentet er rettet ut av skjermen og tildeles et positivt tegn. Ettersom det er rotasjonsbalanse:

96 - 0.9⋅f = 0

Størrelsen på F er:

F = (96/0.9) n = 106.7 n

Og siden systemet er i oversettelsesbalanse, blir summen av kreftene kansellert. Dette lar oss fjerne størrelsen på TIL:

F - a - 80 n = 0

Derfor:

A = 106.7 - 80 n = 26.7 n.

Referanser

1. Rex, a. 2011. Fundamentals of Physics. Pearson.
2. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning.
3. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1. Pearson.
4. Tipler, s. (2006) Fysikk for vitenskap og teknologi. 5. utg. Volum 1. Redaksjon tilbake.
5. Tippens, p. 2011. Fysikk: konsepter og applikasjoner. 7. utgave. McGraw Hill.