Termiske likevektsligninger, applikasjoner, øvelser

Den termiske balansen mellom to kropper som er i termisk kontakt er staten som oppnås etter lenge nok tid, slik at temperaturene til begge kroppene er lik.

I termodynamikk blir termisk kontakt av to kropper (eller to termodynamiske systemer) forstått som en situasjon der kroppene har mekanisk kontakt eller skilles, men i kontakt med en overflate som bare tillater varmepassering fra den ene kroppen til den andre (diatermisk overflate ).

Figur 1. Etter en stund vil isen og drinken nå sin termiske balanse. Kilde: Pixabay

Ved termisk kontakt skal det ikke være noen kjemisk reaksjon mellom systemene i kontakt. Det skal bare være varmeutveksling.

Hverdagssituasjoner der det er varmeutveksling blir presentert for systemer som kald drikke og glass, varm kaffe og teskje, eller kropp og termometeret, blant mange andre eksempler.

[TOC]

Når to eller flere systemer er i termisk likevekt?

Den andre loven om termodynamikk slår fast at varmen alltid går fra den høyeste temperaturlegemet til den laveste temperaturen. Varmeoverføring opphører så snart temperaturene er utjevnet og den termiske likevektsstatusen er nådd.

Den praktiske anvendelsen av termisk likevekt er termometeret. Et termometer er en enhet som måler sin egen temperatur, men takket være termisk balanse kan vi kjenne temperaturen til andre kropper, for eksempel en person eller et dyr.

Kvikksølvkolonnettermometeret er plassert i termisk kontakt med kroppen, for eksempel under tungen, og nok er det forventet at nok tid vil nå den termiske balansen mellom kroppen og termometeret, og at avlesningen ikke varierer mer.

Når dette punktet er nådd, er termometeremperaturen den samme som kroppen.

Nullloven for termodynamikk slår fast at hvis et legeme A er i termisk likevekt med en kropp C og den samme kroppen C er i termisk likevekt med B, så er A og B i termisk likevekt, selv når mellom A og B er ingen termisk kontakt.

Vi konkluderer med at to eller flere systemer er i termisk likevekt når de har samme temperatur.

Termiske likevektsligninger

Vi antar at et legeme ved starttemperatur i termisk kontakt med en annen B -kropp med initialtemperatur TB. Vi antar også at TA> TB, i henhold til den andre loven overføres varmen fra A til B.

Etter en stund vil den termiske balansen nås, og begge kroppene vil ha samme endelige temperatur TF. Dette vil ha en mellomverdi til TA og TB, det vil si TA> TF> TB.

Mengden varme overført fra A til B vil være Qa = Ma Ca (tf - TA), der Ma er massen av kropp A, Ca varmekapasiteten per enhetsmasse på en y (TF - TA) temperaturforskjellen. Hvis TF er mindre enn da er QA negativ, noe som indikerer at kroppen gir varme.

Tilsvarende for kropp B må du QB = MB CB (TF - TB); Og hvis TF er større enn TB, er QB positiv, noe som indikerer at kroppen B mottar varme. Ettersom kropp A og B er i termisk kontakt mellom dem, men isolert fra miljøet, skal den totale mengden utvekslet varme være null: QA + QB = 0

Deretter MA CA (TF - TA) + MB CB (TF - TB) = 0

Balansetemperatur

Utvikling av dette uttrykket og rydde TF -temperaturen oppnås den endelige termiske likevektstemperaturen.

Figur 2. Endelig balansetemperatur. Kilde: Selvlaget

TF = (MA CA TA + MB CB TB) / (MA CA + MB CB).

Som et spesielt tilfelle, bør du vurdere saken om at organer A og B er identiske i masse og i varmekapasitet, i dette tilfellet vil likevektstemperaturen være:

Tf = (ta + tb) / 2 ↔ hvis ma = mb og ca = cb.

Termisk kontakt med faseendring

I noen situasjoner skjer det at når to kropper er plassert i termisk kontakt, forårsaker varmeutvekslingen endring av tilstand eller fase i en av dem. Hvis dette skjer, må det tas i betraktning at det i løpet av faseendringen ikke er noen temperaturendring i kroppen som endrer statusen.

Hvis faseendringen av et av kroppene i termisk kontakt oppstår, brukes konseptet med latent varme l, som er energien per masseenhet som er nødvendig for tilstandsendringen:

Q = l ∙ m

For eksempel, for å smelte 1 kg is ved 0 ° C, er 333,5 kJ/kg påkrevd, og den verdien er den latente isens smeltedeling.

Under fusjonen skiftes fast vann til flytende vann, men at vannet opprettholder den samme istemperaturen under fusjonsprosessen.

applikasjoner

Termisk balanse er en del av dagliglivet. La oss for eksempel undersøke denne situasjonen i detalj:

-Oppgave 1

En person ønsker å bade med varmt vann ved 25 ° C. Plasser på et kube 3 liter kaldt vann ved 15 ° C og i kjøkkenet varmet varmevann opp til 95 ° C.

Hvor mange liter varmt vann må legge til den kalde vannkuben for å ha ønsket slutttemperatur?

Løsning

Anta at det er kaldt vann og B varmt vann:

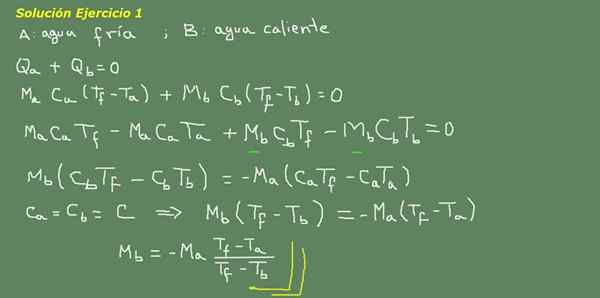Figur 3. Oppgave 3 -løsning. Kilde: Selvlaget.

Vi foreslår den termiske likevektsligningen, som indikert på tavlen i figur 3 og derfra tømmer vi MB -vannet.

Den innledende massen av kaldt vann kan oppnås fordi tettheten av vannet er kjent, som er 1 kg for hver liter. Det vil si at vi har 3 kg kaldt vann.

Ma = 3 kg

Så

MB = - 3 kg*(25 ° C - 15 ° C)/(25 ° C - 95 ° C) = 0,43 kg

Da er det nok med 0,43 lt varmt vann å endelig oppnå 3,43 liter varmt vann ved 25 ° C.

Løste øvelser

-Oppgave 2

Et stykke metall på 150 g masse blir introdusert og med 95 ° C temperatur til en beholder som inneholder en halv liter vann ved en temperatur på 18 ° C. Etter en stund er den termiske balansen og temperaturen på vannet og metallet nådd 25 ° C.

Anta at beholderen med vann og metallstykke er en lukket termos som ikke tillater varmeutveksling med miljøet.

Få den spesifikke metallvarmen.

Løsning

Først vil vi beregne varmen som er absorbert av vann:

QA = MA CA (TF - TA)

QA = 500g 1cal/(g ° C) (25 ° C - 18 ° C) = 3500 kalorier.

Det er den samme varmen gitt av metall:

QM = 150g cm (25 ° C - 95 ° C) = -3500 kalorier.

Da kan vi få varmekapasiteten til metallet:

Cm = 3500 cal/ (150g 70 ° C) = ⅓ cal/ (g ° c).

Øvelse 3

Du har 250 C.c. vann ved 30 ° C. Til det vannet som er i en isolerende termos, tilsettes 25g isbiter ved 0 ° C, med det formål å avkjøle det.

Bestem likevektstemperaturen; det vil si at temperaturen som vil forbli når all isen har smeltet og isvannet har varmt opp til vannet som opprinnelig hadde glasset.

Løsning 3

Denne øvelsen kan løses i tre trinn:

1. Den første er fusjon av is som absorberer varme fra det første vannet for å smelte og bli vann.
2. Deretter beregnes temperaturen reduksjon i det innledende vannet, fordi det har gitt varme (QCED<0) para fundir el hielo.
3. Til slutt må smeltet vann (fra is) være termisk balansert med vannet som eksisterte i utgangspunktet.

Figur 4. Oppgave 3 -løsning. Kilde: Selvlaget.

La oss beregne varmen som er nødvendig for fusjon av is:

QF = L * MH = 333,5 kJ/kg * 0,025 kg = 8,338 kJ

Deretter er varmen tildelt av vannet for å smelte isen qced = -QF

Denne varmen tildelt av vannet synker temperaturen til en T '-verdi som vi kan beregne som følger:

T '= t0 - qf/(ma*ca) = 22,02 ° C

Hvor Ca er vannkapasiteten til vann: 4,18 kJ/(kg ° C).

Endelig vil den opprinnelige massen av vann som nå er ved 22,02 ° C gi varme til det smeltede vannet fra isen som er ved 0 ° C.

Til slutt vil likevektstemperaturen oppnås etter nok tid:

Te = (ma * t ' + mH * 0 ° C) / (ma + mh) = (0,25 kg * 22,02 ° C + 0,025 kg * 0 ° C) / (0,25 kg + 0,025 kg).

Til slutt oppnå likevektstemperaturen:

TE = 20,02 ° C.

-Oppgave 4

Et blystykke på 0,5 kg etterlater ovnen ved en temperatur på 150 ° C, som er ganske under smeltepunktet. Det stykket er plassert i en beholder med 3 liter vann ved romtemperatur på 20 ° C. Bestem den endelige likevektstemperaturen.

Beregn også:

- Mengde varme levert av bly til vann.

- Mengde varme absorbert av vann.

Data:

Spesifikk blyvarme: CP = 0,03 kalk/(g ° C); Spesifikk vannvarme: Ca = 1 kalk/(g ° C).

Løsning 

For det første bestemmer vi den endelige likevektstemperaturen TE:

TE = (MA CA TA + MP CP TP) / (MA CA + MP CP)

TE = 20,65 ° C

Da er mengden varme tildelt av bly:

QP = MP CP (TE - TP) = -1,94 x 10³ Lime.

Mengden varme som er absorbert av vann vil være:

QA = Ma Ca (TE - TA) = +1.94x 10³ Lime.

Referanser

1. Atkins, p. 1999. Fysisk kjemi. Omega -utgaver.
2. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
3. Giancoli, d. 2006. Fysikk: Prinsipper med applikasjoner. 6. ... Ed Prentice Hall.
4. Hewitt, Paul. 2012. Konseptuell fysisk vitenskap. 5. plass. Ed. Pearson.
5. Resnick, r. (1999). Fysisk. Vol. 1. 3. utg. på spansk. Continental Editorial Company s.TIL. Av c.V.
6. Rex, a. 2011. Fundamentals of Physics. Pearson.
7. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1.
8. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning.