Tilfeldig feilformel og ligninger, beregning, eksempler, øvelser

Han Tilfeldig feil av en fysisk mengde består av de ikke -forutsigbare variasjonene av målet på det beløpet. Disse variasjonene kan produseres av fenomenet som måles, av måleinstrumentet eller av observatøren selv.

Slik feil skyldes ikke at noe er gjort galt under eksperimentet, men at det er en feil som ligger i måleprosessen eller fenomenet som er studert. Dette forårsaker tiltaket som er målt noen ganger litt større og noen ganger litt lavere, men svinger vanligvis rundt en sentral verdi.

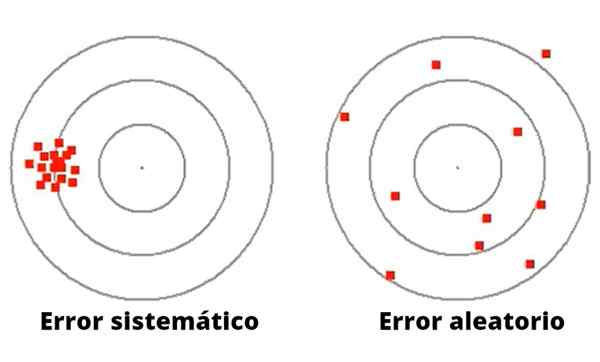
Figur 1- Tilfeldige feil varierer i størrelse og retning. Tvert imot, systematiske feil har en tendens til å være konsistente.

I motsetning til tilfeldig feil, kan systematisk feil være forårsaket av dårlig kalibrering eller en upassende skalafaktor i måleinstrumentet, inkludert en svikt i eksperimentelt utstyr, eller en upassende observasjon, som forårsaker et avvik i samme forstand.

Figur 1 illustrerer forskjellen mellom systematisk og tilfeldig feil i DART -lanseringsspillet til et mål med sirkler.

I tilfelle av venstre er dartene konsentrert rundt en veldig langt fra sentrum. Koppen til disse dartene, selv om de er av godt mål, har en systematisk fiasko, kanskje av visuell opprinnelse, eller i veien for å kaste.

På den annen side har muggen til høyre (i figur 1) en stor spredning rundt det sentrale målet, derfor er det en veldig upresis pitcher, med et dårlig mål, som ufrivillig gjør tilfeldig feil.

[TOC]

Formler og ligninger i tilfeldig feil

Når måleprosessen viser tilfeldig feil, er det nødvendig.

I hver måling er det selvfølgelig nødvendig å passe på at forholdene de utføres alltid er de samme.

Kan tjene deg: Faraday Law: Formula, Units, Experimenter, Exercise,

Anta at målingen gjentas n ganger. Ettersom det er tilfeldig feil i hver måling, vil det være en litt annen verdi. Anta at settet med n Målinger er:

x₁, x₂, x₃,..., x_n

Så hvilken verdirapport for tiltak? 

Gjennomsnittlig verdi og standardavvik

De mellomverdi enten gjennomsnitt av settet med tiltak, som vi betegner med og beregnes som følger:

= (x₁ + x₂ + x₃ +… +X_n) / n

Standardavvik

Dette resultatet har imidlertid en feilmargin gitt av standardavviket. For å definere det, må du først kjenne avviket og deretter variansen:

-Avviket d_Yo  at hver målte verdi har Xi Angående gjennomsnittsverdien er:

d_Yo = x_Yo -

Hvis gjennomsnittet av avvikene ble beregnet, ville det bli oppnådd systematisk = 0, gitt at: 

= (d₁ + d₂ + d₃ +… +D_n) /n =

= [x₁ - ) + (x₂ - ) +… +(X_n - )]/n

= (x₁+ x₂ +… + X_n) / n - n / n = - = 0

-Gjennomsnittet av avvik er ikke nyttig å kjenne spredningen av tiltakene. På den annen side er gjennomsnittsverdien av kvadratet med avvik eller varians, betegnet med σ², Ja, det er det.

Det beregnes i henhold til følgende formel:

σ² = (d₁² + d₂² +.. .+ d_n² ) / (N -1)

I statistikk kalles dette beløpet forskjell.  

Og ved kvadratroten av variansen er det kjent som Standardavvik σ:

σ = √ [(d₁² + d₂² +.. .+ d_n² ) / (n -1)] 

Standardavviket σ indikerer at:

1.- 68% av målingene som er gjort er inkludert i intervallet [ - σ, + σ]. 

2.- 95% av målingene er i intervallet [ - 2σ, + 2σ].

3.- 99,7% av tiltakene er i området [ - 3σ, + 3σ].

Hvordan beregne tilfeldig feil?

Målingsresultatet er mellomverdi av n Målinger betegnet med og beregnet i henhold til følgende formel:

Kan tjene deg: areolar hastighet: hvordan den beregnes og løses øvelser

= (∑x_Yo) / n

Det er imidlertid ikke den "nøyaktige" verdien av målingen, siden den påvirkes av Tilfeldig feil ε, som beregnes slik:

ε = σ / √n

Hvor:

σ = √ [(∑ (xi -)² ) / (n -1)]

Det endelige resultatet av målingen må rapporteres på noen av følgende måter:

1. ± σ / √n = ± ε Med 68% konfidensnivå.
2. ± 2σ / √n = ± 2ε Med 95% konfidensnivå.
3. ± 3σ / √n = ± 3ε Med 99,7% konfidensnivå.

Den tilfeldige feilen påvirker den siste signifikante figuren av målingen, som vanligvis sammenfaller med forståelsen av måleinstrumentet. Imidlertid, hvis den tilfeldige feilen er veldig stor, kan de to siste viktige sifrene påvirkes av variasjon.

Tilfeldige feileksempler

Tilfeldige feil kan vises i forskjellige tilfeller der et tiltak blir gjort:

Måling av en lengde med et målebånd eller regel

Når en lengde måles med en regel eller et målebånd og avlesningene faller mellom skalaene i skalaen, er den mellomverdien estimert estimert.

Noen ganger har estimatet overflødig og annen feil, så tilfeldig feil blir introdusert i måleprosessen.

Figur 2. Tilfeldige feil kan vises når en lengde måles med et tape tape. Kilde: Pikrepo.

Vindens hastighet

I måling av vindens hastighet kan det være endringer i lesing fra et øyeblikk til et annet, på grunn av fenomenets skiftende natur.

Når du leser volumet i en gradert sylinder

Når volumet leses med en gradert sylinder, til og med å prøve å minimere parallage -feilen, hver gang den måles, endres den menisk -observasjonsvinkelen litt, og det er grunnen til at tiltakene blir påvirket av tilfeldig feil.

Det kan tjene deg: Første likevektstilstand: Forklaring, eksempler, øvelser Figur 3.- I kjemilaboratoriet er det mulig å gjøre tilfeldige feil ved å lese en kandidatsylinder. Kilde: Pexels.

Når et barn blir målt

Ved å måle høyden på et barn, spesielt hvis det er litt rastløs, gjør det at små holdningsendringer er litt endring av lesing.

Når du bruker baderomsskalaen

Når vi ønsker å måle vekten vår med et bad, en liten endring i støttepunktet, kan til og med en posisjonsendring tilfeldig påvirke målingen.

Trening løst

En leketøys barnevogn har lov til å rulle langs et rett og skrå spor og målt med stoppeklokke tiden som tar hele sporet. 

Målingen gjøres 11 ganger, med omsorg for å slippe vogna fra samme sted, uten å gi noen impuls og beholde hellingens fikser.

Settet med oppnådd resultater er:

3.12s 3.09s 3.04s 3.04s 3.10s 3.08s 3.05s 3.10s 3.11s 3.06s, 3.03s

Hva er den tilfeldige feilen i tiltakene?

Figur 4. Tar tiden til en leketøystreng som går ned gjennom et skrå fly. Kilde: Fanny Zapata.

Løsning

Som det fremgår, er resultatene som er oppnådd ikke unike og varierer litt.

Den første er å beregne gjennomsnittlig nedstigningstidsverdi, og få 3.074545455 sekunder.

Det gir ingen mening å opprettholde så mange desimaler, siden hver måling har tre viktige tall og den andre desimalen av hvert tiltak er usikker, siden det er på grensen for takknemlighet for stoppeklokken, derfor er resultatet avrundet til to desimaler:

= 3,08 s.

Med kalkulatoren i statistisk modus er standardavviket σ = 0,03 s Og standardfeilen er σ / √11 = 0,01 s. Det endelige resultatet er uttrykt som følger:

Nedstigningstid 

3,08 s ± 0,01s (med 68%konfidensnivå)

3,08 s ± 0,02s (med 95%konfidensnivå)

3,08 s ± 0,03s (med 99,7%konfidensnivå)

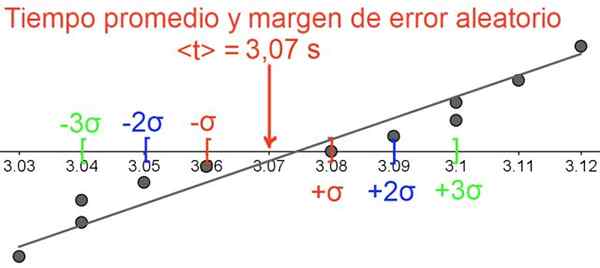Figur 5. Den tilfeldige feilmarginen, merk at dataene er gruppert rundt gjennomsnittsverdien. Kilde: f. Zapata.

Referanser

1. Canavos, g. 1988. Sannsynlighet og statistikk: applikasjoner og metoder. McGraw Hill.
2. Devore, J. 2012. Sannsynlighet og statistikk for ingeniørfag og vitenskap. 8. Utgave. Cengage.
3. Helmestine a. Tilfeldig feil Vs. Systematisk feil. Gjenopprettet fra: Thoughtco.com
4. Laredo, e. Mellomfeil. Gjenopprettet fra: USB.gå.
5. Levin, r. 1988. Statistikk for administratorer. 2. Utgave. Prentice Hall.