Inverse trigonometriske funksjoner, avledet, eksempler, øvelser

De Inverse trigonometriske funksjoner, Som navnet tilsier, er de de tilsvarende inverse funksjonene til bihule, kosinus, tangent, cotangent, tørking og høstfunksjoner.

Inverse trigonometriske funksjoner er betegnet med samme navn på den tilsvarende direkte trigonometriske funksjonen pluss prefikset BUE. Dermed:

1.- Arcsen (x) Det er den omvendte trigonometriske funksjonen til funksjonen Sin (x)

2.- Arccos (x) Det er den omvendte trigonometriske funksjonen til funksjonen cos (x)

3.- Arctan (x) Det er den omvendte trigonometriske funksjonen til funksjonen Tan (x)

4.- Arccot ​​(x) Det er den omvendte trigonometriske funksjonen til funksjonen barneseng (x)

5.- Arcsec (x) Det er den omvendte trigonometriske funksjonen til funksjonen sek (x)

6.- Arccsc (x) Det er den omvendte trigonometriske funksjonen til funksjonen CSC (x)

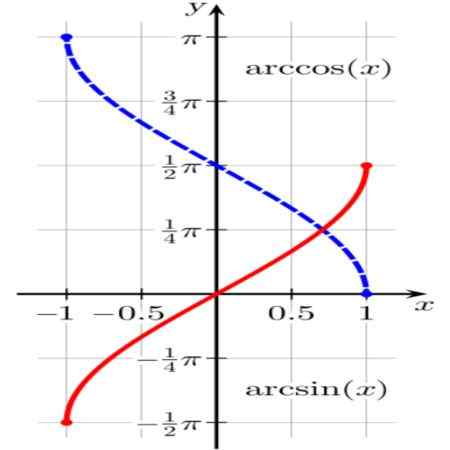
Figur 1. Arcsen -funksjoner (x) (i rødt) og Arccos (x) (i blått). Kilde: Wikimedia Commons.

Funksjonen θ = Arcsen (x) Det resulterer i en enhetsbue θ (eller vinkel i radianer θ) slik at sin (θ) = x.

Således, for eksempel Arcsen (√3/2) = π/3 siden som kjent er brystet til π/3 -radianer lik √3/2.

[TOC]

Hovedverdien av inverse trigonometriske funksjoner

Slik at en matematisk funksjon f (x) har omvendt G (x) = f^-1(x) Det er nødvendig at denne funksjonen er Injeksjon, Noe som betyr at hver verdi og ankomstsettet med funksjonen f (x) kommer fra en og bare en X -verdi.

Det er tydelig at dette kravet ikke blir oppfylt av noen trigonometrisk funksjon. For å avklare poenget, la oss legge merke til at verdien y = 0,5 kan oppnås fra bihulefunksjonen på følgende måter:

• sin (π/6) = 0,5
• sin (5π/6) = 0,5
• sin (7π/6) = 0,5

Og mange flere, siden bihulefunksjonen er periodisk med periode 2π.

Det kan tjene deg: Multipler av 8: Hva er og forklaring

For å definere inverse trigonometriske funksjoner, er det nødvendig å begrense domenet til deres tilsvarende direkte trigonometriske funksjoner, slik at de oppfyller injeksjonskravet.

Dette begrensede domenet med direkte funksjon vil være hovedområdet eller grenen av den tilsvarende inverse funksjonen.

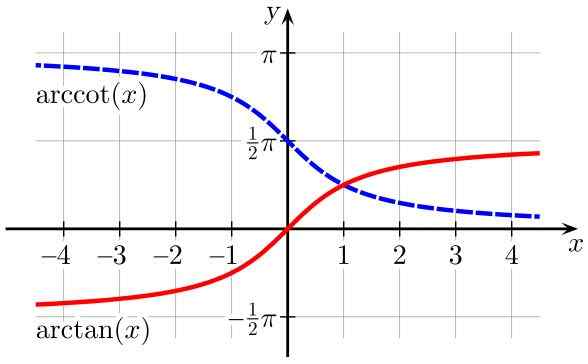Figur 2. Arctan -funksjoner (x) (i rødt) og Arccot ​​(x) (i blått). Kilde: Wikimedia Commons.

Tabell over domener og områder av inverse trigonometriske funksjoner

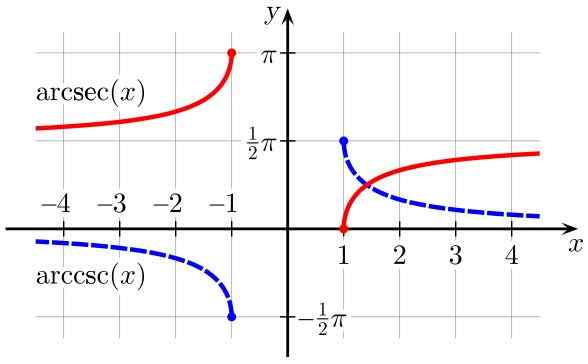Figur 3. Arcsec (x) (i rødt) og ARCCSC (x) (i blå) funksjoner (i blått). Kilde: Wikimedia Commons.

Avledet fra inverse trigonometriske funksjoner

For å oppnå derivater av de inverse trigonometriske funksjonene, brukes egenskapene til derivatene, spesielt den som er avledet fra en omvendt funksjon.

Hvis vi betegner for f (y) til funksjonen og med f^-1(x) til sin inverse funksjon, er da avledet fra omvendt funksjon relatert til derivatet av direkte funksjon gjennom følgende forhold:

[F^-1(x)] '= 1/ f' [f^-1(x)]

For eksempel: Hvis x = f (y) = √y er den direkte funksjonen, vil dens inverse være

y = f^-1(x) = x². La oss anvende regelen om det omvendte derivatet til denne enkle saken for å se at denne regelen er oppfylt:

[x²] '= 1 / [√y]' = 1 / (½ og^-½ = 2 og^½ = 2 (x²)^½ = 2x 

Vel, vi kan vurdere dette trikset for å finne de som er avledet fra inverse trigonometriske funksjoner.

For eksempel tar vi θ = Arcsen (x) Som den direkte funksjonen vil den inverse funksjonen være sin (θ) = x.

[Arcsen (x)] '= 1 / [sin (θ)]' = 1 / cos (θ) = 1 / √ (1 - sen (θ)²) = ..

... = 1 / √ (1 - x²) .

På denne måten kan alle de som er avledet fra de inverse trigonometriske funksjonene oppnås, som er vist nedenfor:

Figur 4. Tabell over de som er avledet fra inverse trigonometriske funksjoner. Kilde: Wikimedia Commons.

Disse derivatene er gyldige for ethvert z -argument som tilhører komplekse tall og er derfor også gyldige for ethvert reelt argument x, siden z = x + 0i.

Kan tjene deg: firkantet: elementer, egenskaper, klassifisering, eksempler

Eksempler

- Eksempel 1

Finn Arctan (1).

Løsning

Arctan (1) er enhetsbuen (vinkelen i radianer) ፀ slik at brunfargen (ፀ) = 1. Den vinkelen er ፀ = π/4 fordi så (π/4) = 1. Deretter arctan (1) = π/4.

- Eksempel 2

Beregn Arcsen (cos (π/3)).

Løsning

Vinkelen π/3 radianer er en bemerkelsesverdig vinkel hvis kosinus er ½, slik at problemet reduseres til å finne Arcsen (½).

Så det handler om å finne vinkelen hvis sinus gir ½. Den vinkelen er π/6, siden sen (π/6) = sen (30º) = ½. Derfor Arcsen (cos (π/3)) = π/6. 

Øvelser

- Oppgave 1

Finn resultatet av følgende uttrykk:

SEC (Arcan (3)) + CSC (Arccot ​​(4))

Løsning

Vi begynner å nevne α = Arcan (3) og β = Arcot (4). Så uttrykket vi må beregne er slik:

SEC (α) + CSC (β)

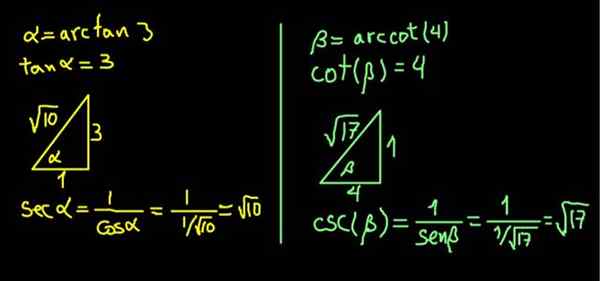
Uttrykket α = Arcan (3) tilsvarer å si det (α) = 3.

Ettersom tangenten er det motsatte benet på det tilstøtende, bygges en rektangel -trekant av kateto i motsetning til α på 3 enheter og en tilstøtende kategori på 1 enhet, slik at SO (α) = 3/1 = 3.

I et rektangel -trekant bestemmes hypotenuse av Pythagoras -teoremet. Med disse verdiene er det √10, slik at:

Sec (α) = hypotenuse / tilstøtende kateto = √10 / 1 = √10.

Tilsvarende β = Arcot (4) tilsvarer at COT (β) = 4.

En rektangel -trekant av kateto ved siden av β på 4 enheter og en motsatt kateto på 1 enhet er bygget, slik at COT (β) = 4/1.

Trekanten er umiddelbart fullført og finner sin hypotenuse takket være Pythagoras 'teorem. I dette tilfellet viste det seg å ha √17 enheter. Da beregnes CSC (β) = hypotenuse / motsatt kateto = √17 / 1 = √17.

Det kan tjene deg: y = 3sen (4x) funksjonsperiode

Husker at uttrykket vi må beregne er: 

SEC (Arcan (3)) + CSC (Arcot (4)) = Sec (α) + CSC (β) = ..

… = √10 + √17 = 3,16 + 4,12 = 7,28.

- Oppgave 2

Finn løsningene på:

Cos (2x) = 1 - sen (x)

Løsning

Det er nødvendig at alle trigonometriske funksjoner kommer til uttrykk i samme argument eller vinkel. Vi vil bruke identiteten til dobbeltvinkelen:

Cos (2x) = 1 - 2 sen²(x)

Da reduseres det opprinnelige uttrykket til:

1 - 2 sen²(x) = 1 - sin x

Når den er forenklet og faktorisert, uttrykkes det som:

sin (x) (2 sen (x) - 1) = 0

Som gir opphav til to mulige ligninger: sin (x) = 0 med løsning x = 0 og en annen ligning sen (x) = ½ med x = π/6 som en løsning.

Løsningene på ligningen som heves er: x = 0 eller x = π/6.

- Øvelse 3

Finn løsningene av følgende trigonometriske ligning:

cos (x) = synd²(x)

Løsning

For å løse denne ligningen er det praktisk å plassere en enkelt type trigonometrisk funksjon, så vi vil bruke den grunnleggende trigonometriske identiteten slik at den opprinnelige ligningen blir skrevet om som følger:

cos (x) = 1 - cos²(x)

Hvis vi navngir y = cos (x), kan uttrykket skrives om som:

og² + og - 1 = 0

Det er en andre grads ligning i og, hvis løsninger er:

y = (-1 ± √5) / 2

Da er verdiene til X som oppfyller den opprinnelige ligningen:

x = Arcos ((-1 ± √5) / 2)

Den virkelige løsningen er det positive tegnet x = 0,9046 rad = 51,83º.

Den andre løsningen er kompleks: x = (π - 1.06 i) rad.

Referanser

1. Hazewinkel, m. 1994. Encyclopaedia of Mathematics. Kluwer Academic Publisher / Springer Science & Business Media. 
2. Mobil kompis. Inverse trigonometriske funksjoner. Gjenopprettet fra: Matemovil.com
3. Universformler. Inverse trigonometriske funksjoner. Gjenopprettet fra: Universoformulas.com
4. Weisstein, Eric w. Oppfinne trigonometriske funksjoner. Gjenopprettet fra: Mathworld.Wolfram.com
5. Wikipedia. Oppfinne trigonometriske funksjoner. Hentet fra: i.Wikipedia.com