Standard estimatfeil hvor beregnet, eksempler, øvelser

Han Standard estimeringsfeil Mål avviket i en prøvepopulasjonsverdi. Det vil si at standard estimatfeil måler de mulige variasjonene av utvalget med hensyn til den sanne verdien av populasjonsgjennomsnittet.

For eksempel, hvis du vil vite gjennomsnittsalderen for befolkningen i et land (befolkningsgjennomsnitt), er det tatt en liten gruppe innbyggere, som vi vil kalle "show". Fra den er gjennomsnittsalderen (utvalgsmiddel) trukket ut og antas at befolkningen har den gjennomsnittsalderen med en standardestimatfeil som varierer mer eller mindre.

M. W. Toews [CC av 2.5 (https: // creativecommons.Org/lisenser/av/2.5)]

Det skal bemerkes at det er viktig å ikke forvirre standardavviket med standardfeilen og standardestimatfeilen:

1- Standardavviket er et mål på datadispersjon; det vil si at det er et mål på populasjonsvariabiliteten.

2- Standardfeilen er et mål på variasjonen til prøven, beregnet basert på standardavviket for befolkningen.

3- Standardestimeringsfeilen er et mål på feilen som gjøres når du tar utvalget som et estimat av populasjonsgjennomsnittet.

[TOC]

Hvordan beregnes det?

Standardestimatfeilen kan beregnes for alle tiltak oppnådd i prøvene (for eksempel standard gjennomsnittlig estimeringsfeil eller standardfeil i standardavvikestimering) og måler feilen som gjøres når du estimerer den sanne populasjonsmålet fra sin prøveverdi

Fra standardestimeringsfeilen er konfidensintervallet for det tilsvarende tiltaket bygget.

Kan tjene deg: omvendt matrise: beregning og trening løst

Den generelle strukturen til en formel for standardestimatfeilen er som følger:

Standard estimeringsfeil = ± tillitskoeffisient * Standardfeil

Tillitskoeffisient = grenseverdi for en prøvestatistikk eller prøvetakingsfordeling (normal eller Gauss Bell, Student T, blant andre) for et visst intervall av sannsynligheter.

Standardfeil = standardavvik for befolkningen delt på kvadratroten til prøvestørrelsen.

Tillitskoeffisienten indikerer mengden standardfeil som er villige til å legge til og trekke skreddersydd for å ha et visst nivå av tillit til resultatene.

Eksempler på beregning

Anta at du prøver å estimere andelen mennesker i befolkningen som har en oppførsel a, og du vil ha 95% tillit til resultatene deres.

En prøve av N -personer blir tatt, og prøveandelen P og dens komplement q bestemmes.

Standard estimeringsfeil (EEE) = ± tillitskoeffisient * Standardfeil

Stoler på koeffisient = z = 1.96.

Standardfeil = kvadratroten av årsaken mellom produktet av prøvenes andel for dets komplement og størrelsen på prøven n.

Fra standardestimatfeilen er intervallet der befolkningsandelen eller prøven andel andre prøver som kan dannes fra den befolkningen etableres, med 95% konfidensnivå:

P -ee ≤ populasjonsandel ≤ p + eee

Løste øvelser

Oppgave 1

1- Anta at du prøver å estimere andelen mennesker i befolkningen som har preferanse for en beriket meieriformel, og du vil ha 95% tillit til resultatene deres.

Kan tjene deg: syntetisk divisjon

En prøve på 800 personer blir tatt, og det er bestemt at 560 personer i utvalget har preferanse for den berikede meieriformelen. Bestem et intervall der befolkningsandelen kan forventes og andelen andre prøver som kan tas fra befolkningen, med 95% tillit

a) La oss beregne prøvenes andel P og dens komplement:

P = 560/800 = 0.70

Q = 1 -p = 1 -0.70 = 0.30

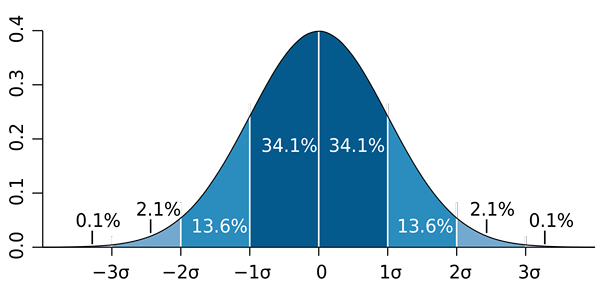
b) Det er kjent at andelen nærmer seg en normalfordeling til prøver i stor størrelse (større enn 30). Deretter blir den så -kalt regel 68 - 95 - 99 brukt.7 Og du må:

Stoler på koeffisient = z = 1.96

Standardfeil = √ (p*q/n)

Standard estimeringsfeil (EEE) = ± (1.96)*√ (0.70)*(0.30)/800) = ± 0.0318

c) Fra standardestimeringsfeilen er intervallet som befolkningsandelen forventes med 95% konfidensnivå etablert:

0.70 -0.0318 ≤ befolkningsandel ≤ 0.70 + 0.0318

0.6682 ≤ Befolkningsandel ≤ 0.7318

Du kan forvente at 70% prøveforhold vil endre opp til 3.18 prosentpoeng hvis det tar en annen prøve på 800 individer eller at den virkelige andelen av befolkningen er mellom 70 - 3.18 = 66.82% og 70 + 3.18 = 73.18%.

Oppgave 2

2- Vi tar fra Spiegel og Stephens, 2008, følgende casestudie:

Av de totale matematikkkarakterene til de første årets studenter ved et universitet, ble det tatt et tilfeldig utvalg på 50 kvalifikasjoner der gjennomsnittet var 75 poeng og standardavviket, 10 poeng. Hva er 95% konfidensgrenser for estimering av gjennomsnittet av universitetets matematikk -kvalifikasjoner?

Det kan tjene deg: Hva er forholdet mellom Rhombus -området og rektangelet?

a) La oss beregne standardestimatfeilen:

95%konfidens koeffisient = z = 1.96

Standardfeil = S/√n

Standard estimeringsfeil (EEE) = ± (1.96)*(10√50) = ± 2.7718

b) Fra standardestimatfeilen er intervallet der befolkningen gjennomsnittet eller gjennomsnittet av en annen prøve 50 er etablert, med 95% konfidensnivå:

50 -2.7718 ≤ populasjonsgjennomsnitt ≤ 50 + 2.7718

47.2282 ≤ populasjonsgjennomsnitt ≤ 52.7718

c) Du kan forvente at gjennomsnittet av prøven vil endre opp til 2.7718 poeng hvis et annet utvalg på 50 karakterer blir tatt eller at det reelle gjennomsnittet av matematikkkarakterene ved befolkningen på universitetet er mellom 47.2282 poeng og 52.7718 poeng.

Referanser

1. Abraira, v. (2002). Standardavvik og standardfeil. Smergen Magazine. Nettinnhenting.Arkiv.org.
2. Rumsey, d. (2007). Mellomstatistikk for dummies. Wiley Publishing, Inc.
3. Salinas, h. (2010). Statistikk og sannsynligheter. Gjenopprettet fra matten.Uda.Cl.
4. Sokal, r.; Rohlf, f. (2000). Biometri. Prinsippene og utøvelsen av statistikk i biologisk forskning. Tredje utg. Blume -utgaver.
5. Spiegel, m.; Stephens, l. (2008). Statistikk. Fjerde utg. McGraw-Hill/Inter-American fra Mexico S. TIL.
6. Wikipedia. (2019). 68-95-99.7 Regel. Innhentet fra.Wikipedia.org.
7. Wikipedia. (2019). Standard feil. Innhentet fra.Wikipedia.org.