Prosentvis feil
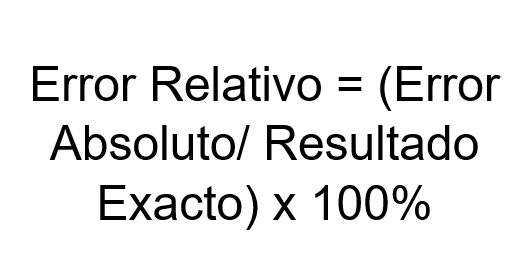
- 1596
- 281
- Prof. Oskar Aas
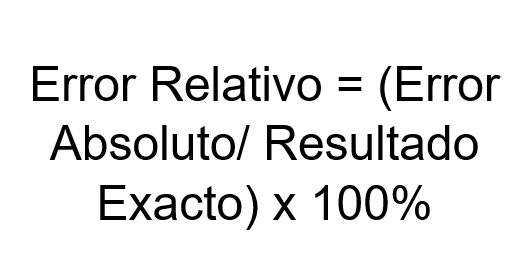
Hva er prosentvis feil?
Han Prosentvis feil Det er manifestasjonen av en relativ feil i prosentvis vilkår. Med andre ord, det er en numerisk feil uttrykt av verdien som gir en relativ feil, deretter multiplisert med 100.
For å forstå hva en prosentvis feil er, må du først forstå hva en numerisk feil, en absolutt feil og en relativ feil, siden prosentvis feil er avledet fra disse to begrepene.
En numerisk feil er en som vises når et tiltak blir tatt tvetydig når du bruker en enhet (direkte måling), eller når en matematisk formel (indirekte tiltak) brukes dårlig.
Alle numeriske feil kan uttrykkes absolutt eller prosentvis. For sin del er den absolutte feilen en som oppstår når du utfører en tilnærming for å representere en matematisk mengde som følge av måling av et element eller feilaktig anvendelse av en formel.
På denne måten endres den eksakte matematiske verdien av tilnærmingen. Beregningen av den absolutte feilen gjøres ved å trekke fra tilnærmingen til den eksakte matematiske verdien, som denne:
Absolutt feil = eksakt resultat - tilnærming
Målenhetene som brukes til å manifestere den relative feilen er de samme som brukes til å snakke om den numeriske feilen. Tilsvarende kan denne feilen gi en positiv eller negativ verdi.
Den relative feilen er kvotienten oppnådd ved å dele den absolutte feilen med den eksakte matematiske verdien.
På denne måten er den prosentvise feilen det som oppnås ved å multiplisere resultatet av den relative feilen per 100. Med andre ord, prosentvis feil er prosentandelen (%) uttrykk for den relative feilen.
Kan tjene deg: x kvadratRelativ feil = (absolutt feil/ eksakt resultat)
En prosentvis verdi som kan være negativ eller positiv, det vil si at det kan være en verdi representert av overskudd eller standard. Denne verdien, i motsetning til den absolutte feilen, presenterer ikke enheter utover prosentandelen (%).
Relativ feil = (absolutt feil/ eksakt resultat) x 100%
Oppdraget med relative og prosentvise feil er å indikere kvaliteten på noe, eller gi komparativ verdi.
Eksempler på beregning av prosentvis feil
1. To -landmåling
Ved å måle to partier eller land, sies det at det er omtrent 1 m feil i målingen. Et land er 300 meter og en annen av 2.000.
I dette tilfellet vil den relative feilen for den første målingen være større enn den andre, siden i proporsjon 1 m representerer en høyere prosentandel.
300 m parti:
EP = (1/300) x 100%
EP = 0,33%
Mye av 2.000 m:
EP = (1/2.000) x 100%
EP = 0,05%
2. Måling av aluminium
I et laboratorium leveres en aluminiumsblokk. Når du måler dimensjonene til blokken og beregner dens masse og volum, bestemmes dens tetthet (2,68 g/cm³).
Når du sjekker den numeriske tabellen til materialet, indikerer dette imidlertid at aluminiumtettheten er 2,7 g/cm³. På denne måten vil den absolutte og prosentvise feilen bli beregnet som følger:
EA = 2,7 - 2,68
EA = 0,02 g/cm³.
EP = (0,02/2,7) x 100%
EP = 0,74%
3- Delta på et arrangement
Det ble antatt at 1.000.000 mennesker ville gå til en viss begivenhet. Imidlertid var det nøyaktige antallet personer som gikk til dette arrangementet 88.000. Den absolutte og prosentvise feilen ville være følgende:
Kan tjene deg: tilfeldig variabel: konsept, typer, eksemplerEa = 1.000.000 - 88.000
EA = 912.000
EP = (912 000/1.000.000) x 100%
EP = 91,2%
4. Ball Fall
Tiden som er beregnet må ta en ball for å nå bakken etter å ha blitt kastet i en avstand på 4 meter er 3 sekunder.
På eksperimenteringstidspunktet oppdages det imidlertid at ballen tok 2,1 sekunder å nå bakken.
EA = 3 - 2.1
EA = 0,9 sekunder
EP = (0,9/2,1) x 100%
EP = 42,8%
5. Det tar en bil å ankomme
Det anslås at hvis en bil går på 60 km, vil den nå sin destinasjon om 1 time. Imidlertid tok bilen i det virkelige liv 1,2 timer å nå sin destinasjon. Den prosentvise feilen i denne tidsberegningen vil bli uttrykt som følger:
EA = 1 - 1.2
EA = -0.2
EP = (-0.2/1.2) x 100%
EP = -16%
6. Målingslengde
Enhver lengde måles med en verdi på 30 cm. Å verifisere måling av denne lengden er tydelig at det var en feil på 0,2 cm. Prosentfeilen i dette tilfellet vil bli manifestert som følger:
EP = (0,2/30) x 100%
EP = 0,67%
7. Brolengde
Beregningen av lengden på en bro i henhold til planene er 100 m. Når du bekrefter denne lengden, når den er bygget, er det imidlertid tydelig at den faktisk er 99,8 m lang. Prosentvis feil vil bli bevist på denne måten.
EA = 100 - 99.8
Ea = 0,2 m
EP = (0,2/99,8) x 100
EP = 0,2%
8. Diameteren på en skrue
Hodet til en standard produsert skrue er 1 cm i diameter.
Kan tjene deg: kontinuerlig ensartet distribusjon: egenskaper, eksempler, applikasjonerNår du måler denne diameteren, observeres det imidlertid at skruehodet virkelig har 0.85 cm. Prosentvis feil vil være som følger:
EA = 1 - 0,85
EA = 0,15 cm
EP = (0,15/0,85) x 100
EP = 17,64%
9. Objektvekt
I henhold til volumet og materialene anslås det at vekten til et gitt objekt er 30 kilo. Når objektet er analysert, observeres det at dens virkelige vekt er 32 kilo.
I dette tilfellet blir verdien av prosentvis feil beskrevet som følger:
EA = 30 - 32
Ea = -2 kilo
EP = (2/32) x 100
EP = 6,25%
10. Stålmåling
I et laboratorium studeres et stålark. Når du måler dimensjonene på arket og beregner dets masse og volum, bestemmes tettheten av det samme (3,51 g/cm³).
Når du sjekker den numeriske tabellen til materialet, indikerer dette imidlertid at tettheten til stålet er 2,85 g/cm³. På denne måten vil den absolutte og prosentvise feilen bli beregnet som følger:
EA = 3,51 - 2,85
EA = 0,66 g/cm³.
EP = (0,66/2,85) x 100%
EP = 23,15%
Referanser
- Prosentvis feil. Gjenopprettet fra matematikk.com
- Hvordan beregne prosentfeil. Gjenopprettet fra Thoughtco.com

