Estimering etter intervaller

Hva er estimering etter intervaller?

De Estimering etter intervaller Det er måten å bestemme verdiene som befolkningsgjennomsnittet kan inkluderes, basert på informasjonen til et utvalg av endelig størrelse, tilfeldig utvunnet fra den totale befolkningen.

Han Estimeringsintervall Den er lavere ettersom prøven er større, men den blir bredere hvis nivået eller prosentandelen av påliteligheten av de samme øker.

Hvis du ønsker å kjenne befolkningsgjennomsnittet av en viss variabel i nøyaktig form, bør den totale befolkningen vurderes, noe som ikke alltid er mulig, siden hvis det er en veldig stor befolkning, er det dyrt å få dataene til hele befolkningen. Av denne grunn brukes en eller flere tilfeldige prøver av den totale befolkningen å ta.

Det er basert på hypotesen at ved å trekke ut en tilfeldig prøve, ikke partisk og ta hensyn til proporsjonalt alle lag, må gjennomsnittsverdien til prøven være veldig nær den for befolkningsgjennomsnittet.

Logikken indikerer at jo større prøvedata, forskjellen mellom den gjennomsnittlige prøveverdien og den gjennomsnittlige populasjonsverdien er lavere.

Estimeringsintervall

I praksis, med mindre den komplette befolkningen er kjent, er det bare mulig å finne, med en viss sannsynlighet, intervallet der befolkningen betyr, basert på et utvalg av endelig størrelse.

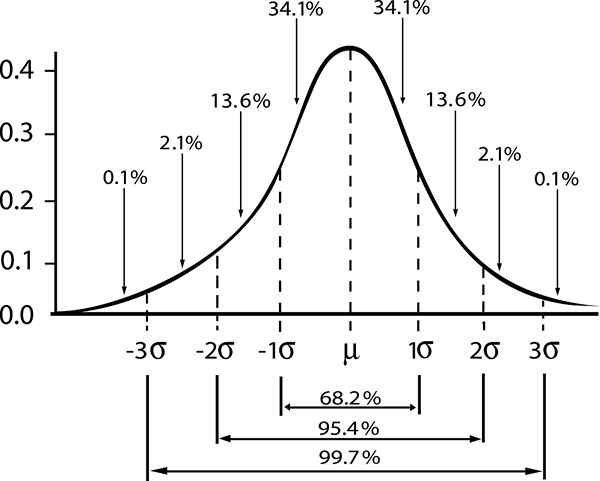
I tilfelle av en befolkning som følger en normalfordeling, med Standardavvik σ , de Standard forskjell Mellom befolkningsgjennomsnittet μ og den gjennomsnittlige prøven av størrelse n er gitt av:

| μ - | ≤ σ / √n

Her indikerer ordet "standard" at 68% av størrelsesprøver n, De har gjennomsnittsverdi mellom intervallet [μ - σ / √n, μ + σ / √n].

Kan tjene deg: delbarhetskriterier: Hva er de, hva er bruk og regler

Standardestimat

En alternativ tolkning av ovennevnte vil være å si at befolkningen oppnådd fra et utvalg av størrelse n og gjennomsnittsverdien forstås i intervallet  [ - σ / √n, + σ / √n], Med 68% sannsynlighet.

I de fleste virkelige tilfeller er det ikke mulig å kjenne standardbefolkningsavviket, så σ Det er tilnærmet med standardavviket til prøven s, som beregnes som følger:

S = √ (∑ (x_Yo - )² / √ (n-1).

Derfra får du intervallet som kan inneholde befolkningsgjennomsnittet med et 68% konfidensnivå (standard konfidensnivå), gitt av:

  -s / √n ≤ μ ≤ + s / √n

Dette populasjonsmålingsintervallet er kjent som standardestimeringsintervall og ble bare innhentet med de tilgjengelige dataene i størrelse n.

Fra forrige formel følger det at hvis du ønsket å styrke estimeringsintervallet i to, er det nødvendig firedoblet Størrelsen på prøven.

Estimering etter konfidensintervaller

I visse studier kan et standardnivå på 68% være utilstrekkelig, da er det nødvendig å bestemme intervallene med et vilkårlig konfidensnivå γ.

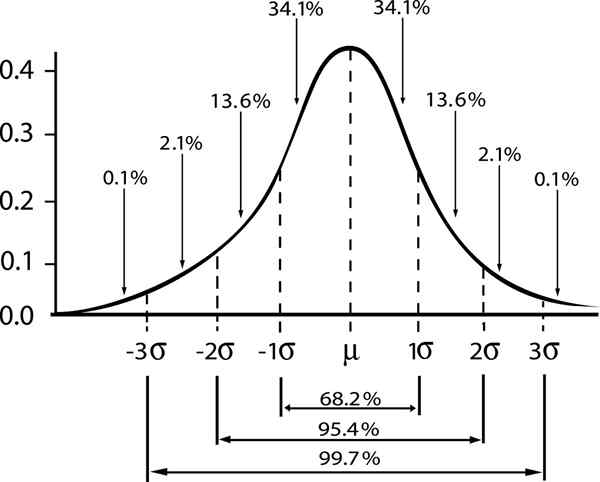Forholdet mellom pålitelighetsmarginen og intervallet i en Gaussisk distribusjon vises

Hvis vi betegner av ε Standardfeilen s/√n, da estimeringsfeilen for et konfidensnivå γ vil bli gitt av:

E = Zy⋅ε.

Hvor Zy Det er et tall som standardfeilen multipliseres, og dermed oppnå feilmarginen med et vilkårlig konfidensnivå γ.

For å få faktoren Zy, fortsett som følger:

Det kan tjene deg: rasjonelle tall: egenskaper, eksempler og operasjoner

Trinn 1

Er samtalen nivå av betydning α Tilsvarende nivået av tillit γ etter følgende formel:

α = 1 - γ

Steg 2

Verdien bestemmes:

Dette er den akkumulerte frekvensen i en normalfordeling som er karakterisert N (0,1) I intervallet (-∞, Zy ].

Trinn 3

Det rydder Zy Ligningen:

N (zγ) = 1 - α/2

Siden det er en integrert ligning, oppnås denne klaring fra normalfordelingstabellene ved bruk av den lineære interpolasjonsmetoden.

Trinn 4

Alternativt til bruk av tabeller, innlemmet de statistiske funksjonene i regnearkene som for eksempel utmerke, enten Google ark. Disse programmene inneholder normal inverse funksjon N^-1, slik at korreksjonsfaktoren Zy Det oppnås direkte å evaluere denne omvendte funksjonen:

Zy = n^-1(1 - α/2).

Typiske tillitsintervaller

De mest brukte konfidensnivåene er:

• Zy = 1; Standard konfidensnivå γ = 0,68.
• Zy = 2; selvtillitsnivå γ = 0,95 (eller nivå av betydning 5%).
• Zy = 3; selvtillitsnivå γ = 0,997 (eller 0,3%nivå av betydning)

Eksempler

Eksempel 1

Bestem det gjennomsnittlige vektintervallet for nyfødte i løpet av august måned i en stor by basert på en tilfeldig prøve på 100 babyer, der en gjennomsnittlig vekt på 3100 gram ble oppnådd med en prøvestandardavvik s = 1500 gram.

Løsning

For det første bestemmes standardfeilen til prøven:

ε = s/√n = (1500 g)/√100 = 150 g.

Derfor, med utgangspunkt i denne prøven, kan det utledes at gjennomsnittsvekten av babyer født i august i den byen er mellom 2950 g og 3250 g, med 68% sannsynlighet.

Eksempel 2

Anta at størrelsen på utvalget av babyer født i samme måned i august og i samme by med eksempel 1. Den gjennomsnittlige prøvevekten er 3100 g med en standard 1500 g spredning. 

Det kan tjene deg: nedbrytning av naturlige tall (eksempler og øvelser)

Det blir bedt om å estimere gjennomsnittlig vektintervall for de nyfødte i den byen, fra denne nye prøven.

Løsning

Nå synker standardfeilen i faktor 1/√2, Så den nye standardfeilen i gjennomsnittsvekten vil være 106 g.

Deretter kan det estimeres, fra denne nye prøven at den gjennomsnittlige vekten av nyfødte består i området 2994 g til 3206 g, med 68% sannsynlighet.

Øvelser

Oppgave 1

Bestem det gjennomsnittlige vektområdet for nyfødte i august, med start fra utvalget som er spesifisert i eksempel 1, med 95% sannsynlighet.

Løsning

Et 95% pålitelighetsnivå dobler det gjennomsnittlige vektområdet, sammenlignet med et 68% pålitelighetsnivå.

Derfor er gjennomsnittsvekten til nyfødte inkludert i området 2800 gram på 3400 gram med 95% sikkerhet.

Oppgave 2

Estimere med et 99,7% konfidensnivå Intervallet der gjennomsnittsvekten til nyfødte fra en stor by vil bli funnet, hvis en prøve er tilgjengelig med gjennomsnittsvekten på 100 babyer som tilsvarer 3100 g, og med et standard prøveavvik s = 1500 g.

Løsning

Gjennomsnittlig vektfeilmargin, med 99,7% av sikkerheten, vil være tredoblet den gjennomsnittlige feilen, det vil si:

3*1500/√100.

Deretter utledes det fra denne prøven at gjennomsnittsvekten de nyfødte vil bli inkludert i intervallet: 2650 gram til 3550 gram, med et sikkerhetsnivå på 99,7%. 

Fra dette resultatet blir det observert som med et større nivå av sikkerhet øker usikkerheten om gjennomsnittsvekten til et mye bredere intervall.