Normal innsats hva det består av, hvordan det beregnes, eksempler

Han normal innsats Brukes på et visst materiale, også kalt uniaxial innsats, er det forholdet mellom den anvendte kraften vinkelrett på en viss overflate og det krysseseksjonsområdet som den virker på, eller belastningen per enhet av areal. Matematisk, hvis P er størrelsen på kraften og A er området der det brukes, er innsatsen σ kvotienten: σ = p/a.

Enhetene for normal innsats i det internasjonale systemet er Newton /Metro², kjent som Pascal og forkortet PA. Dette er de samme trykkenhetene. Andre enheter som vises i litteraturen er ofte kilo / tomme² enten psi.

Figur 1. Bergarter blir stadig utsatt for innsats på grunn av tektonisk aktivitet, noe som forårsaker deformasjoner i jordskorpen. Kilde: Pixabay.

I figur 2 påføres to krefter i like stor størrelsesorden vinkelrett på det kors -spiselige området, noe som gjør en trekkraft på selve lysstangen som har en tendens til å utvide den.

Disse kreftene gir en normal innsats som også kalles Aksial belastning sentrert, fordi dens handlingslinje sammenfaller med den aksiale aksen, som centroid ligger.

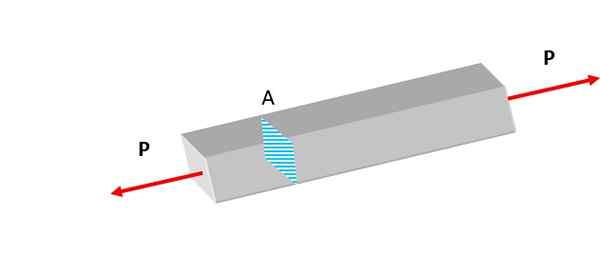Figur 2. Den viste linjen er underlagt trekkraft. Kilde: Selvlaget.

Innsats, enten det er normale eller andre typer, vises kontinuerlig i naturen. I litosfæren er bergartene utsatt for tyngdekraft og tektonisk aktivitet, og eksperimenterer deformasjoner.

På denne måten har strukturer som bretter og feil opprinnelse, hvis studie er viktig i bruken av mineraler og sivilingeniør, for bygging av bygninger og veier, for å nevne noen eksempler.

[TOC]

Hvordan beregnes det?

Ligningen gitt i begynnelsen σ = p/a gjør det mulig å beregne den gjennomsnittlige normale innsatsen på det aktuelle området. Verdien av P er størrelsen på den resulterende kraften over området som brukes på centroid og er tilstrekkelig for mange enkle situasjoner.

I dette tilfellet er fordelingen av krefter ensartet, spesielt på punkter bort fra der du har stangen underlagt trekkraft eller komprimering. Men hvis innsatsen er nødvendig for å beregne på et bestemt punkt eller kreftene ikke blir fordelt jevnt, er det nødvendig å bruke følgende definisjon:

Kan tjene deg: lukket elektrisk krets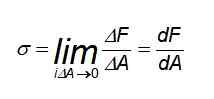

Generelt sett kan verdien av innsatsen på et bestemt punkt være forskjellig fra gjennomsnittsverdien. Faktisk kan innsatsen variere i henhold til seksjonen å vurdere.

Dette er illustrert i den følgende figuren, der trekkreftene F prøver å skille linjen i likevekt i seksjonene mm og nn.

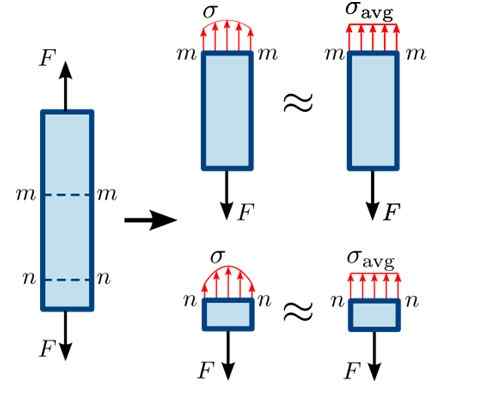Figur 3. Distribusjon av normal innsats i forskjellige deler av en stolpe. Kilde: https: // Commons.Wikimedia.org/wiki/fil: normal_stress.Svg#/media/fil: normal_stress.Svg

Som seksjonen nn Det er veldig nær der kraft F ned, fordelingen av krefter på overflaten er ikke helt homogen, disse mindreårige er jo lenger det er fra det punktet. Distribusjonen er litt mer homogen i seksjonen mm.

I alle fall har den normale innsatsen alltid en tendens til å strekke seg eller komprimere de to delene av kroppen som finnes på begge sider av flyet de virker. På den annen side har andre forskjellige anstrengelser, for eksempel skjær, en tendens til å bevege seg og skille disse delene.

Hooke's lov og normal innsats

Hooke's lov uttaler at innen elastiske grenser er den normale innsatsen direkte proporsjonal med deformasjonen som baren eller objektet opplever. I så fall:

Normal innsats ∝ Unitary Deformation

Proporsjonalitetskonstanten er den unge (y) modulen:

Normal innsats (σ) = Young Module (Y) x Unitary Deformation (ε)

σ = y. ε

Med ε = ΔL/L, hvor ΔL er forskjellen mellom finalen og den første lengden, som er l.

Den unge modulen eller elastisitetsmodulen er et kjennetegn ved materialet, hvis dimensjoner er de samme som for innsatsen, siden enhetsdeformasjonen er dimensjonsløs.

Det kan tjene deg: 13 eksempler på Newtons andre lov i hverdagen

Viktigheten av innsats i motstanden mellom materialer og geologi

Å bestemme hvor motstandsdyktig er materialene til innsats er veldig viktig. For strukturer som brukes i bygging av bygninger, så vel som i utformingen av deler for forskjellige enheter, er det nødvendig å sikre at materialene som er valgt på riktig måte oppfylle sin funksjon.

Derfor analyseres materialer uttømmende i laboratorier gjennom forsøk som er bestemt til å vite hvor mye kraft de kan motstå før de deformeres og bryter, og dermed mister funksjonene sine. Basert på dette tas avgjørelsen om å produsere et bestemt stykke eller være en del av en enhet eller ikke.

Det antas at den første forskeren systematisk studerte motstanden til materialene var Leonardo da Vinci. Han etterlot bevis på forsøk der han bestemte motstanden til ledninger som henger steiner av forskjellige pesos.

I krefter er både omfanget av styrken og også dimensjonene til strukturen og hvordan den brukes viktig, for å etablere grensene som materialet har en elastisk oppførsel; det vil si at den går tilbake til sin opprinnelige form når innsatsen opphører.

Med resultatene av disse testene utføres innsatsdeformasjonskurver for forskjellige typer materialer, for eksempel stål, betong, aluminium og mange flere.

Eksempler

I de følgende eksempler antas det at kreftene er fordelt jevnt, og at materialet er homogent og isotropisk. Dette betyr at egenskapene er de samme i alle retninger. Derfor er det gyldig å anvende ligningen σ = p/a for å finne innsats.

-Oppgave 1

I figur 3 er det kjent at den gjennomsnittlige normale innsatsen som virker på AB -seksjonen har størrelsesorden 48 kPa. Finn: a) Størrelsen på kraften f som virker i CB, b) Innsatsen på seksjon BC.

Det kan tjene deg: Horisontal skyting: Kjennetegn, formler og ligninger, øvelser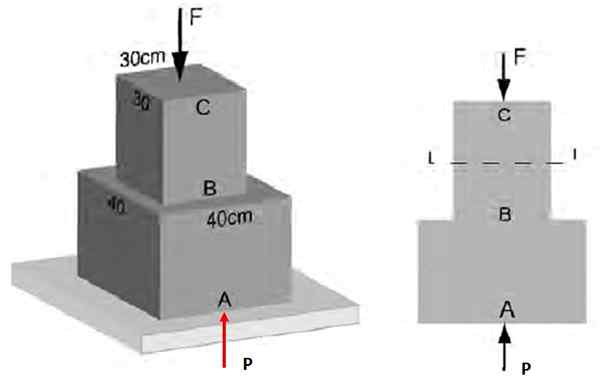Figur 4. Normal innsats på strukturen i eksempel 1 ..

Løsning

Siden strukturen er i statisk likevekt, i henhold til Newtons andre lov:

P-F = 0

Den normale innsatsen på AB -seksjonen har størrelse:

σ_AB = P/a_AB

Hvor p = σ_AB . TIL_AB = 48000 pa. (40 x 10 ^-2 m)² = 7680 n

Derfor f = 7680 n

Den normale innsatsen på seksjon BC er forholdet mellom størrelsen på F og området av tverrsnittet på den siden:

σ_BC = F/a_BC = 7680 n / (30 x 10 ^-2 m)² = 85.3 kPa.

-Oppgave 2

En 150 m ledning lang og 2.5 mm i diameter er strukket av en 500 N -kraft. Finne:

a) langsgående innsats σ.

b) enhetlig deformasjon, vel vitende om at den endelige lengden er 150.125 m.

c) Elastisitetsmodulen OG av denne ledningen.

Løsning

a) σ = f / a = f / π.r²

Ledningens radius er halvparten av diameteren:

R = 1.25 mm = 1.25 x 10^-3 m.

Kors -avsnittsarealet er π.r², Da er innsatsen:

σ = f / π.r² = 500 / (π.(1.25 x 10^-3)² PA = 101859.2 Pa

b) ε = ΔL / l = (sluttlengde - startlengde) / startlengde

Derfor:

ε = (150.125 - 150) /150 = 0.125/150 = 0.000833

c) Youngs modul av ledningen blir fjernet ved å kjenne verdiene til ε og σ tidligere beregnet:

Y = σ / ε = 101859.2 PA / 0.000833 = 1.22 x 10⁸ PA = 122 MPa.

Referanser

1. Øl, f. 2010. Materialmekanikk. 5. plass. Utgave. McGraw Hill. 7 - 9.
2. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6^tth  Ed. Prentice Hall. 238-242.
3. Hibbeler, R.C. 2006. Materialmekanikk. 6. Utgave. Pearson Education. 22 -25
4. Valera Negrete, J. 2005. Generelle fysikknotater. Unam. 87-98.
5. Wikipedia. Stress (mekanikk). Gjenopprettet fra: Wikipedia.org.