Base og dimensjonsvektorrom, aksiomer, egenskaper

EN vektorrom Det er et ikke -fritid sett V= eller, v, W,…, hvis elementer er vektorer. Med seg utføres noen viktige operasjoner, blant dem følgende skiller seg ut:

- Sum mellom to vektorer u + v som et resultat z, som tilhører helheten V.

- Multiplikasjon av et reelt tall α med en vektor v: α v Det gir en annen vektor og som tilhører V.

Kunstnerisk visjon av et vektorrom. Kilde: Pixabay

For å betegne en vektor bruker vi fet skrift (v Det er en vektor), og for skalarene eller tallene greske bokstaver (α er et tall).

[TOC]

Aksiomer og egenskaper

For å være et vektorrom, må de neste åtte aksiomene oppfylles:

1-konmutabilitet: eller +v = v +eller

2-transitivitet: (eller + v) + W = eller + ( v + W)

3-eksistens av nullvektoren 0 slik at 0 + v = v

4-eksistens av det motsatte: det motsatte av v er (-v) , gitt at v + (-v) = 0

5-produktdistributivitet med hensyn til vektorsummen: α ( eller + v ) = αeller +αv

6-produktdistributivitet med hensyn til den skalære summen: (α + β)v = αv +βv

7-assosiativitet av skalarproduktet: α (β v) = (α β)v

8-tallet 1 Det er det nøytrale elementet siden: 1v = v

Eksempler på vektorrom

Eksempel 1

Vektorer i planet (R²) er et eksempel på vektorrom. En vektor i planet er et geometrisk objekt som har størrelse og retning. Det er representert av et orientert segment som tilhører nevnte plan og med en størrelse proporsjonal med dets størrelsesorden.

Summen av to vektorer i planet kan defineres som den geometriske driften av den andre vektoren etter den første. Resultatet av summen er det orienterte segmentet som starter fra opprinnelsen til den første og når spissen av sekundet.

I figuren kan det bemerkes at summen i R² er kommutativ.

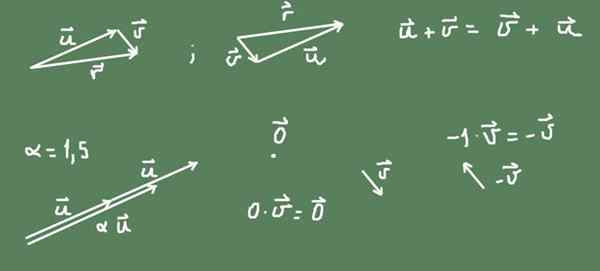Figur 2. Vektorer i planet danner vektorrom. Kilde: Selvlaget.

Produktet av et α -tall er også definert av en vektor. Hvis tallet er positivt, opprettholdes den opprinnelige vektoradressen og størrelsen er α ganger den opprinnelige vektoren. Hvis tallet er negativt, er adressen motsatt, og den resulterende vektorstørrelsen er den absolutte verdien av tallet.

Vektoren i motsetning til en vektor noen v er -v = (-1) v.

Nullvektoren er et punkt i R² -planet, og nulltallet med en vektor resulterer i nullvektoren.

Alt sagt er illustrert i figur 2.

Eksempel 2

Sett P Av alle polynomer mindre enn eller lik to, inkludert nullkarakteren, danner de et sett som oppfyller alle aksiomene i et vektorrom.

Det kan tjene deg: gjensidig utelukkende hendelser: egenskaper og eksempler

Være polynomet p (x) = a x² + b x + c y q (x) = d x² + e x + f

Summen av to polynomer er definert: p (x) + q (x) = (a + d) x² + (b + e) ​​x + (c + f)

Summen av polynomer som tilhører helheten P Det er kommutativ og transitive.

Nullpolynomet som tilhører helheten P Det er en som har alle sine koeffisienter lik null:

0 (x) = 0 x² + 0 x + 0

Summen av en α -skalar er definert av en polynom som: α P (x) = α ∙ A x² + α ∙ B x + α ∙ C

Det motsatte polynomet av p (x) er -p (x) = (-1) P (x).

Fra alt dette følger det at settet P Av alle polynomer mindre enn eller lik to, er det et vektorrom.

Eksempel 3

Sett M av alle matriser med m rader x n kolonner hvis elementer er reelle tall danner et reelt vektorrom, med hensyn til summen av matriser og produkt av et tall med en matrise.

Eksempel 4

Settet F for kontinuerlige funksjoner av reell variabel, danner et vektorrom, siden summen av to funksjoner kan defineres, multiplikasjonen av en skalar med en funksjon, nullfunksjonen og den symmetriske funksjonen. De oppfyller også aksiomene som kjennetegner et vektorrom.

Base og dimensjon av et vektorrom

Utgangspunkt

Et sett med lineært uavhengige vektorer er definert som grunnlaget for et vektorrom slik at fra en lineær kombinasjon av dem kan en vektor av det vektorrommet genereres.

Lineært å kombinere to eller flere vektorer består i å multiplisere vektorer med noen skalar og deretter legge dem vektorly.

For eksempel, i vektorområdet til vektor i tre dimensjoner dannet av R³, brukes den kanoniske basen definert av enhetsvektorene (av størrelsesorden 1) (av størrelsesorden 1) Yo, J, k.

Hvor Yo = (1, 0, 0); J = (0, 1, 0); k = (0, 0, 1). Dette er kartesiske eller kanoniske vektorer.

Hvilken som helst vektor V tilhører r³ er skrevet som V = a Yo + b J + c k, som er en lineær kombinasjon av basevektorer Yo, J, k. Skalarer eller tall A, B, C er kjent som kartesiske komponenter av V.

Det sies også at grunnvektorene til et vektorrom danner et sett med vektorrom.

Dimensjon

Dimensjonen til et vektorrom er kardinalnummeret til en vektorbase for nevnte rom; det vil si antall vektorer som utgjør nevnte base.

Denne kardinal er det maksimale antall lineært uavhengige vektorer av det vektorrommet, og samtidig minimum antall vektorer som danner et generasjonssett med nevnte rom.

Kan tjene deg: Statistisk populasjon: konsept, typer, eksempler

Basene på et vektorrom er ikke unike, men alle basene på samme vektorrom har samme dimensjon.

Vektor underområde

Et vektor underområde av et vektorrom v er et undergruppe av V der de samme operasjonene er definert som i V og oppfyller alle aksiomene til vektorrommet. Derfor vil underområdet også være et vektorrom.

Eksempel på vektorunderlag er vektorene som tilhører XY -planet. Dette underområdet er et undergruppe av et vektorrom med dimensjonalitet større enn settet med vektorer som tilhører det tre -dimensjonale rommet xyz.

Et annet eksempel på vektorunderlaget S1 i vektorrommet er dannet av alle 2 × 2 matriser med ekte elementer er det som er definert nedenfor:

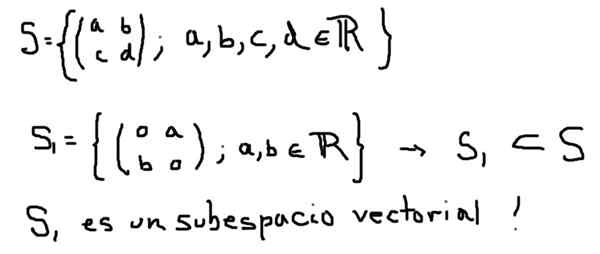
På den annen side, S2 definert nedenfor, selv om det er en delmengde av S, danner den ikke et vektorunderlag:

Løste øvelser

-Oppgave 1

Være vektorene V1= (1, 1, 0); V2= (0, 2, 1) og V3= (0, 0, 3) i R³.

a) Bevis at de er lineært uavhengige.

b) Bevis at de danner en base i R³, siden enhver liste (x, y, z) kan skrives som en lineær kombinasjon av V1, V2, V3.

c) Finn komponentene på listen V = (-3,5,4) ved basen V1, V2, V3.

Løsning

Kriteriet for å demonstrere lineær uavhengighet er å etablere følgende sett med ligninger i α, β og γ

α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)

I tilfelle den eneste løsningen på dette systemet er α = β = γ = 0, er vektorene lineært uavhengige, ellers er de ikke.

For å oppnå verdiene til α, β og γ foreslår vi følgende ligningssystem:

α ∙ 1 + β ∙ 0 + γ ∙ 0 = 0

α ∙ 1 + β ∙ 2 + γ ∙ 0 = 0

α ∙ 0 + β ∙ 1 + γ ∙ 3 = 0

Den første fører til α = 0, den andre α = -2 ∙ β, men som α = 0 da β = 0. Den tredje ligningen innebærer at γ = (-1/3) β, men som β = 0 da γ = 0.

Svar til

Det konkluderes med at det er et sett med lineært uavhengige vektorer i R³ .

Svar b

La oss nå skrive listen (x, y, z) som en lineær kombinasjon av V1, V2, V3.

(x, y, z) = α v1 + β v2 + γ v3 = α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)

α ∙ 1 + β ∙ 0 + γ ∙ 0 = x

α ∙ 1 + β ∙ 2 + γ ∙ 0 = y

Det kan tjene deg: Tukey Test: Det som er i tilfelle av eksempel løst trening

α ∙ 0 + β ∙ 1 + γ ∙ 3 = z

Hvor du har:

α = x

α + 2 β = y

β + 3 γ = z

Den første indikerer α = x, den andre β = (y-x)/2 og den tredje γ = (z- y/2 +x/2)/3. På denne måten har vi funnet generatorene av α, β og γ på hvilken som helst R³ -liste 

Svar c

La oss finne komponentene på listen V = (-3,5,4) ved basen V1, V2, V3.

Vi erstatter de tilsvarende verdiene i uttrykkene som er funnet ovenfor for generatorene.

I dette tilfellet har vi: α = -3; β = (5-(-3))/2 = 4; γ = (4- 5/2 +(- 3)/2)/3 = 0

Det er:

(-3,5,4) = -3 (1, 1, 0) + 4 (0, 2, 1) + 0 (0, 0, 3)

Endelig:

V = -3 V1 + 4 V2 + 0 V3

Vi konkluderer med det V1, v2, v3 De danner en base i vektorrommet r³ av dimensjon 3.

-Oppgave 2

Express Polynomial P (T) = T² + 4T -3 som en lineær kombinasjon av P1 (T) = T² -2t + 5, P2 (T) = 2T² -3T og P3 (T) = T + 3.

Løsning

P (t) = x P1 (t) + og p2 (t) + z p3 (t)

der tallene x, y, z må bestemmes.

Ved å multiplisere og gruppere vilkår med samme grad i t oppnås det:

T² + 4 t -3 = (x + 2y) t² + (-2x -3y + z) t + (5x + 3z)

Som fører oss til følgende ligningssystem:

x + 2y = 1

-2x -3y + z = 4

5x + 3z = -3

Løsningene av dette ligningssystemet er:

x = -3, y = 2, z = 4.

Det er:

P (T) = -3 P1 (T) + 2 P2 (T) + 4 P3 (T)

-Øvelse 3

Vis at vektorer V1= (1, 0, -1, 2); V2= (1, 1, 0, 1) og V3= (2, 1, -1, 1) av R⁴ er lineært uavhengige.

Løsning

Vi kombinerer lineært de tre vektorene V1, V2, V3 Og vi krever at kombinasjonen legger til nullelementet til R⁴

til V1 + b V2 + c V3 = 0

Det er å si,

A (1, 0, -1, 2) + B (1, 1, 0, 1) + C (2, 1, -1, 1) = (0, 0, 0, 0)

Dette fører oss til følgende ligningssystem:

A + b + 2 c = 0

B + C = 0

-A - C = 0

2 a + b + c = 0

Trekk fra den første og fjerde vi har: -A + C = 0 Det som innebærer A = C.

Men hvis vi ser på den tredje ligningen, må vi = -c. Den eneste måten å møte a = c = (-c) er at C er 0 og derfor vil også være 0.

A = c = 0

Hvis vi erstatter dette resultatet i den første ligningen, konkluderer vi at b = 0.

Endelig a = b = c = 0, så det kan konkluderes at vektorer v1, v2 og v3 er lineært uavhengige.

Referanser

1. Lipschutz, s. 1993. Lineær algebra. Andre utgave. McGraw - Hill. 167 - 198.