Tilfeldig eksperimentkonsept, prøveområde, eksempler

Det er snakk om Tilfeldig eksperiment Når resultatet av hver enkelt prøve er uforutsigbar, selv når sannsynligheten for forekomst av et visst resultat kan etableres.

Imidlertid bør det avklares at det ikke er mulig å reprodusere det samme resultatet av et tilfeldig system med de samme innledende parametrene og forholdene i hver prøve av eksperimentet.

Figur 1. Terninglansering er et tilfeldig eksperiment. Kilde: Pixabay.

Et godt eksempel på et tilfeldig eksperiment er lanseringen av en terning. Selv når du passer på å lansere terningen på samme måte, vil det oppnås et uforutsigbart resultat i hvert forsøk. Det eneste som kan bekreftes er faktisk at resultatet kan være noe av følgende: 1, 2, 3, 4, 5 eller 6.

Lanseringen av en valuta er et annet eksempel på tilfeldig eksperiment med bare to mulige resultater: ansikt eller forsegling. Selv om valutaen er lansert fra samme høyde og på samme måte, vil sjansefaktoren alltid være til stede, noe som resulterer i usikkerhet til hvert nytt forsøk.

Det motsatte av et tilfeldig eksperiment er et deterministisk eksperiment. For eksempel er det kjent at hver gang vann kokes ved havnivået er koketemperaturen 100 ºC. Men det hender aldri at resultatet er noen ganger 90 ºC, ytterligere 12 0 ºC og noen ganger 100 ºC.

[TOC]

Prøveområde

Settet med alle mulige resultater av et tilfeldig eksperiment kalles prøveområde. I det tilfeldige eksperimentet med lanseringen av en terninger er prøveområdet:

D = 1, 2, 3, 4, 5, 6.

På sin side, ved lanseringen av en valuta, er utvalgsområdet:

M = ansikt, forsegling.

Arrangement eller arrangement

I et tilfeldig eksperiment, a begivenhet Det er forekomsten eller ikke av et visst resultat. For eksempel, i tilfelle av lanseringen av en valuta, er en hendelse eller en begivenhet å være dyr.

Kan tjene deg: homologe sider

En annen hendelse i et tilfeldig eksperiment kan være som følger: at ved lanseringen av en terning er et tall mindre enn tre utgitt.

I tilfelle hendelsen finner sted, er settet med mulige resultater settet:

E = 1, 2, 3

I sin tur er dette en delmengde av plassen eller prøvesettet:

M = 1, 2, 3, 4, 5, 6.

Eksempler

Nedenfor er noen eksempler som illustrerer det ovennevnte:

Eksempel 1

Anta at to mynter kastes, den ene etter den andre. Det blir bedt om:

a) Angi om det er et tilfeldig eksperiment eller tvert imot et deterministisk eksperiment.

b) Hva er prøveområdet til dette eksperimentet?

c) Angi hele hendelsen A, tilsvarende eksperimentet har et ansikts- og stempelresultat.

d) Beregn sannsynligheten for at hendelsen inntreffer til.

e) Finn til slutt sannsynligheten for at hendelsen B: ikke vises ansikt til resultatet.

Løsning 

a) Det er et tilfeldig eksperiment fordi det ikke er noen måte å forutsi hva som vil være et resultat av en lansering av de to myntene.

b) Prøveområdet er settet med alle mulige resultater:

S = (c, c), (c, s), (s, c), (s, s)

c) Hendelse A, i saken som er gitt, kan ha følgende resultater:

A = (c, s), (s, c)

d) Sannsynligheten for hendelse A oppnås fra å dele antall elementer i settet A mellom antall elementer i settet som tilsvarer prøveområdet:

P (a) = 2/4 = ½ = 0.5 = 50%

e) Settet med mulige resultater som tilsvarer hendelse B (ikke ser ut til at resultatet) er:

Kan tjene deg: perfekt firkantet trinomial

B = (s, s)

Så sannsynligheten for at hendelse B skjer i et essay er forholdet mellom antall mulige resultater av B mellom antall totale tilfeller:

P (b) = ¼ = 0.25 = 25%.

Eksempel 2

En pose inneholder 10 hvite kuler og 10 svarte klinkekuler. Fra posen fjernes de tilfeldig. 

a) Bestem prøveområdet til dette tilfeldige eksperimentet.

b) Bestem settet med resultater som tilsvarer hendelsen som er at det etter eksperimentet er to svarte klinkekuler.

c) Hendelse B er å skaffe minst to svarte klinkekuler, bestemme sett B av resultater for denne hendelsen.

d) Hva er sannsynligheten for at hendelsen finner sted?

e) Finn sannsynligheten for at hendelsen B.

f) Bestem sannsynligheten for at resultatet av det tilfeldige eksperimentet er at minst en svart marmor. Denne hendelsen vil bli kalt C.

Figur 2. Svarte og svarte klinkekuler for tilfeldige eksperimenter. Kilde: Needpix.

Løsning på

For å bygge prøveområdet er det nyttig å lage et trediagram, for eksempel det som er vist i figur 3:

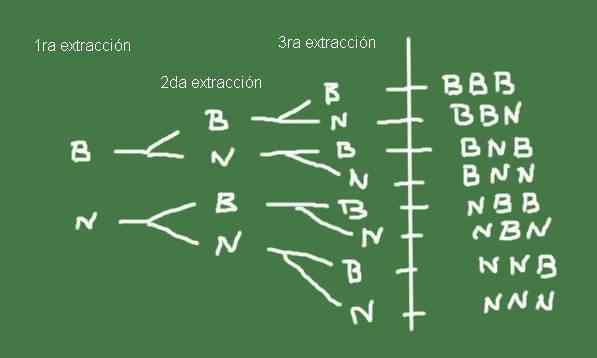Figur 3. Trediagram for eksempel 2. Utarbeidet av Fanny Zapata.

Ω -settet med mulige resultater av å trekke ut tre klinkekuler fra en pose med samme antall svarte og svarte klinkekuler, er nettopp prøveområdet til dette tilfeldige eksperimentet.

Ω = (b, b, b), (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n) , (n, n, b), (n, n, n)

Løsning b

Settet med mulige resultater som tilsvarer hendelse A, som består av å ha to svarte klinkekuler er:

Kan tjene deg: Summen av Riemann: Historie, formler og egenskaper, øvelser

A = (b, n, n), (n, b, n), (n, n, b)

Løsning c

Hendelse B er definert som: "å ha minst to svarte klinkekuler etter å ha gjort tilfeldig utvinning av tre av dem". Settet med mulige resultater for hendelse B er:

B = (b, n, n), (n, b, n), (n, n, b), (n, n, n)

Løsning d

Sannsynligheten for å ha hendelse A er forholdet mellom antall mulige resultater for denne hendelsen, og det totale antallet mulige resultater, det vil si antall utvalgsplasselementer.

P (a) = n (a) / n (ω) = 3/8 = 0.375 = 37.5%

Så det er 37.5% sannsynlighet for å ha to svarte klinkekuler etter å ha trukket ut tre klinkekuler fra sekken tilfeldig. Men merk at vi på ingen måte kan forutsi det nøyaktige resultatet av eksperimentet.

Løsning e

Sannsynligheten for at hendelse B er gitt, bestående av minst en svart marmor er:

P (b) = n (b) / n (ω) = 4/8 = 0.5 = 50%

Dette betyr at muligheten for hendelse B er lik sannsynligheten som ikke oppstår. 

Løsning f

Sannsynligheten for å oppnå minst en svart marmor, etter å ha trukket ut tre av dem, er lik 1 mindre sannsynligheten for at resultatet er "de tre hvite klinkekuler".

P (c) = 1 - p (b b b) = 1 - ⅛ = ⅞ = 0.875 = 87.5%

Nå kan vi bekrefte dette resultatet, og bemerker at antallet muligheter gitt hendelsen C er lik antall elementer av mulige resultater for hendelse C:

C = (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n), (n, n, b) , (n, n, n)

N (c) = 7

P (c) = n (c) / n (ω) = ⅞ = 87.5%

Referanser

1. Canalphi. Tilfeldig eksperiment. Gjenopprettet fra: YouTube.com.
2. Mathemovil. Tilfeldig eksperiment. Gjenopprettet fra: YouTube.com
3. Pishro Nick h . Introduksjon til sannsynlighet. Hentet fra: sannsynlighetskurs.com
4. Ross. Sannsynlighet og statistikk for ingeniører. Mc-Graw Hill.
5. Wikipedia. Eksperiment (sannsynlighetsteori). Hentet fra: i.Wikipedia.com
6. Wikipedia. Deterministisk hendelse. Gjenopprettet fra: er. Wikipedia.com
7. Wikipedia. Tilfeldig eksperiment. Gjenopprettet fra: er.Wikipedia.com