Empirisk styre hvordan du bruker det, hva er det for, løst øvelser

EN Empirisk styre Det er resultatet av den praktiske erfaringen og observasjonen av det virkelige liv. For eksempel kan du vite at fuglearter kan observeres på visse steder i hver gang på året, og at observasjon kan etableres en "regel" som beskriver livssyklusene til disse fuglene.

I statistikk refererer den empiriske regelen til formen for gruppering av observasjoner rundt en sentral verdi, gjennomsnittlig eller gjennomsnitt, i standardavviksenheter.

Anta at du har en gruppe mennesker med en gjennomsnittlig høyde på 1.62 meter og et standardavvik på 0.25 meter, da vil den empiriske regelen tillate å definere for eksempel hvor mange mennesker som vil være i et intervall av gjennomsnittet mer eller mindre et standardavvik?

I henhold til regelen er 68% av dataene mer eller mindre et standardavvik for gjennomsnittet, det vil si at 68% av gruppefolk vil ha en høyde mellom 1.37 (1.62-0.25) og 1.87 (1.62+0.25) meter.

[TOC]

Hvor kommer den empiriske regelen fra?

Den empiriske regelen er en generalisering av Tchebyshevs teorem og normalfordeling.

Tchebyshev teorem

Tchebyshevs teorem sier at: for en viss verdi av k> 1, sannsynligheten for at en tilfeldig variabel er blant gjennomsnittet mindre k ganger standardavviket, og gjennomsnittlig flere k ganger, er standardavviket større enn eller lik (1 -1 /k²).

Fordelen med dette teoremet er at det gjelder diskrete eller kontinuerlige tilfeldige variabler med enhver sannsynlighetsfordeling, men regelen definert fra den er ikke alltid veldig presis, fordi det avhenger av symmetrien i distribusjonen. Jo mer asymmetrisk fordeling av den tilfeldige variabelen, mindre justert til regelen vil være dens oppførsel.

Den empiriske regelen definert fra dette teoremet er:

Hvis k = √2, sies det at 50% av dataene er i intervallet: [µ - √2 s, µ + √2 s]

Hvis k = 2, sies det at 75% av dataene er i intervallet: [µ - 2 s, µ + 2 s]

Hvis k = 3, sies det at 89% av dataene er i intervallet: [µ - 3 s, µ + 3 s]

Normal distribusjon

Normalfordelingen, eller Gauss Bell, gjør det mulig å etablere den empiriske regelen eller regel 68 - 95 - 99.7.

Kan tjene deg: proporsjon

Regelen er basert på sannsynlighetene for forekomst av en tilfeldig variabel med intervaller mellom gjennomsnittet mindre, to eller tre standardavvik og gjennomsnittet pluss ett, to eller tre standardavvik.

Den empiriske regelen definerer følgende intervaller:

68.27% av dataene er i intervallet: [µ - s, µ + s]

95.45% av dataene er i intervallet: [µ - 2s, µ + 2s]

99.73% av dataene er i intervallet: [µ - 3s, µ + 3s]

I figuren kan du se hvordan disse intervallene blir presentert og forholdet mellom dem ved å øke bredden på den grafiske basen.

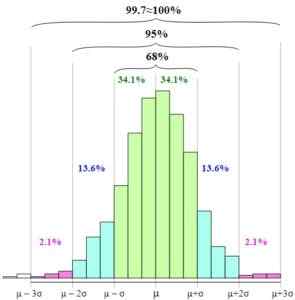Empirisk styre. Melikamp [CC By-SA 4.0 (https: // creativecommons.org/)] Standardiseringen av den tilfeldige variabelen, det vil si uttrykk for den tilfeldige variabelen når det til en.

Derfor definerer anvendelsen av den empiriske regelen om skala av en standard normal variabel, z, følgende intervaller:

68.27% av dataene er i intervallet: [-1, 1]

95.45% av dataene er i intervallet: [-2, 2]

99.73% av dataene er i intervallet: [-3, 3]

Hvordan anvende den empiriske regelen?

Den empiriske regelen lar deg forkorte beregninger når du jobber med en normalfordeling.

Anta at en gruppe på 100 universitetsstudenter har en gjennomsnittsalder på 23 år, med et standardavvik på 2 år. Hvilken informasjon tillater den empiriske regelen?

Bruken av den empiriske regelen innebærer å følge trinnene:

1- Bygg regelintervallene

Siden gjennomsnittet er 23 og standardavviket er 2, er intervallene:

[µ - s, µ + s] = [23 - 2, 23 + 2] = [21, 25]

[µ - 2s, µ + 2s] = [23 - 2 (2), 23 + 2 (2)] = [19, 27]

[µ - 3s, µ + 3s] = [23 - 3 (2), 23 + 3 (2)] = [17, 29]

2- Beregn antall studenter i hvert intervall i henhold til prosentene

(100)*68.27% = 68 studenter omtrent

(100)*95.45% = omtrent 95 studenter

(100)*99.73% = 100 studenter

3- Alder intervaller er assosiert med mengden studenter og tolket

Minst 68 studenter er mellom 21 og 25 år gamle.

Kan tjene deg: Beskrivende statistikk: Historie, egenskaper, eksempler, konsepter

Minst 95 studenter er mellom 19 og 27 år gamle.

Praktisk talt 100 studenter er mellom 17 og 29 år gamle.

Hva er den empiriske regelen for?

Den empiriske regelen er en rask og praktisk måte å analysere statistiske data, og er stadig mer pålitelig i den grad distribusjonen er nær symmetri.

Nytten av det avhenger av feltet den brukes i, og spørsmålene som oppstår. Det er veldig nyttig å vite at forekomsten av verdier av tre standardavvik er nesten usannsynlig under eller over gjennomsnittet, selv for ikke -normale distribusjonsvariabler, minst 88.8% av tilfellene er i de tre Sigma -intervallene.

I samfunnsvitenskapene er et generelt avgjørende resultat intervallet for gjennomsnittet mer eller mindre to Sigma (95%), mens i partikkelfysikk krever en ny effekt et fem Sigmas -intervall (99.99994%) for å bli betraktet som en oppdagelse.

Løste øvelser

Kaniner i reservatet

I en dyrelivsreserve er det anslått at det er i gjennomsnitt 16.000 kaniner med et standardavvik på 500 kaniner. Hvis distribusjonen av variabelt 'antall kaniner i reservatet' er ukjent, er det mulig.000 og 17.000 kaniner?

Intervallet kan presenteres i disse begrepene:

15000 = 16000 - 1000 = 16000 - 2 (500) = µ - 2 s

17000 = 16000 + 1000 = 16000 + 2 (500) = µ + 2 s

Derfor: [15000, 17000] = [µ - 2 s, µ + 2 s]

Bruker Tchebyshevs teorem, det er sannsynlighet for minst 0.75 at befolkningen av kaniner i dyrelivsreserven er mellom 15.000 og 17.000 kaniner.

Gjennomsnitt av barn fra et land

Gjennomsnittsvekten til ett år gamle barn fordeles normalt med et gjennomsnitt på 10 kilo og et standardavvik på omtrent 1 kilo.

a) estimere prosentandelen av ett år med barn i landet som har en gjennomsnittlig vekt mellom 8 og 12 kilo.

8 = 10 - 2 = 10 - 2 (1) = µ - 2 s

12 = 10 + 2 = 10 + 2 (1) = µ + 2 s

Derfor: [8, 12] = [µ - 2s, µ + 2s]

Det kan tjene deg: Tukey Test: Det som er i tilfelle av eksempel løst trening

I følge den empiriske regelen kan det bekreftes at 68.27% av barna i landet har mellom 8 og 12 kilo vekt.

b) Hva er sannsynligheten for å finne et årlig barn på 7 kilo eller mindre vekt?

7 = 10 - 3 = 10 - 3 (1) = µ - 3 s

Det er kjent at 7 kilo vekt representerer verdien µ - 3s, så vel som det er kjent at 99.73% av barna er mellom 7 og 13 kilo vekt. Som bare etterlater 0.27% av de totale barna for ytterpunktene. Halvparten av dem, 0.135%, har 7 kilo vekt eller mindre og den andre halvparten, 0.135%, har 11 kilo vekt eller mer.

Så det kan konkluderes med at det er sannsynlighet for 0.00135 at et barn har 7 kilo vekt eller mindre.

c) Hvis befolkningen i landet når 50 millioner innbyggere og barna på 1 år?

9 = 10 - 1 = µ - S

11 = 10 + 1 = µ + s

Derfor: [9, 11] = [µ - s, µ + s]

I følge den empiriske regelen, 68.27% av ett år gammel barn er i intervallet [µ -s, µ + s]

I landet er det 500 000 barn på ett år (1% av 50 millioner), så 341350 barn (68.27% av 500000) har mellom 9 og 11 kilo vekt.

Referanser

1. Abraira, v. (2002). Standardavvik og standardfeil. Smergen Magazine. Nettinnhenting.Arkiv.org.
2. Freund, r.; Wilson, w.; Mohr, d. (2010). Statistiske metoder. Tredje utg. Academic Press-ELSEVIER INC.
3. Alicante Server (2017). Empirisk regel (statistiske termer). Ordliste gjenopprettet.server-alive.com.
4. Lind, d.; Marchal, w.; Wathen, s. (2012). Statistikk gjaldt næringsliv og økonomi. Tiende utg. McGraw-Hill/Inter-American fra Mexico S. TIL.
5. Salinas, h. (2010). Statistikk og sannsynligheter. Gjenopprettet fra UDA.Cl.
6. Sokal, r.; Rohlf, f. (2009). Introduksjon til biostatistikk. Second Ed. Dover Publications, Inc.
7. Spiegel, m. (1976). Sannsynlighet og statistikk. Schaum -serien. McGraw-Hill/Inter-American fra Mexico S. TIL.
8. Spiegel, m.; Stephens, l. (2008). Statistikk. Fjerde utg. McGraw-Hill/Inter-American fra Mexico S. TIL.
9. Stat119 Review (2019). Empirisk løse regel spørsmål. Hentet fra STAT119Review.com.
10. (2019). 68-95-99.7 Regel. Innhentet fra.Wikipedia.org.