Millikan eksperimentprosedyre, forklaring, betydning

Han Millikan -eksperiment, utført av Robert Millikan (1868-1953) med sin student Harvey Fletcher (1884-1981), begynte i 1906 og hadde som mål å studere egenskapene til den elektriske ladningen, og analyserte bevegelsen av tusenvis av oljedråper midt i en uniform elektrisk felt.

Konklusjonen var at den elektriske ladningen ikke hadde en vilkårlig verdi, men at den kom i multipler på 1.6 x 10^-19 C, som er den grunnleggende belastningen på elektronet. I tillegg ble elektronmassen funnet.

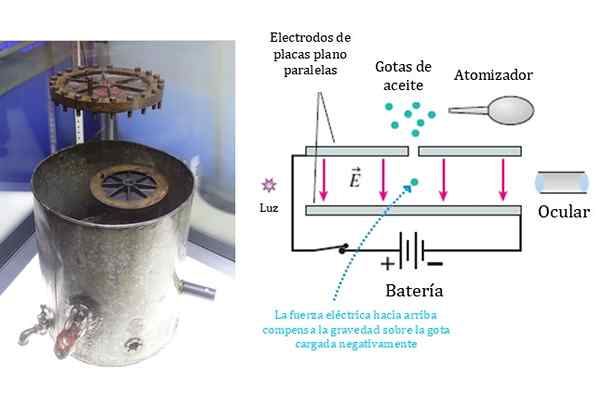
Figur 1. Til venstre for den opprinnelige enheten som brukes av Millikan og Fletcher i eksperimentet deres. Til høyre for en forenklet ordning av det samme. Kilde: Wikimedia Commons/F. Zapata,

Tidligere den fysiske J.J. Thompson hadde funnet eksperimentelt belastnings-land-forholdet til denne elementære partikkelen, som han kalte "corpuscle", men ikke verdiene i hver størrelse hver for seg.

Fra denne belastningen - masseforhold og elektronbelastning, ble verdien av massen bestemt: 9.11 x 10^-31 Kg.

For å oppnå deres formål, serverte Millikan og Fletcher en forstøver som en fin tåke med oljedråper ble sprayet. Noen av dråpene ble elektrisk lastet takket være friksjon i sprøyten.

Lastede dråper satte seg sakte på parallelle flate plakkelektroder, der noen få passerte gjennom et lite hull i den øvre platen, som vist i skjemaet i figur 1.

Inne i parallelle plater er det mulig å lage et jevnt elektrisk felt og vinkelrett på platene, hvis størrelse og polaritet ble kontrollert ved å modifisere spenningen.

Dråpens oppførsel ble observert ved å belyse innsiden av platene med et sterkt lys.

[TOC]

Forklaring av eksperimentet

Hvis dråpen har en belastning, utøver feltet som opprettes mellom platene en kraft på det som motvirker tyngdekraften.

Og hvis det også klarer å bli suspendert, betyr det at feltet utøver en vertikal kraft opp, som nøyaktig balanserer til tyngdekraften. Denne tilstanden vil avhenge av verdien av q, belastningen på gikt.

Faktisk observerte Millikan at etter å ha slått på feltet, noen dråper ble suspendert, begynte andre å klatre eller fortsatte å gå ned.

Justere verdien av det elektriske feltet -gjennom variabel motstand, for eksempel -et fall kan tillates å forbli suspendert innenfor platene. Selv om det i praksis ikke er lett å oppnå, i tilfelle det skjedde, er det bare styrken som utøves av felt- og tyngdekraften på dråpen.

Kan tjene deg: Absorbans: Hva er, eksempler og øvelser løst

Hvis massen av dråpen er m Og belastningen er q, Å vite at kraften er proporsjonal med det påførte størrelsesfeltet OG, Newtons andre lov slår fast at begge styrkene må være balansert:

mg = q.OG

Q = mg/e

Verdien av g, Selerasjonen av tyngdekraften er kjent, så vel som størrelsen OG av feltet, som avhenger av spenningen V etablert mellom platene og separasjonen mellom disse L, som:

E = v/l

Spørsmålet var å finne massen av den lille dråpen olje. Når dette er oppnådd, må du bestemme belastningen q Det er helt mulig. Naturligvis det m og q De er henholdsvis massen og belastningen på slippet av olje, ikke elektronet.

Men ... fallet er lastet fordi det mister eller får elektroner, så verdien er relatert til belastningen på nevnte partikkel.

Massen til oljedråpen

Millikan og Fletchers problem var å bestemme massen av en dråpe, en oppgave som ikke er lett på grunn av den lille størrelsen på den.

Når du kjenner til oljen. Men volumet var også veldig lite, så de konvensjonelle metodene var ikke nyttige.

Imidlertid visste forskere at slike små gjenstander ikke faller fritt, siden motstanden i luften eller miljøet, griper inn ved å bremse bevegelsen deres. Selv om partikkelen når den frigjøres med off -feltet opplever en akselerert vertikal bevegelse og ned, ender den opp med å falle med konstant hastighet.

Ved denne hastigheten kalles det "terminalhastighet" eller "grensehastighet", som i tilfelle av en sfære, avhenger av dens radius og luftviskositet.

I mangel av felt målte Millikan og Fletcher tiden dråpene tok til å falle. Forutsatt at dråpene var sfæriske og med verdien av luftens viskositet, ble de fikset for å bestemme radius indirekte fra terminalhastigheten.

Denne hastigheten bruker Stokes lov og her er ligningen:

 Hvor:

-v_t er terminalhastigheten

-R Det er radius av gikt (sfærisk)

-η Det er lufts viskositet

-ρ Det er tettheten av gikt

Betydning

Millikans eksperiment var avgjørende, fordi det viste flere viktige aspekter i fysikken:

I) Elementærbelastningen er elektronet, hvis verdi er 1.6 x 10 ^-19 C, en av vitenskapens grunnleggende konstanter.

Ii) Enhver annen elektrisk lading kommer i multipler av den grunnleggende belastningen.

Kan tjene deg: Parabolsk skudd: Kjennetegn, formler og ligninger, eksempler

Iii) å kjenne til ladningen til elektronet og belastningsmasa-forholdet til j.J. Thomson, det var mulig å bestemme elektronmassen.

Iii) Hos partikler så små som elementære partikler er gravitasjonseffekter ubetydelige mot elektrostatisk.

Figur 2. Millikan i forgrunnen til høyre, ved siden av Albert Einstein og andre bemerkelsesverdige fysikere. Kilde: Wikimedia Commons.

Millikan mottok Nobelprisen i fysikk i 1923 for disse funnene. Eksperimentet hans er også relevant fordi han bestemte disse grunnleggende egenskapene til den elektriske ladningen, basert på enkel instrumentering og anvendelse av lover som er kjent for alle.

Imidlertid ble Millikan kritisert for å ha utelukket mange observasjoner i eksperimentet sitt, uten tilsynelatende grunn, for å redusere den statistiske feilen til resultatene, og at de var mer "presentable".

Faller med forskjellige belastninger

Millikan målte mange dråper i eksperimentet sitt, og ikke alle var olje. Han testet også med kvikksølv og glyserin. Som sagt begynte eksperimentet i 1906 og utvidet seg i noen år. Tre år senere, i 1909, ble de første resultatene publisert.

I løpet av denne tiden skaffet han seg en rekke belastninger lastet ved å påvirke x -strømmer gjennom platene, for å ionisere luften mellom dem. På denne måten frigjøres lastede partikler som dråper kan godta.

I tillegg konsentrerte den seg ikke utelukkende på suspenderte dråper. Millikan observerte at når dråpene utgjorde, varierte også stigningshastigheten i henhold til belastningen som ble levert.

Og hvis dråpen gikk ned, denne ekstra ekstra belastningen takket være intervensjonen fra x -strålene, varierte ikke hastigheten, fordi noen masse elektroner som ble lagt til dråpen er små bokstaver, sammenlignet med massen til selve dråpen.

Uansett hvor mye belastning han la til, fant Millikan at alle dråper anskaffet hele multipler av en viss verdi, som er og, Den grunnleggende enheten, som vi har sagt, er elektronbelastningen.

Millikan oppnådde opprinnelig 1.592 x 10^-19 C for denne verdien, litt lavere enn den som for øyeblikket er akseptert, som er 1.602 x 10^-19 C. Årsaken kan ha vært verdien den ga til luftviskositeten i ligningen for å bestemme terminalhastigheten til dråpen.

Eksempel

Leviterer en dråpe olje

Vi ser følgende eksempel. En dråpe olje har tetthet ρ = 927 kg/m³ og frigjøres midt i elektroder med det elektriske feltet av. Dråpen når raskt terminalhastigheten, hvorved radius bestemmes, hvis verdi viser seg å være r = 4,37 x10^-7 m.

Kan tjene deg: Fordeler og ulemper ved friksjon

Det enhetlige feltet er slått på, er rettet vertikalt opp og har 9,66 kN/C -størrelse . På denne måten oppnås det at dråpen er suspendert i ro.

Det blir bedt om:

a) Beregn slippbelastningen

b) Finn hvor mange ganger den elementære belastningen er inneholdt i slippbelastningen.

c) Bestem om mulig, tegnet på belastningen.

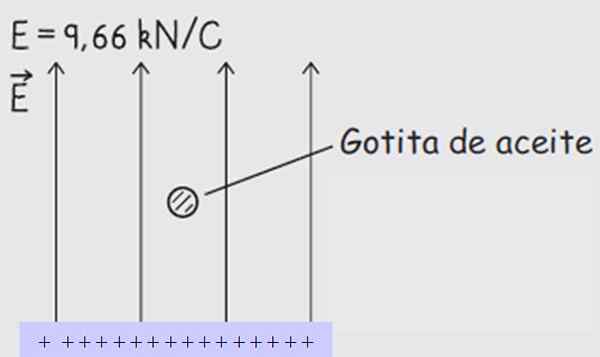Figur 3. En dråpe olje midt i et konstant elektrisk felt. Kilde: Fundamentals of Physics. Rex-Wolfson.

Løsning på

Tidligere ble følgende uttrykk trukket ut for et hvilepågang:

Q = mg/e

Når du kjenner til tettheten og radius av gikt, bestemmes massen av dette:

ρ = m /v

V = (4/3) πr³

Derfor:

m = ρ.V = ρ. (4/3) πr³= 927 kg/m³. (4/3) π.(4.37 x10^-7 m)³= 3.24 x 10^-16 kg

Derfor er belastningen på dråpen:

Q = mg/e = 3.24 x 10^-16 kg x 9.8 m/s²/9660 n = 3.3 x 10^-19 C

Løsning b

Å vite at den grunnleggende belastningen er e = 1.6 x 10 ^-19 C, belastningen oppnådd i forrige seksjon er delt på denne verdien:

n = q/e = 3.3 x 10^-19 C/1.6 x 10 ^-19 C = 2.05

Resultatet er at belastningen på dråpen er omtrent dobbelt (n≈2) av elementær belastning. Det er ikke akkurat det dobbelte, men dette lille avviket skyldes den uunngåelige tilstedeværelsen av den eksperimentelle feilen, samt avrundingen i hver av de tidligere beregningene.

Løsning c

Ja, det er mulig å bestemme tegnet på belastningen, takket være det faktum at uttalelsen gir informasjon om feltets retning, som er rettet vertikalt oppover, akkurat som styrken.

De elektriske feltlinjene starter alltid fra positive belastninger og ender i negative belastninger, derfor er den nedre platen lastet med skilt + og den over med et skilt - (se figur 3).

Siden dråpen er rettet mot ovennevnte plate drevet av feltet, og siden det motsatte skiltbelastningen er tiltrukket, må dråpen ha en positiv ladning.

Det er faktisk ikke lett å få det suspenderte fallet. Så Millikan brukte de vertikale forskyvningene (UPS.

Denne ervervede belastningen er proporsjonal med elektronbelastningen, som vi allerede har sett, og kan beregnes med stigningen og nedstigningstidene, massen av dråpen og verdiene til g og OG.

Referanser

1. Åpent sinn. Millikan, fysikeren som kom for å se elektronet. Gjenopprettet fra: bbvaopenmind.com
2. Rex, a. 2011. Fundamentals of Physics. Pearson.
3. Tippens, p. 2011. Fysikk: konsepter og applikasjoner. 7. utgave. McGraw Hill.
4. Amrit.  Millikan's Oil Drop -eksperiment. Gjenopprettet fra: VLAB.Amrit.Edu
5. Wake Forest College. Millikan's Oil Drop -eksperiment. Gjenopprettet fra: WFU.Edu