Vanlig faktor for gruppering av begreper eksempler, øvelser

Han Vanlig faktor for gruppering av vilkår Det er en algebraisk prosedyre som tillater å skrive noen algebraiske uttrykk i form av faktorer. For å oppnå dette målet, må uttrykket først være praktisk å gruppere og observere at hver gruppe som således dannes, faktisk har en vanlig faktor.

Å bruke teknikken krever riktig praksis, men på kort tid er det mulig å dominere. La oss først se et illustrerende eksempel beskrevet trinn for trinn. Da kan leseren bruke det de lærte i hver av øvelsene som vil vises etter.

Figur 1. Fjern vanlig faktor for gruppering av begreper letter arbeidet med algebraiske uttrykk. Kilde: Pixabay.

Anta for eksempel at du må faktorere følgende uttrykk:

2x² + 2xy - 3zx - 3zy

Dette algebraiske uttrykket består av 4 monomialer eller termer, atskilt med tegn + og -, nemlig:

2x², 2xy, -3zx, -3zy

Å observere nøye, X er vanlig for de tre første, men ikke til den siste, mens og er felles for den andre og den fjerde, og Z er felles for den tredje og den fjerde.

Så i prinsippet er det ingen felles faktor til de fire begrepene samtidig, men hvis de er gruppert som det vil vises i følgende avsnitt, kan man hjelpe deg med å skrive uttrykket som produkt av to eller flere faktorer.

[TOC]

Eksempler

Faktor uttrykket: 2x² + 2xy - 3zx - 3zy

Trinn 1: Gruppe

2x² + 2xy - 3zx - 3zy = (2x² + 2xy) + (-3zx - 3zy)

Trinn 2: Fjern den vanlige faktoren fra hver gruppe

2x² + 2xy - 3zx - 3zy =

= (2x² + 2xy) - (3zx + 3zy) =

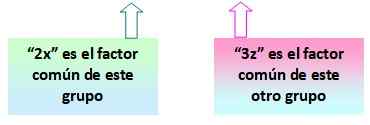
= 2x (x+y) - 3z (x+y)

YoMportante: Det negative tegnet er også en vanlig faktor som må tas i betraktning.

Kan tjene deg: Vektorrom: base og dimensjon, aksiomer, egenskaper

Legg nå merke til at parentesen (x+y) gjentas i de to begrepene oppnådd når du grupperer. Det er den vanlige faktoren som lette etter.

Trinn 3: Faktoriser alt uttrykket

2x² + 2xy - 3zx - 3zy = (x+y) (2x - 3z)

Med det forrige resultatet er målet med faktoriseringen nådd, noe som er ingen ringere enn å transformere et algebraisk uttrykk basert på summer og subtraksjon av termer, i et produkt av to eller flere faktorer, i vårt eksempel, av: (x+ y) og (2x - 3Z).

Viktige spørsmål om den vanlige gruppefaktoren

Spørsmål 1: Hvordan vite at resultatet er riktig?

Svar: Distributiv eiendom brukes på det oppnådde resultatet, og etter å ha redusert og forenklet, må uttrykket som er oppnådd sammenfalle med originalen, hvis ikke, det er en feil.

I forrige eksempel fungerer det omvendt med resultatet, for å bekrefte at det er bra:

(x+y) (2x - 3z) = 2x² -3zx +2xy - 3zy

Ettersom rekkefølgen på tilleggene ikke endrer summen, etter å ha brukt distribusjonseiendommen, alle de opprinnelige vilkårene, er det tegn inkludert, derfor er faktoriseringen riktig.

Spørsmål 2: Kunne du ha gruppert på en annen måte?

Svar: Det er algebraiske uttrykk som innrømmer mer enn en form for gruppering og andre som ikke gjør det. I det valgte eksemplet kan leseren prøve andre muligheter, for eksempel gruppering:

2x² + 2xy - 3zx - 3zy = (2x²- 3zx) + (2xy - 3zy)

Og du kan se at resultatet er det samme som oppnådd her. Å finne den optimale gruppen er et spørsmål om praksis.

Kan tjene deg: Cotangent avledet: beregning, demonstrasjon, øvelser

Spørsmål 3: Hvorfor er det nødvendig å få felles faktor fra et algebraisk uttrykk?

Svar: Fordi det er applikasjoner der det faktoriserte uttrykket letter beregninger. Anta for eksempel at du vil gjøre 2x² + 2xy - 3zx - 3zy lik 0. Hva ville være mulighetene?

For å svare på denne bekymringen, er den faktoriserte versjonen mye mer nyttig enn den opprinnelige utviklingen i termer. Det oppstår slik:

(x+y) (2x - 3z) = 0

En mulighet for at uttrykket er verdt 0 er at x = -y, uavhengig av verdien av z. Og den andre er at x = (3/2) z, uten å ha noe spørsmål om verdien av y.

Øvelser

- Oppgave 1

Få vanlig faktor for følgende uttrykk ved gruppering av begreper:

øks+ay+bx+av

Løsning

De to første er gruppert, med den vanlige faktoren "A" og de to siste med den vanlige faktoren "B":

AX+AY+BX+BY = A (x+y)+B (x+y)

Når dette er gjort, avsløres en ny felles faktor, som er (x+y), slik at:

AX+AY+BX+BY = A (x+y)+B (x+y) = (x+y) (a+b)

En annen måte å gruppere

Dette uttrykket innrømmer en annen måte å gruppere på. La oss se hva som skjer hvis vilkårene er omorganisert og en gruppe er laget som de inneholder X og en annen med de som inneholder og:

AX +AY +BX +BY = AX +BX +AY +BY = X (A +B) +Y (A +B)

På denne måten er den nye vanlige faktoren (A+B):

AX+AY+BX+BY = AX+BX+AY+BY = x (a+b)+y (a+b) = (x+y) (a+b)

Det fører til samme resultat av den første måten å gruppere som det ble testet.

- Oppgave 2

Det er påkrevd å skrive følgende algebraiske uttrykk som de to faktorproduktet:

3³ - 3²B+9AB²-til²+AB-3B²

Kan tjene deg: Coplanares Points: Ligning, eksempel og løste øvelser

Løsning

Dette uttrykket inneholder 6 begreper. La oss prøve å gruppere første og fjerde, andre og tredje og til slutt femte og sjette:

3³ - 3²B+9AB²-til²+AB-3B² = (3³ -til²) + (- 3²B+9AB²) + (AB-3B²)

Nå er hver parentese faktor:

= (3³ -til²) + (- 3²B+9AB²) + (Ab -3b²) = a² (3A -1) + 3AB (3B -A) + B (A -3B)

Ved første øyekast ser det ut til at situasjonen har vært komplisert, men leseren skal ikke frarådes, siden vi kommer til å omskrive forrige periode:

til² (3a -1) + 3Ab (3B -A) + B (A -3b) = A² (3A - 1) + 3AB (3B -A) - B (3B -A)

De to siste begrepene har nå en felles faktor, som er (3B-A), slik at de kan faktoriseres. Det er veldig viktig å ikke miste synet på første periode til² (3a - 1), som må fortsette å følge alt som legger til, slik at du ikke jobber med ham:

til² (3A - 1) + 3AB (3B -A) - B (3B -A) = A² (3A-1) + (3B-A) (3AB-B)

Uttrykket er redusert til to begreper, og en ny felles faktor blir oppdaget i den siste, som er "B". Nå gjenstår det:

til² (3a-1) + (3b-a) (3ab-b) = a² (3A-1) +B (3B-A) (3A-1)

Den neste vanlige faktoren for å vises er 3. - 1:

til² (3a - 1) +B (3b -a) (3a -1) = (3a - 1) [a² + B (3B-A)]

Eller hvis du foretrekker uten firkantede parenteser:

(3. - 1) [a² + B (3b -a)] = (3a - 1) (a² -AB + 3B²)

Kan leseren finne en annen måte å gruppere på som fører til samme resultat?

Figur 2. Foreslåtte faktoriseringsøvelser. Kilde: f. Zapata.

Referanser

1. Baldor, a. 1974. Elementær algebra. Venezuelanske kulturelle s.TIL.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Hovedtilfeller av faktorisering. Gjenopprettet fra: Julioprofe.nett.
4. Unam. Grunnleggende matematikk: Faktorisering ved å gruppere termer. Fakultet for regnskap og administrasjon.
5. Zill, d. 1984. Algebra og trigonometri. MacGraw Hill.