Emballasjefaktor

Emballasjefaktoren er en brøkdel som indikerer hvor mye volum partiklene okkuperer, enten atomer, ioner eller molekyler, i det indre rommet til en krystall. Verdien er alltid mindre enn 1, som blir 100% av glassvolumet; Mer nøyaktig er den enhetlige cellen, som er den minste representasjonen av hele glasset.

En 100% pakningsfaktor betyr at partiklene okkuperer volumet av den enhetlige cellen i sin helhet. Fysisk er det umulig for dette å skje, fordi det for eksempel vil innebære at atomene deformerer sine radioer og oppløses som om de var en "elektronisk væske". Geometrien til atomer, sfærisk for enkelhets skyld, resulterer alltid i tomme rom under emballasje.

Når det skjer i søte dispenseringsmaskiner, forteller emballasjefaktoren oss hvordan "stram" er partiklene i en krystall: jo større er den, jo mer tyggegummi eller atomer, vil det være i verdensrommet

I definisjonen av emballasjefaktoren antas det at atomene består av stive kuler, for eksempel tannkjøtt eller godteriballer fra en dispensert maskin (overlegen bilde). Blant sfærene vil det alltid være hule rom der mindre kuler (urenheter eller tilsetningsstoffer kan snekes).

Hvis vi øker emballasjefaktoren, vil kulene bli presset og snu det mest kompakte og tette glasset; eller på den annen side, mer deformerbar, som med formbare og duktile metaller.

Emballasjefaktoren gjelder for alle typer glass. Imidlertid kan beregningen bli litt kjedelig, så den vil bare bli vurdert for atomkrystaller med enkle strukturer.

[TOC]

Emballasjefaktorformel

Emballasjefaktoren uttrykkes vanligvis som prosenter. For eksempel, hvis verdien er 40%, betyr det at partiklene knapt okkuperer 40% av den totale plassen til enhetscellen; eller hva som er det samme som å si at 60% av glasset er "tomt".

Ovennevnte tydeliggjør hva som er formelen for beregning av denne faktoren:

• Ugly = (volum av atomer)/ (enhetscellevolum)

Der stygg betyr Atomisk pakningsfaktor, Hva er de enkleste krystaller.

Volumet av enhetscellen avhenger av dens parametere (for eksempel lengden på sidene), som den videreføres med enkel geometri for å beregne volumet. Atomene er derimot de som definerer cellen, så det er mulig å uttrykke dimensjonene til det samme fra atomradioene, som det vil bli sett i de neste seksjonene.

Det kan tjene deg: Racemic Mix: Chirality, Eksempler

Når det gjelder volumet av atomer, er det totale antallet av dem som er til stede i enhetscellen (1, 2, 3 osv.), så vel som dens sfæriske geometri. Derfor modifiseres formelen litt:

Ugly = (Nº Atoms) (atomvolum)/ (enhetscellevolum)

For å beregne stygg, må du bestemme da nei, v_atom og v_{Unitary Cell}.

Enkel kubikk

Enkel kubisk enhetscelle. Kilde: CCC_CRYSTAL_CELL_ (OPAQUE).SVG: *COBIQUE_CENTRE_ATOMES_PAR_MAILLE.SVG: Cdang (Original Idea og SVG Execution), Samuel Dupré (3D Odeeling with SolidWorks) HEPIVE WORK: Daniele Pugliesi (talk) Luft Work: Daniele Pugliesi, CC By-SA 3.0, via Wikimedia Commons

Den enkleste enhetlige cellen av alle er den enkle kubikk. I den har vi noen porsjoner atomer i hvert av hjørnene. Hvis vi ser, vil vi legge merke til at lengden til Fra denne cellen er den lik 2R, siden det er atomene som definerer cellen. Så volumet av enhetscellen vil være lik:

V_{Unitary Cell} = til³ (volum av en kube)

= (2r)³

= 8r³

I mellomtiden vil volumet av atomet være lik:

V_atom = (4/3) πr³ (volum av en sfære)

Hvert av hjørnene deles av ytterligere 8 naboenhetsceller. Derfor har vi en 1/8 brøkdel i hvert hjørne, og har 8 av dem, vi bryr oss ikke 1 atom per enhetscelle (1/8 x 8 = 1).

Emballasjefaktoren er:

Stygg = (1) (4/3) πr³ /8r³

= π/6 ≈ 52%

Det vil si at i en enkel kubikkcelle okkuperer atomene 52% av hele glassvolumet.

Kubikk sentrert i kroppen

Bestemmelse av cellevolumet

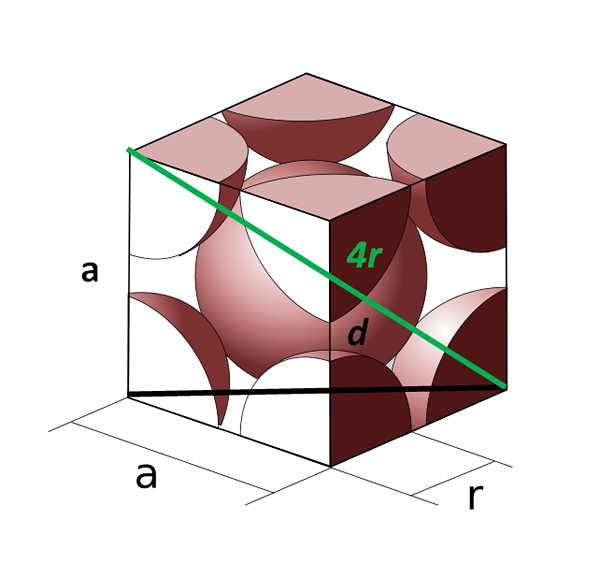Kroppen Unitary Cell sentrerte seg om kroppen. Kilde: COBIQUE_CENTRE_ATOMES_PAR_MAILLE.SVG: Cdang (Original Idea og SVG Execution), Samuel Dupré (3D Odeeling with SolidWorks) Derivatarbeid: Daniele Pugliesi, CC BY-SA 3.0, via Wikimedia Commons

La oss nå se den kubiske cellen sentrert om kroppen. Siden til Det kan ikke lenger være lik 2R, fordi vi har et tomt rom mellom de to atomene i hjørnene. Det er derfor en diagonal d lik 4R (grønn farge) som krysser cellen gjennom midten og berører de motsatte hjørnene, og en annen diagonal d av ansiktet (svart).

Sidene til, d og 4r tegner en rektangel -trekant som vi kan bruke trigonometri for å beregne hva som er verdien av til:

(4r)² = d² + til²

Kan tjene deg: intermolekylære krefter

Men på den annen side, ved basen av enhetscellen, har vi en annen trekant (til, til og d) som vi kan beregne hypotenusen til:

d²  = a² + til²

= 2a²

Erstatning da vil vi ha:

(4r)² = (2²) + a²

(4r)² = 3a²

A = (4/√3) r

V_{Unitary Cell} er lik:

V_{Unitary Cell} = a³

= ((4/√3) R)³

Bestemmelse av emballasjefaktoren

Merk at vi har 1 atom i denne cellen med hensyn til antall atomer i denne cellen, og følger det samme fradraget for den enkle kubiske cellen, og et annet ekstra atom som ligger i midten av cellen. Dermed er det totalt 2 atomer for hver kubikkcelle sentrert på kroppen.

Emballasjefaktoren er da:

Stygg = (2) (4/3) πr³ / ((4/ √3) r)³

= (√3/8) π ≈ 68%

Det vil si at i en kubikkcelle fokusert på kroppen, er 68% av glassvolumet okkupert av atomer. Følgelig er dette krystallinske arrangementet mer kompakt (eller tett) enn den enkle kubikk.

Kubikk sentrert på ansikter

Bestemmelse av cellevolumet

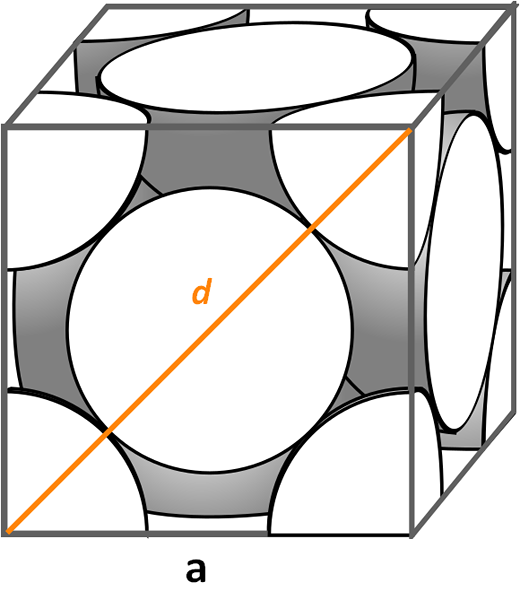Kubisk enhetlig celle sentrert om ansikter. Kilde: Cdang, CC BY-SA 3.0, via Wikimedia Commons

La oss se på den kubiske enhetlige cellen sentrert om ansikter, veldig vanlig i symfiner av uorganiske salter og noen metaller, for eksempel gull og sølv. For å bestemme emballasjefaktoren, må vi starte, etter de tidligere eksemplene, for å finne hva volumet av enhetscellen er. Det er nødvendig å beregne siden igjen til Og så volumet av kuben til³.

Denne gangen er prosedyren enklere og mer direkte, fordi vi har en diagonal d Foran det, sammen med sidene til, De danner en høyre trekant som vi kan bruke trigonometri til:

d² = a² + til²

= 2a²

Lysning til vi vil ha:

til = D/√2

Men vi merker visuelt det d Det er lik 4R, så vi gjør en erstatning:

til = 4r/√2

= 2r 2^1-1/2

= (2√2) r

Å være v_{Unitary Cell} lik:

til³ = ((2√2) R)³

= (16√2) r³

Når det. Derfor er antallet atomer lik:

Nº -atomer = 1/8 (8) + 1/2 (6) = 1 + 3 = 4

Bestemmelse av emballasjefaktoren

Å ha det er det 4 atomer i hver kubikkcelle fokusert på ansikter, og også volumet, som er lik (16√2) r³, Vi kan deretter beregne emballasjefaktoren:

Ugly = (Nº Atoms) (atomvolum)/ (enhetscellevolum)

= (4) (4/3) πr³ / (16√2) r³

Det kan tjene deg: Acilo Group: Struktur, egenskaper, forbindelser og derivater

= π/(3√2) ≈ 74%

Merk at denne cellen er enda mer kompakt enn de forrige: 74% av det totale volumet av cellen er okkupert av atomer. I en perfekt og ren krystall vil dette være ekvivalent med å si at 26% av volumet er tilgjengelig for å være vertskap for andre gjesteatomer.

Kompakt sekskantet

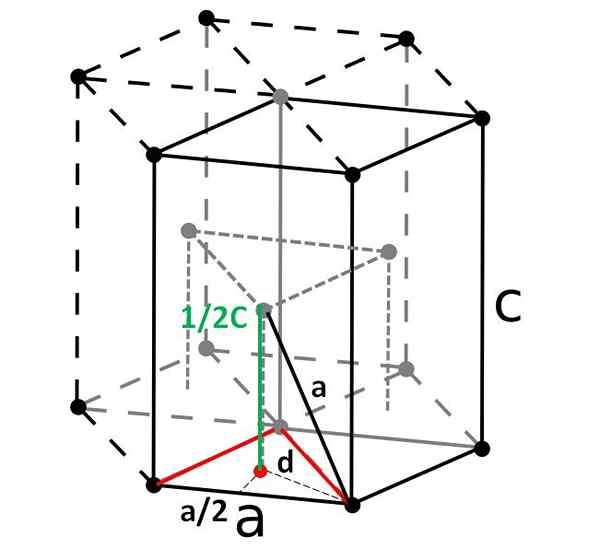Kompakt sekskantet celle og dens rhombohedral primitive celle. Kilde: Original: DornelfVector: Depiep, CC BY-SA 3.0, via Wikimedia Commons

Til slutt, blant de enkleste og mest kompakte enhetscellene har vi den kompakte sekskantede. I motsetning til de forrige, er beregningen av volumet litt mer tungvint. Som det kan sees, er den ikke kubikk, så den har to parametere til og c, Sistnevnte er høyden på cellen.

Bestemmelse av høyden på cellen

Den sekskantede cellen kan deles opp i tre rhomboyan -celler, og fra en av dem vil den bli beregnet til og c. Siden til, Selv om det ikke er så tydelig på bildet over, er det lik 2R. Å beregne c, I stedet bruker vi trekanten og det røde punktproduktet til det interne trekantede prisme av samme celle.

Vi må beregne avstanden d Å kunne bestemme hvor mye det er verdt c. På gulvet er den røde trekanten like, med en vinkel på 60º. Men hvis en annen intern rektangel -trekant blir vurdert med sider til/2 og d, og en vinkel på 30 º (halv), deretter ved trigonometri kan vi bestemme d:

Cos (30º) = (til/2) / d

d = til/√3

Og nå vurderer vi den rette trekanten som er sammensatt av sidene c/2 (grønn), til (svart) og d (prikket):

til² = (til/√3)² + (C/2)²

Lysning c Vi ville ha:

c = √ (8/3) til

Og erstatte til Av 2r:

c = √ (8/3) (2R)

= √ (4 · 2/3) (2R)

= 4√ (2/3) r

Bestemmelse av cellevolumet

For å bestemme volumet av den sekskantede cellen må du multiplisere sekskantområdet med høyden. Å vite at likestillende trekanter har sider til, Høyden beregnes h. Dermed å finne området til en trekant, som er for dette tilfellet √3/4til², Vi multipliserer denne verdien med 6 for å oppnå sekskantområdet: 3 (√3/2)til²

Volumet er derfor:

V_{Unitary Cell} = Sekskantområde x høyde

= 3 (√3/2)til² X 4√ (2/3) r

Og erstatte nok en gang til Av 2r:

V_{Unitary Cell}  = 3 (√3/2) (2R)² X 4√ (2/3) r

= 24√2 r³

Bestemmelse av emballasjefaktoren

I den sekskantede cellen er det 12 atomer i hjørnene, som har 1/6 av volumene deres inne. Det er også 3 indre atomer hvis volum er komplette, og ytterligere 2 atomer på øvre og nedre ansikter hvis halvparten av volumene er inne i cellen.

Derfor er antallet atomer lik:

Nº Atom = 1/6 (12) + 1 (3) + 1/2 (2) = 6 atomer

Og emballasjefaktoren er endelig:

Ugly = (Nº Atoms) (atomvolum)/ (enhetscellevolum)

= (6) (4/3) πr³ / 24√2 r³

= π/(3√2) ≈ 74%

Legg merke til at romfaktoren for den sekskantede cellen er den samme som for kubikkcellen sentrert på ansiktene. Det vil si at begge er like kompakte.

Referanser

1. C. Barry Carter & m. Grant Norton. (2007). Keramisk materialvitenskap og ingeniørfag. Springer.
2. Shiver & Atkins. (2008). Uorganisk kjemi. (Fjerde utgave). Mc Graw Hill.
3. Whitten, Davis, Peck & Stanley. (2008). Kjemi. (8. utg.). Cengage Learning.
4. Wikipedia. (2021). Atomisk pakningsfaktor. Hentet fra: i.Wikipedia.org
5. Brandon. (2021). Hva er Atomic Packing Factor (og hvordan du beregner den for SC, BCC, FCC og HCP)? Materials Science & Engineering Student. Gjenopprettet fra: msestudent.com