Factoring

Hva er faktoriseringen?

Faktorisering er en metode som et polynom uttrykkes i form av multiplikasjon av faktorer, som kan være tall, bokstaver eller begge deler. For å faktorere er faktorene som er felles for begrepene gruppert, og på denne måten blir polynomet dekomponert i flere polynomer.

Når faktorene formidler med hverandre, er resultatet det opprinnelige polynomet. Faktorisering er en veldig nyttig metode når det er algebraiske uttrykk, fordi det kan bli multiplikasjon av flere enkle begreper; For eksempel: 2² + 2AB = 2A _* (A + B).

Det er tilfeller der et polynom ikke kan faktoriseres fordi det ikke er noen felles faktor blant vilkårene; Dermed er disse algebraiske uttrykkene bare delbare mellom seg selv og med 1. For eksempel: x + y + z.

I et algebraisk uttrykk er den vanlige faktoren den maksimale vanlige divisoren for begrepene som utgjør det.

Faktoriseringsmetoder

Det er flere faktoriseringsmetoder, som brukes avhengig av saken. Noen av disse er følgende:

Vanlig faktorisering

I denne metoden blir de faktorene som er vanlige identifisert; det vil si de som gjentas i uttrykkens vilkår. Deretter blir distribusjonseiendommen brukt, den maksimale vanlige divisoren fjernes og faktoriseringen er fullført.

Med andre ord blir den vanlige faktoren til uttrykket identifisert, og hvert begrep er delt mellom dette; De resulterende vilkårene vil bli multiplisert med den maksimale vanlige divisoren for å uttrykke faktoriseringen.

Eksempel 1

Faktoriser (b²x) + (b²og).

Løsning

Først er den vanlige faktoren for hvert begrep, som i dette tilfellet er B², Og så er begrepene delt mellom den vanlige faktoren som følger:

(b²x) / b² = x

(b²y) / b² = y.

Faktorisering uttrykkes, multipliserer den vanlige faktoren med de resulterende vilkårene:

(b²x) + (b²y) = b² (x + y).

Eksempel 2

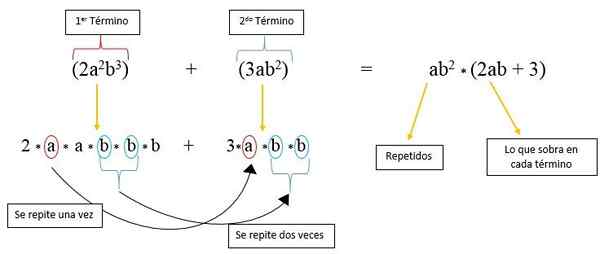
Faktoriser (2. plass²b³) + (3AB²).

Løsning

I dette tilfellet har vi to faktorer som gjentas i hvert begrep som er "A" og "B", og som blir hevet til en makt. For å faktorere dem først, er de to begrepene brutt ned i sin lange form:

2_*til_*til_*b_*b_*B + 3A_*b_*b

Det kan sees at "A" -faktoren bare gjentas en gang i andre periode, og "B" -faktoren gjentas to ganger i dette; Så i den første termen er det bare 2, en faktor "A" og en "B"; Mens i andre periode bare 3 gjenstår bare.

Derfor er det skrevet så mange ganger som "A" og "B" blir gjentatt og multiplisert med faktorene som er til overs fra hvert begrep, som observert i bildet:

Gruppering av faktorisering

Som ikke i alle tilfeller er den maksimale vanlige delingen av et polynom tydelig uttrykt, er det nødvendig å gjøre andre trinn for å kunne omskrive polynom og dermed faktorisere.

Kan tjene deg: koniske seksjoner: Typer, applikasjoner, eksempler

Et av disse trinnene er å gruppere vilkårene for polynom i flere grupper, og deretter bruke den vanlige faktormetoden.

Eksempel 1

Faktoriser AC + BC + AD + BD.

Løsning

Det er 4 faktorer der to er vanlige: i den første termen er det "C" og i det andre er det "D". På den måten er de to begrepene gruppert og separate:

(AC + BC) + (AD + BD).

Det er nå mulig å anvende den vanlige faktormetoden, dele hvert begrep med dens vanlige faktor og deretter multiplisere den vanlige faktoren med de resulterende begrepene, som dette:

(AC + BC) / C = A + B

(AD + BD) / D = A + B

C (A + B) + D (A + B).

Nå oppnås en binomial som er vanlig for begge vilkårene. Å faktorere det multipliseres med de gjenværende faktorene; På den måten må du:

AC + BC + AD + BD =  (C + D) _* (A + B).

Inspeksjonsfaktorisering

Denne metoden brukes til å faktorere kvadratiske polynomer, også kalt trinomials; det vil si de som er strukturert som øks² ± BX + C, der verdien av “A” er forskjellig fra 1. Denne metoden brukes også når trinomialen har X -formen² ± bx + c og verdien av "a" = 1.

Eksempel 1

Faktor x² + 5x + 6.

Løsning

Du har en kvadratisk trinomial av x -skjemaet² ± BX + C. For først. Disse tallene er 2 og 3:

2 _* 3 = 6

2 + 3 = 5.

På denne måten er uttrykket forenklet som følger:

(x² + 2x) + (3x + 6)

Hvert begrep er faktor:

• For (x² + 2x) Det vanlige uttrykket fjernes: x (x + 2)
• For (3x + 6) = 3 (x + 2)

Dermed gjenstår uttrykket:

x (x +2) +3 (x +2).

Ettersom du har en vanlig binomial, for å redusere uttrykket, multipliserer det dette med rester av vilkår, og det må:

x² + 5x + 6 = (x + 2) _* (x + 3).

Eksempel 2

Faktoriser 4A² + 12A +9 = 0.

Løsning

Du har en kvadratisk trinomial av øksformen² ± bx + c og for å faktorere det multipliserer alt uttrykket med koeffisienten til x²; I dette tilfellet, 4.

4. plass² + 12A +9 = 0

4. plass² (4) + 12a (4) + 9 (4) = 0 (4)

16 a² + 12a (4) + 36 = 0

4² til² + 12a (4) + 36 = 0

Nå må to tall bli funnet at når de multipliseres med hverandre, resulterer i verdien av "C" (som er 36) og at når du går sammen i koeffisienten til begrepet “A”, som er 6.

6 _* 6 = 36

6 + 6 = 12.

På den måten blir uttrykket skrevet om, under hensyntagen til at 4² til² = 4a _* 4. plass. Derfor brukes distribusjonseiendom på hvert begrep:

Kan servere deg: Mackinder Box

(4a + 6) _* (4a + 6).

Til slutt er uttrykket delt med koeffisienten til a²; det vil si 4:

(4a + 6) _* (4a + 6) / 4 = ((4a + 6) / 2) _* ((4a + 6)/ 2).

Uttrykket er som følger:

4. plass² + 12A +9 = (2A +3) _* (2a + 3).

Faktorisering med bemerkelsesverdige produkter

Det er tilfeller der det blir en veldig lang prosess for å faktorere polynomene med de tidligere metodene.

Det er grunnen til at et uttrykk kan utvikles med formlene for bemerkelsesverdige produkter, og dermed blir prosessen enklere. Blant de mest brukte bemerkelsesverdige produktene er:

• Forskjell på to firkanter: (a² - b²) = (a - b) _* (A + B)
• Perfekt firkant av en sum: a² + 2ab +b² = (a + b)²
• Perfekt firkant av forskjell: a² - 2ab + b² = (a - b)²
• Forskjell på to terninger: a³ - b³ = (A-B)_*(til² + ab + b²)
• Sum av to terninger: a³ - b³ = (a + b) _* (til² - ab + b²)

Eksempel 1

Faktoriser (5² - x²)

Løsning

I dette tilfellet er det en forskjell på to firkanter; Derfor brukes formelen til det bemerkelsesverdige produktet:

(til² - b²) = (a - b) _* (A + B)

(5² - x²) = (5 - x) _* (5 + x)

Eksempel 2

Faktoriser 16x² + 40x + 25²

Løsning

I dette tilfellet er det et perfekt kvadrat for en sum, fordi to kvadratmeter kan identifiseres, og begrepet til overs er resultatet av å multiplisere to med kvadratroten av den første termen, med kvadratroten av den andre termen.

til² + 2ab +b² = (a + b)²

For å faktorere er det bare de firkantede røttene til første og tredje periode beregnes:

√ (16x²) = 4x

√ (25²) = 5.

Deretter blir de to resulterende begrepene uttrykt atskilt med tegnet på operasjonen, og alt det firkantede polynomet er forhøyet:

16x² + 40x + 25² = (4x + 5)².

Eksempel 3

Faktoriser 27a³ - b³

Løsning

Uttrykket representerer en subtraksjon der to faktorer er forhøyet til kuben. For å faktorere dem, brukes formelen til det bemerkelsesverdige produktet av forskjellen i terninger, som er:

til³ - b³ = (A-B)_*(til² + ab + b²)

For å faktor fjernes den kubiske roten således fra hver sikt av binomialen og multipliseres med kvadratet av den første termen, pluss produktet fra den første med den andre termen, pluss den andre termen kvadrat.

27a³ - b³

³√ (27a³) = 3a

³√ (-b³) = -B

27a³ - b³ = (3a - b) _* [(3a)² + 3AB + b²)]

27a³ - b³ = (3a - b) _* (9a² + 3AB + b²)

Faktorisering med Ruffini -regelen

Denne metoden brukes når du har et polynom av grad større enn to, for å forenkle uttrykket til flere mindre polynomer.

Eksempel 1

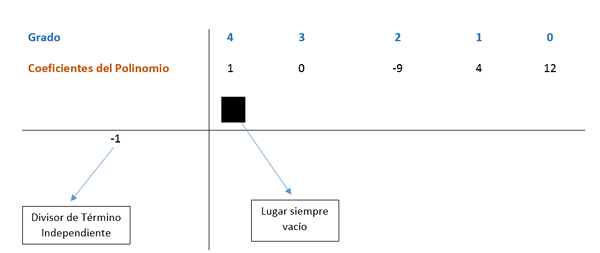
Factorice q (x) = x⁴ - 9x² + 4x + 12

Løsning

Først blir tallene som er divisorer på 12 søkt, som er det uavhengige begrepet; Disse er ± 1, ± 2, ± 3, ± 4, ± 6 og ± 12.

Kan tjene deg: Multipler av 2: Hva er og forklaring

Deretter erstattes X av disse verdiene, fra minst til størst, og slik bestemmes den av de av verdiene divisjonen vil være nøyaktig; det vil si at resten må være 0:

x = -1

Q (-1) = (-1)⁴ - 9 (-1)² + 4 (-1) + 12 = 0.

x = 1

Q (1) = 1⁴ - 9 (1)² + 4 (1) + 12 = 8 ≠ 0.

x = 2

Q (2) = 2⁴ - 9 (2)² + 4 (2) + 12 = 0.

Og så videre for hver divisor. I dette tilfellet er faktorene som er funnet for x = -1 og x = 2.

Ruffini -metoden brukes nå, hvor ekspresjonskoeffisientene vil bli delt på faktorene som er funnet slik at inndelingen er nøyaktig. Polynomiske begrep er bestilt fra større til lavere eksponent; I tilfelle at et begrep mangler med graden som følger i sekvensen, er en 0 plassert på plass.

Koeffisientene er lokalisert i et opplegg sett i følgende bilde.

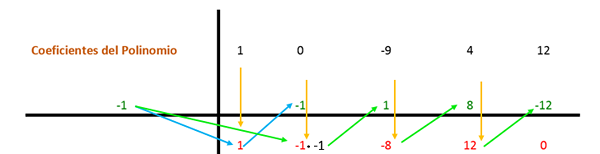
Den første koeffisienten senkes og multipliseres med divisoren. I dette tilfellet er den første divisoren -1, og resultatet plasseres i følgende kolonne. Deretter tilsettes verdien av koeffisienten med det oppnådde resultatet vertikalt, og resultatet plasseres nedenfor. På den måten gjentas prosessen til forrige kolonne.

Da gjentas den samme prosedyren igjen, men med den andre divisoren (som er 2) fordi uttrykket fremdeles kan forenkles.

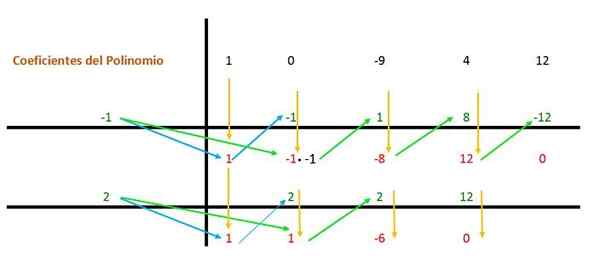
For hver rot vil polynomet ha et begrep (x - a), der “a” er verdien av roten:

(x - (-1)) _* (x - 2) = (x + 1) _* (x - 2)

På den annen side bør disse begrepene multipliseres med resten som gjensto av Ruffini 1: 1 og -6 -regelen, som er faktorer som representerer en grad. På denne måten er uttrykket former: (x² + X - 6).

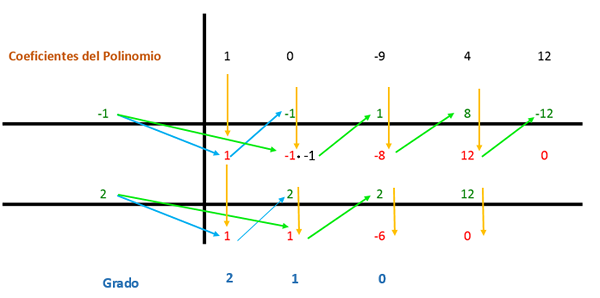
Å oppnå resultatet av polynomfaktorisering ved Ruffinis metode er:

x⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2) _* (x² + X - 6)

Til slutt kan polynom i grad 2 som vises i det forrige uttrykket omskrives som (x+3) (x-2). Derfor er den endelige faktoriseringen:

x⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2)_*(x+3)_*(X-2).

Referanser

1. Arthur Goodman, L. H. (nitten nittiseks). Algebra og trigonometri med analytisk geometri. Pearson Education.
2. J, v. (2014). Hvordan lære barna om å ta et polynom.
3. Manuel Morillo, a. S. (s.F.). Grunnleggende matematikk med applikasjoner.
4. Roelse, p. L. (1997). Lineære metoder for polynomfaktorisering over endelige felt: teori og implementeringer. University Essen.
5. Sharpe, d. (1987). Ringer og faktorisering.