Fysisk

Elektrisk feltstrøm

1551
375
Thomas Karlsen

Hva er elektrisk feltstrøm?

Han Elektrisk feltstrøm eller ganske enkelt elektrisk strømning er en skalær mengde proporsjonal med antall elektriske feltlinjer som krysser en overflate. Det er betegnet med kapitalbrevhovedstaden φ (PHI).

Det elektriske feltet "flyter egentlig ikke" slik en vannstrøm gjør, selv om flytelinjene til væsken ligner de fra det elektriske feltet.

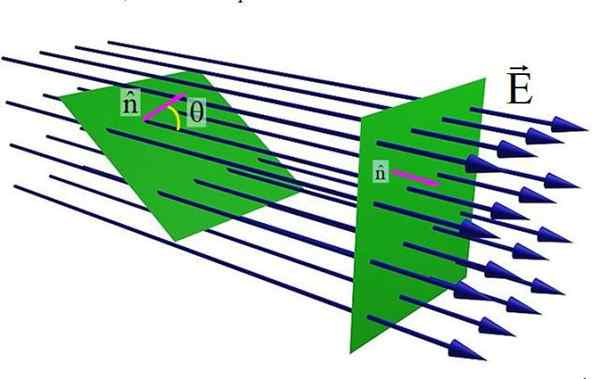
Figur 1. Elektrisk feltstrøm gjennom en flat overflate. Kilde: Wikimedia Commons.

Den øverste figuren viser en flat overflate krysset av et elektrisk felt OG. Når den normale enhetsvektoren til overflaten n og feltet OG De er parallelle, mengden feltlinjer som krysser overflaten er maksimal. Men når vinkelen θ øker mellom n og OG, Antall linjer som føres gjennom den grønne overflaten er lavere.

På den annen side avhenger den elektriske feltstrømmen også av størrelsen på OG, Fordi jo høyere dette, jo flere feltlinjer krysser de overflaten. Og selvfølgelig, desto større er S -området for nevnte overflate, også strømmen, så følgende ligning er etablert:

Φ = e ∙ Sosθ

Dette uttrykket stemmer overens med skalarproduktet blant vektorene OG og n:

Φ = (OG • n) S

Enheten for elektrisk feltstrøm i det internasjonale systemet med enheter hvis n er.m²/C (Newton X Square Metro/Coulomb). Alternativt, ettersom feltet også måles i V/M (Volt på Subway), er den elektriske strømmen i (V ∙ m) m).

Eksempler

I henhold til definisjonen kan den elektriske strømmen være positiv, negativ eller lik 0. Den elektriske feltstrømmen er:

Det kan tjene deg: magnetisering: orbital og spinn magnetisk øyeblikk, eksempler

-Positiv når vinkelen θ mellom OG og n Det er mindre enn 90 º, siden cos θ er større enn null.

-Negativ hvis denne vinkelen er større enn 90 º, for da er cos θ mindre enn null.

-Ugyldig når θ er verdt nøyaktig 90º, fordi cos 90º = 0 og feltlinjene i dette tilfellet er tangentielle for overflaten.

-På den annen side, hvis vinkelen mellom OG og n Det er lik 0, strømmen skaffer seg sin maksimale verdi.

Disse mulighetene vises i følgende bilde:

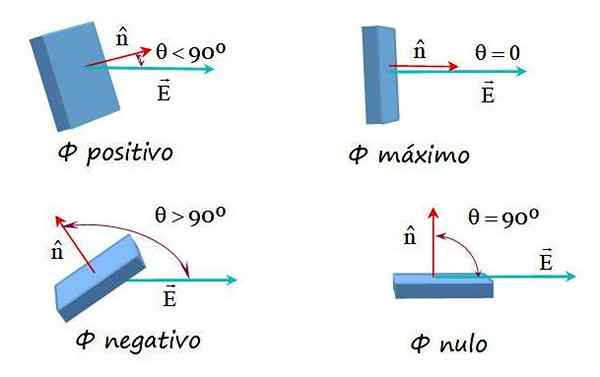Figur 2. Eksempler på elektrisk feltstrøm med forskjellige orienteringer mellom feltet og den normale overflatevektoren. Kilde: f. Zapata.

Elektrisk feltstrøm på en vilkårlig overflate

Tidligere ble den elektriske feltstrømmen bestemt i det spesielle tilfellet av et ensartet felt som påvirker en flat overflate. For en vilkårlig overflate og/eller et ikke -ulik elektrisk felt, vinkelen mellom OG og n kan variere fra punkt til punkt.

I den følgende figuren er det to eksempler, til venstre en buet overflate og til høyre en lukket overflate.

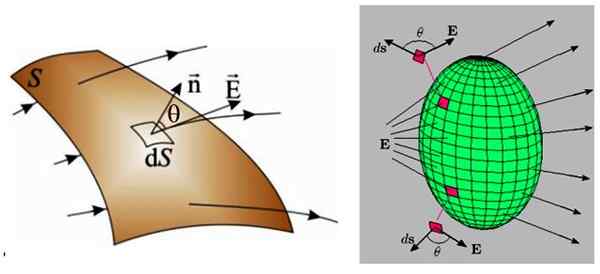Figur 3. Til venstre en vilkårlig overflate som et ikke -ulik elektrisk felt krysser. Til høyre krysser et ikke -ulik elektrisk felt en lukket overflate, derfor er nettostrømmen i så fall ugyldig. Kilde: f. Zapata.

I begge tilfeller er overflaten delt inn i mye mindre regioner, av uendelig størrelse, kalt DS, som den også krysser en uendelig strømning Dφ:

dφ = (OG•n) Ds = (ecosθ) ds

Det totale feltet oppnås ved å legge til alle disse uendelige bidragene:

$\Phi =\int_S^\left (Ecos\theta \right )dS$ Symbolet på S som et abonnement i integralen indikerer at det må beregnes på hele overflaten. Hvis dette er lukket, er det betegnet med en liten sirkel på integralen:

Kan tjene deg: Antoinkonstanter: Formler, ligninger, eksempler

$\Phi =\oint Ecos\theta \: dS$

I tilfelle av lukkede overflater, n Påpek alltid, så strømmen har et skilt + når den er utadvendt, siden vinkelen mellom OG og n er mindre enn 90 º, og tegn - når feltet er innkommende, for da vinkelen mellom OG og n er større enn 90º (se figur 2).

Merk at på den lukkede overflaten til høyre er antall feltlinjer som kommer inn i overflaten lik antall linjer som kommer ut. Derfor er nettostrømmen, definert som den algebraiske summen av den innkommende strømmen og den utgående strømmen, ugyldig.

Den elektriske feltkilden i dette tilfellet er utenfor overflaten, men nettostrømmen vil være forskjellig fra 0 hvis den elektriske feltkilden (fordelingen av belastninger) var inne i overflaten.

Øvelser

Oppgave 1

Du har et elektrisk felt OG = 3.5 kN/C x og en flat rektangulær overflate på 0.35 m bredt med 0.7 m lang. Finn den elektriske feltstrømmen som krysser rektangelet i følgende tilfeller:

a) Overflaten er parallell med flyet YZ.

b) Rektangelet er parallelt med XY -planet.

c) Det normale planet danner en vinkel på 40º med x -aksen og inneholder aksen og.

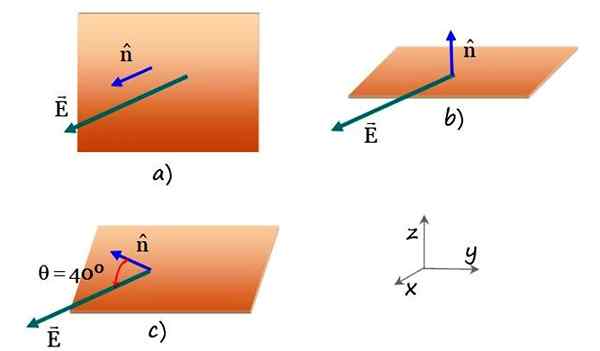Figur 4. Et rektangulært plan krysset av et enhetlig elektrisk felt i forskjellige planorienteringer. Kilde: f. Zapata.

Løsning på

Den normale vektoren og den elektriske feltvektoren er parallell, derfor er vinkelen θ mellom de to 0º og den elektriske strømmen er:

Φ = (e ∙ s) cos 0 = e ∙ s

S -området for rektangelet er:

Kan tjene deg: parallellogrammetode: eksempler, løste øvelser

S = 0.35 m x 0.7 m = 0.245 m²

Erstatning i φ:

Φ = e ∙ s = 3.5 x 10³ N/C × 0.245 m² = 857.5 n ∙ m² /C.

Løsning b

Den elektriske feltstrømmen er 0, siden vektorene OG og n De er vinkelrett på hverandre.

Løsning c

Vinkelen θ mellom feltet OG og den normale vektoren n er 40º (se figur), derfor:

Φ = e ∙ s ∙ cos θ = 3.5 x 10³ N/C × 0.245 m² × cos 40º = 656.9 n ∙ m² /C.

Oppgave 2

Beregn den elektriske feltstrømmen som gir en positiv punktlig belastning som_enten= 2μC som ligger i midten av en radiusfære r = 5 cm.

Løsning

Feltet produsert av belastningen q_enten Den er ikke ensartet, men fra Coulomb -loven er det kjent at den på overflaten av sfæren har en størrelse på:

$E=k\fracq_oR^2$

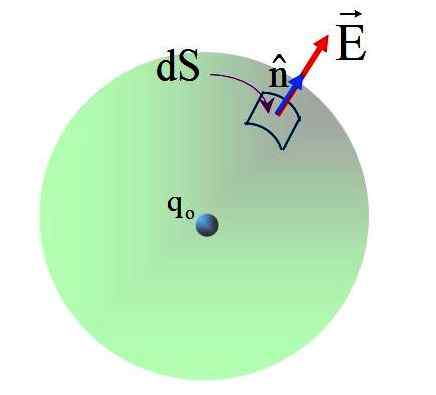Figur 5. Fluer av feltet produsert på overflaten av sfæren med en punktlig belastning i sentrum. Kilde: f. Zapata.

Feltet har radiell retning, og den normale vektoren n, Derfor er vinkelen mellom de to vektorene 0 på alle punktene på den sfæriske overflaten. Erstatte:

$\Phi =\oint Ecos\theta \: dS$

Du må:

$\Phi =\oint k\left (\fracq_oR^2 \right )cos\: 0\times dS=k\left (\fracq_oR^2 \right )\oint dS$

DS er integrert på hele den sfæriske overflaten S er området for det, som er 4πr^2,derfor:

$\Phi =k\left (\fracq_oR^2 \right )4\pi R^2=4\pi q_o$ Som konkluderer med at den elektriske feltstrømmen ikke er avhengig av overflaten, men av belastningen låst i den.

Verdien er:

Φ = 4π × 9 × 10⁹x 2 × 10^-6 N⋅m²/C = 2.3 x 10⁵ N⋅m²/C

Referanser

Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 5. Elektrostatikk. Redigert av Douglas Figueroa (USB).
Giambattista, a. 2010. Fysikk. 2. Ed. McGraw Hill.
Giancoli, d. 2006. Fysikk: Prinsipper med applikasjoner. 6. Ed Prentice Hall.
Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1. Pearson.