Fraksjoner tilsvarer 2/3

De Fraksjoner tilsvarer ⅔ (To tredjedeler leses) er de hvis verdi, uttrykt på en desimal måte, er den samme som oppnås ved å dele 2 med 3: 0.6666 ... Suspensive poeng indikerer at 6 vises uendelige tider i denne divisjonen.

En brøkdel som tilsvarer 2/3 er 4/6 -fraksjonen, da det viser seg at etter å ha løst divisjonen mellom 4 og 6 eksplisitt, desimal 0,6666 .. . Da kan det sies at 4/6 = 2/3 = 0,6666 .. .

Fraksjoner 2/3 og 4/6 er likeverdige fordi ved å dele nummeret til telleren med nevneren, figurer den samme avisen nummer 0.66666 .. . (Kilde: f. Zapata)

En brøkdel, som navnet tilsier, er en del eller en del av enheten. Brøkdelen ⅔ oppnås ved å dele enheten i tre like deler og ta to av disse delene.

Hver brøkdel består av en øvre del, kalt teller, atskilt fra bunnen eller nevner, Gjennom brøkdelinjen. Denominatoren indikerer hvor mange deler enheten er delt, og telleren indikerer hvor mange av disse partene som må tas i betraktning.

Vurder nå 4/6 brøkdelen (les fire sjette). Det er bevist at denne brøkdelen tilsvarer ⅔, siden for å dele enheten i seks deler, må disse trinnene følges:

1. Del enheten i tre like deler.
2. Og del hver av disse delene med halvparten, og oppnår totalt seks like deler.

Hvis 4 deler av 1/6 av enheten er gruppert, er mengden oppnådd en brøkdel av identisk verdi som 2 deler av 1/3 av enheten oppnås. I følgende graf blir den beskrevne prosedyren utført: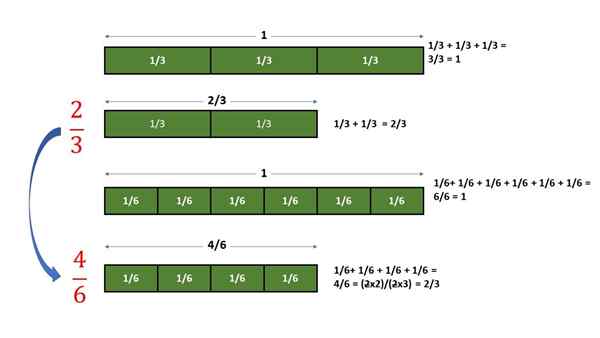

Grafisk bekreftelse av at brøkdel 2/3 tilsvarer brøkdel 4/6. Kilde: f. Zapata.

Kan tjene deg: Numeriske analogier: Typer, applikasjoner og øvelser

Metoder for å finne tilsvarende brøk

Merk at den ekvivalente fraksjon 4/6 kan oppnås fra 2/3 ved å multiplisere med både telleren og nevneren til sistnevnte.

Når du samtidig multipliserer telleren og denominatoren av en brøk med samme antall, oppnås en ekvivalent brøkdel.

En annen måte å finne en brøkdel som tilsvarer en annen, ville være å dele teller og nevner med samme beløp, forutsatt at telleren og denominatoren er nøyaktig delbar med samme tall. Men det er ikke mulig å oppnå, etter splittelse av samme heltall, en tilsvarende brøkdel basert på 2/3, siden nummer 2 og 3 er søskenbarn med hverandre.

Når telleren og nevneren av en brøk er primtall med hverandre, sies det at brøkdelen er irreducible. Og 2/3 -brøkdelen er et godt eksempel på denne typen brøk, faktisk representerer 2/3 settet med alle brøk som tilsvarer 0.666 ..

På den annen side er brøkdel 4/6 reduserbar og tilsvarer brøkdel ⅔, siden numerator 4 og nevner 6 er til og med tall, begge deles med 2.

Så de to måtene å oppnå brøk som tilsvarer en gitt, er:

• Forsterk numerer og nevner samtidig 
• Reduser teller og nevner

Amplifisering av brøk

For å oppnå en brøkdel som tilsvarer en gitt, multipliseres teller og nevner med samme figur. Her er noen eksempler:

Det konkluderes med at ⅔ (to tredjedeler), 4/6 (fire sjette), 6/9 (seks niende) og 8/12 (åtte tolvte) alle er likeverdige brøk med hverandre, men av dem er bare ⅔ ⅔ brøkdel.

Oppsummert, hvis du starter fra den irreducible brøkdelen ⅔, er måten å oppnå noen annen tilsvarende brøkdel å bruke denne formelen:

Kan tjene deg: Løst faktoriseringsøvelser

Med et heltall.

Amplifiseringsmetode for å oppnå ekvivalente fraksjoner. Kilde: f. Zapata

Reduksjon av brøk

Det er en metode som gjør det mulig å oppnå en tilsvarende brøkdel, forutsatt at startfraksjonen har en teller og nevner med en eller mer vanlige deling.

Det er ikke tilfelle av 2/3, som som sagt før, er irreducible. Men for eksempel brøkdel 60/90 (Seksti nittitalls) Det kan reduseres til:

• 6/9, siden både telleren og nevneren er delbar mellom ti.
• 30/45, fordi teller og nevner kan deles mellom to.
• 20/30, siden teller og nevner kan deles mellom tre.
• 12/18, fordi teller og nevner kan deles mellom fem.

Hvis du vil skaffe den irreducible fraksjonen som tilsvarer originalen, er det nødvendig å dele både teller og nevner med sin maksimale vanlige divisor (MCD).

Nedbrytning i faktorer telleren har:

60 = 2² ⋅ 3 ⋅ 5

Og utføre den samme prosedyren i nevneren:

90 = 2 ⋅ 3² ⋅ 5

MCM er de vanlige primefaktorene med sin nedre eksponent, det vil si:

MCM (60; 90) = 2⋅3⋅5 = 30

Deretter er 60 mellom 30 da 2, som er plassert i telleren og ved 90 mellom 30 da 3, 3 plassert i nevneren. Derfor kan den 60/90 irreducible brøkdelen uttrykkes som:

Måter å avgjøre om en gitt brøk tilsvarer 2/3

Den direkte måten å vite om to eller flere brøk er likeverdige, er å uttrykke brøkene direkte på en desimal måte, og hvis alle sifrene sammenfaller, er det sikkert at brøkene er likeverdige. Men det er andre metoder som gjelder 2/3:

Metode 1

Være brøkdel x/y Du vil vite om denne brøkdelen tilsvarer 2/3:

Et avhørtegn er plassert, fordi det ennå ikke er kjent om verdiene til "x" og "y" tilfredsstiller likhet. Å vite det multipliserer i kryss:

Kan tjene deg: proporsjonalitetsrelasjoner: konsept, eksempler og øvelser

3x =? 2 og

Bare når likestilling er oppfylt, er det sikkerhet for at X/Y er en brøkdel som tilsvarer 2/3.

Metode 2

Denne metoden krever å bestemme den maksimale vanlige divisoren (MCD) til telleren og nevneren. Da er begge delt på MCD, og ​​hvis brøkdelen oppnådd etter utført operasjonen beskrevet er 2/3, kan det sies at det er en brøkdel som tilsvarer den.

Eksempler

Eksempel 1

Bestem om fraksjon 40/60 tilsvarer ⅔.

Løsning

Etter metode 1:

Metoden indikerer at den skal multipliseres i kryss:

40 x 3 =? 60 x 2

120 =? 120

Siden likhet er oppfylt, konkluderes det med at 40/60 tilsvarer 2/3.

Eksempel 2

Bestem om brøkdel 120/180 tilsvarer ⅔.

Løsning

I dette eksemplet gjelder metode 2. Den første tingen er å bestemme nedbrytningen i primære faktorer på 120:

120 = 2³ ⋅ 3 ⋅ 5

Og nedbrytningen i nevnerfaktorer er:

180 = 2² ⋅ 3² ⋅ 5

For å bestemme MCD, multipliseres de vanlige faktorene med dens nedre eksponent:

MCD (120; 180) = 2² ⋅ 3 ⋅ 5 = 60

Så:

120 ÷ 60 = 2

180 ÷ 60 = 3

Så det konkluderes med at 120/180 tilsvarer 2/3, det vil si:

Løste øvelser

Oppgave 1

Er brøk 10/15 og 12/18 ekvivalent?

Løsning

Den raskeste måten å bekrefte at det er å formere seg i et kors, siden de ikke er veldig store verdier:

10 x 18 =? 15 x 12

180 =? 180

Det ble oppnådd en likhet, da kan det sies at 10/15 = 12/18.

Oppgave 2

Er brøk 8/12 og 12/20 tilsvarer ⅔?

Løsning

Forenklingsmetoden vil bli brukt, som består av å dele samtidig teller og nevner med vanlige primfaktorer inntil du når et irreducibelt uttrykk:

12/12 = 4/6 = ⅔, det vil si den første brøkdelen tilsvarer ⅔.

For den andre brøkdelen har du:

12/20 = 6/10 = ⅗, men ⅗ er irreducible og forskjellig fra ⅔, derfor tilsvarer ikke den andre brøkdelen ⅔.