Elastisk kraft hva som består, formler og øvelser

De Elastisk kraft Det er kraften som et objekt utøver for å motstå en endring i sin form. Det manifesterer seg i et objekt som har en tendens til å gjenopprette sin form når det er under handling av en deformasjonskraft.

Elastisk kraft kalles også gjenopprettende kraft fordi den motsetter deformasjon for å returnere objekter til likevektsposisjonen. Overføringen av den elastiske kraften er gjennom partiklene som integrerer objektene.

Elastisk styrke på en fjær

For eksempel, når en metallisk fjær er komprimert, blir en kraft som skyver fjærpartiklene utøvd ved å redusere skillet mellom dem, samtidig som partiklene motstår å bli presset på å utøve en kraft i strid med kompresjon.

Hvis den i stedet for å komprimere fjæren blir kastet, strekker seg, er partiklene som integrerer den separert mer. På samme måte motstår partiklene å skille en kraft i strid med å strekke seg.

Gjenstander som har egenskapen til å gjenopprette sin opprinnelige form ved å motsette deformasjonskraft, kalles elastiske objekter. Springene, elastisk gummi og elastiske strenger er eksempler på elastiske gjenstander.

[TOC]

Hva er den elastiske styrken?

Den elastiske kraften (F_k) Det er kraften som et objekt utøver for å gjenvinne sin tilstand av naturlig likevekt ved å ha blitt påvirket av en ytre kraft.

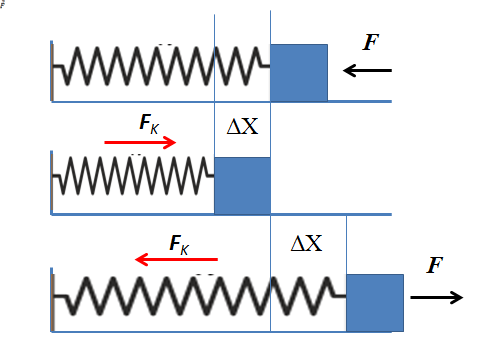
For å analysere den elastiske kraften, vil det ideelle fjærmassesystemet bli tatt med i betraktningen som består av et horisontalt plassert fjær underlagt den ene enden på veggen og i den andre enden til en blokk med foraktelig masse. De andre kreftene som virker på systemet som friksjon eller tyngdekraft vil ikke bli tatt i betraktning.

Det kan tjene deg: Andre likevektstilstand: Forklaring, eksempler, øvelser

Hvis en horisontal kraft utøves på deigen, rettet mot veggen, overføres den til fjæren som komprimerer den. Våren beveger seg fra likevektsposisjonen mot en ny stilling. Ettersom objektet har en tendens til å forbli i balanse, manifesteres den elastiske kraften om våren som motsetter seg den anvendte styrken.

Forskyvningen indikerer hvor mye våren og den elastiske kraften har blitt deformert er proporsjonal med den forskyvningen. Når fjæren er komprimert, øker variasjonen i posisjonen og øker følgelig den elastiske kraften.

Jo mer våren er komprimert, jo mer opposisjonskraft utøver til den når et punkt der den påførte kraften og den elastiske kraften er balansert, og følgelig slutter fjærmassesystemet å bevege seg. Ved å slutte å bruke styrke den eneste kraften som virker er den elastiske styrken. Denne kraften akselererer fjæren i retning i strid med deformasjonen til den gjenvinner likevektens tilstand.

På samme måte oppstår det når du strekker våren og ser på deigen horisontalt. Fjæren er strukket og utøver umiddelbart en kraft som er proporsjonal med forskyvning motstridende strekking.

Formler

Den elastiske kraftformelen kommer til uttrykk i Hooke's lov. Denne loven slår fast at den lineære elastiske kraften utøvd av et objekt er proporsjonal med forskyvning.

F_k = -K.Δs         [1]

F_k = Elastisk kraft

k = Proporsjonalitetskonstant

Δs = Forskyvning

Når objektet beveger seg horisontalt, som i tilfelle av våren underlagt veggen, er forskyvningen Δx, Og uttrykket av Hooke's lov er skrevet:

F_k = -K.Δx        [2]

Kan tjene deg: Konvergent linse: Karakteristikker, typer og trening løst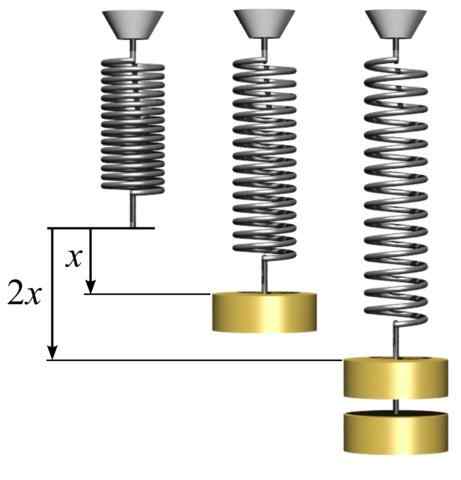Hooke's Law. Elastisk kraft proporsjonal med strekking. [Av SVJO (https: // Commons.Wikimedia.org/wiki/fil: Hookes-lov-Springs.Png)]

Det negative tegnet i ligningen indikerer at vårens elastiske kraft er i motsatt retning av kraften som forårsaket forskyvningen. Proporsjonalitetskonstanten k Det er en konstant som avhenger av hvilken type materiale som våren er utført. Enhetens konstant k er N/m.

Elastiske objekter har en grense for elastisitet som vil avhenge av deformasjonskonstanten. Hvis det strekker seg utover den elastiske grensen, vil den deformere permanent.

Ligning [1] og [2] gjelder små fjærforskyvninger. Når forskyvningene er større, blir vilkårene lagt til med større kraft av Δx.

Kinetisk energi og potensiell energi referert til en elastisk kraft

Den elastiske kraften fungerer på våren ved å bevege den mot likevektsposisjonen. Under denne prosessen øker den potensielle energien i fjærmassesystemet. Den potensielle energien på grunn av arbeidet som er utført av den elastiske kraften, uttrykkes i ligning [3].

U = ½ k .  Δx²[3]

Potensiell energi kommer til uttrykk i Joules (J).

Ved å slutte å bruke deformasjonskraften, akselererer fjæren til likevektsposisjonen ved å redusere potensiell energi og øke kinetisk energi.

Den kinetiske energien til fjærmassesystemet, når likevektsposisjonen når, bestemmes av ligning [4].

OG_k= ½ m.v²[4]

m = masse

v = vårhastighet

For å løse fjærmassesystemet, blir Newtons andre lov anvendt under hensyntagen til at elastisk styrke er en variabel styrke.

Praktiske øvelser av eksempler

Oppnå deformasjonskraft

Hvor mye kraft er nødvendig for å påføre en fjær for å strekke 5 cm hvis fjærkonstanten er 35N/m?

Kan tjene deg: Akselerasjon av tyngdekraften: Hva er det, hvordan den måles og øvelser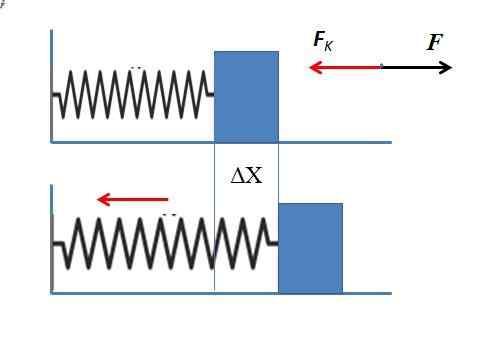Elastisk kraft av en fjær som strekker seg 5 cm

Ettersom anvendelseskraften er imot den elastiske kraften bestemmes F_k Forutsatt at våren er strukket horisontalt. Resultatet krever ikke det negative tegnet siden applikasjonskraften bare er nødvendig.

Hooke's Law

F_k = -K.Δx       

Konstanten k av våren er 35n/m.

Δx = 5cm = 0,05m

F_k = -35n/m . 0,05m

F_k = - 1.75n = - f

Behov for 1,75 n av kraft til å deformere våren 5cm.

Oppnå deformasjonskonstanten

Hva er deformasjonskonstanten på en fjær som strekker seg 20 cm ved handling av en styrke av 60n?

Δx =20cm = 0,2m

F = 60n

F_k = -60n = - f

K = - f_k / Δx

  = -(-60n) /0.2m

K = 300 n/m

Vårkonstanten er 300n/m

Oppnå potensiell energi

Hva er den potensielle energien som er referert til arbeidet som er gjort av den elastiske kraften til en fjær som er komprimert 10cm Og dens deformasjonskonstant er 20n/m?

Δx =10 cm = 0,1 m

K = 20 n/m

F_k = -20n/m . 0,1 m

F_k = -200n

Vårens elastiske kraft er -200n.

Denne styrken fungerer på våren for å bevege den mot likevektsposisjonen. Når du utfører dette arbeidet, øker systemets potensielle energi.

Potensiell energi beregnes med ligning [3]

U = ½ k .  Δx²

U = ½ (20n/m) . (0,1 m)²

U = 0.1Joules

Referanser

1. Kittel, C, Knight, W D og Ruderman, M A. Mekanikk. USA: Mc Graw Hill, 1973, vol. Yo.
2. Rama Reddy, K, Badami, S B og Balasubramanian, V. Oscillamenter og bølger. India: University Press, 1994.
3. Murphy, J. Fysikk: Å forstå egenskapene til materie og energi. New York: Britannica Educational Publishing, 2015.
4. Giordano, n j. College Physics: Resonnement og forhold. Canada: Brooks/Cole, 2009.
5. Walker, J, Halliday, D og Resnick, R. Fundamentals of Physics. USA: Wiley, 2014.