Resulterende kraft hvordan beregnet og løste øvelser

De makt resulterende Det er summen av alle kreftene som virker på samme kropp. Når et legeme eller et objekt er underlagt virkningen av flere krefter samtidig oppstår en effekt. Kreftene som virker kan erstattes av en enkelt kraft som gir samme effekt. Denne unike kraften er den resulterende kraften også kjent som nettokraft og er representert med symbolet F_R .

Effekten den gir F_R Det vil avhenge av størrelsen, retningen og betydningen. De fysiske størrelsene som har retning og mening er vektorstørrelser.

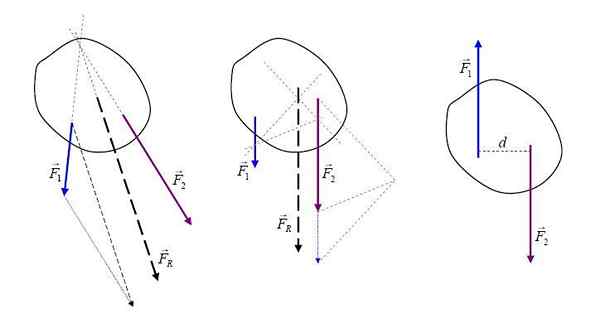Resulterende krefter. Av ilevanat (https: // commons.Wikimedia.org/wiki/fil: rejultanta.JPG), fra Wikimedia Commons

Å være kreftene som virker på et legeme og vektorstørrelser, den resulterende kraften F_R  Det er en vektorsum av alle krefter og kan representeres grafisk med en pil som indikerer dens retning og mening.

Med den resulterende kraften blir problemet med et organ som er berørt av flere krefter forenklet ved å redusere det til en enkelt kraft som virker.

[TOC]

Formel

Den matematiske representasjonen av den resulterende kraften er en sommervektor av kreftene.

 F_R= ∑F          (1)

 ∑F = f₁+ F₂+ F₃+.. F_N           (2)

F_R= Resulterende kraft

∑F = Sum av styrker

N= Antall krefter

Den resulterende kraften kan også være representert med ligningen av Newtons andre lov.

   F_R= m.til          (3)

m= kroppsmasse

a = Kroppsakselerasjon

Hvis ligning (1) erstattes i ligning (3), oppnås følgende ligninger:

∑F = m.til          (4)

F₁+ F₂+ F₃+.. F_{N =} m.til          (5)

Matematiske uttrykk (4) og (5) gir informasjon om kroppsstatus ved å få vektorakselerasjonen til.

Hvordan beregnes den resulterende kraften?

Den resulterende kraften oppnås ved anvendelse av Newtons andre lov som etablerer følgende:

Kan tjene deg: avstandsstyrker

Nettstyrken som virker på et organ er lik produktet av massen ved akselerasjonen som den skaffer seg. (Ligning (3))

Akselerasjonen av kroppen vil ha retning av den påførte nettokraften. Hvis alle kreftene som virker i kroppen er kjent, ville det være nok å legge den vektorisk for å oppnå den resulterende kraften. På samme måte, hvis den resulterende kraften er kjent, vil den deretter dele den av kroppen for å oppnå sin akselerasjon.

Hvis den resulterende kraften er ugyldig, er kroppen i ro eller konstant hastighet. Hvis den resulterende kraften virker på kroppen, er en enkelt styrke lik den kraften F_R=F.

Når flere krefter virker på samme kropp, må vektorkomponentene i styrken tas i betraktning, og hvis disse kreftene er parallelle eller ikke.

For eksempel, hvis vi horisontalt skyver en bok plassert på et bord. Kreftene i horisontal retning er de eneste som gir akselerasjon til kroppen. Den vertikale nettokraften på boka er null.

Hvis den anvendte kraften på boka har en tilbøyelighet med hensyn til det horisontale planet på tabellen, er kraften skrevet basert på de vertikale og horisontale komponentene.

Resulterende av parallelle krefter 

De parallelle kreftene som virker på et legeme er de kreftene som virker i samme retning. De kan være av to typer like forstand eller i motsatt retning.

Når kreftene som virker på et legeme har samme retning og samme forstand eller er i motsatt retning, oppnås den resulterende kraften ved å utføre den algebraiske summen av de numeriske verdiene til kreftene.

Kan tjene deg: elektrisk feltstrømning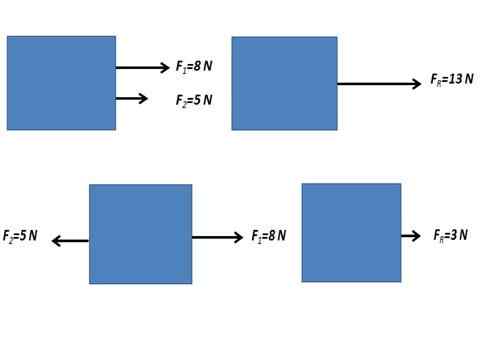Kraft som følge av to parallelle krefter.

Ikke -parallelle krefter

Når ikke -parallelle krefter brukes på et organ, vil de resulterende kreftene ha rektangulære og vertikale komponenter. Det matematiske uttrykket for å beregne nettokraften er:

F_R²= (∑ f_x)²+(∑ f_og)²            (6)

så θ_x= ∑ f_og / ∑ f_x         (7)

∑ f_x  og ∑ f_x= Algebraisk sum av komponentene x og og av anvendte krefter

θ_x= vinkel som danner den resulterende kraften F_R Med aksen x

Merk at kraften som følge av uttrykket (6) ikke blir fremhevet i fet bokstav, og det er fordi den bare uttrykker den numeriske verdien. Adressen bestemmes av vinkelen θ_x.

Uttrykket (6) er gyldig for krefter som virker i samme plan. Når styrkene virker i verdensrommet, blir komponenten tatt i betraktning z av makt hvis du jobber med rektangulære komponenter.

Løste øvelser

1. Bestem kreftene som følge av et legeme som er underlagt følgende krefter vist på bildet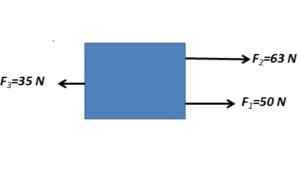

De parallelle kreftene blir lagt til i samme forstand og trekker med den parallelle kraften i motsatt retning

F_R= 63 n + 50 n - 35 n = 78n

Den resulterende kraften har en styrke på 78N med horisontal retning.

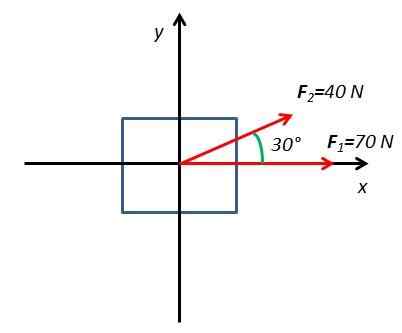
2.Beregn kraften som følge av et legeme under påvirkning av to krefter F_{1 og} F₂. Kraften F₁ Den har en styrke på 70N og blir påført horisontalt. Kraften F₂ Den har en styrke på 40N og blir påført i en vinkel på 30 ° med hensyn til det horisontale planet.

For å løse denne øvelsen trekkes et fritt kroppsdiagram med koordinatakser x og og

Alle komponenter er bestemt x og og av kreftene som virker på kroppen. Kraften F₁ Den har bare en horisontal komponent på aksen x. Kraften F₂ Den har to komponenter F_2x  og f_{2 og} som er oppnådd fra sinus- og kosinusfunksjonene til vinkel 30.

Kan tjene deg: Friksjon: Typer, koeffisient, beregning, øvelser

F_1x = F₁=70n

F_2x = F₂ Cos 30 ° = 40 n.Cos 30 ° = 34,64n

F_1y = 0

F_{2 og}= F₂ uten 30 ° = 40 uten 30 ° = 20n

∑ f_x =70n+34.64n = 104.64n

∑ f_og=20n+0 = 20n

Når de resulterende kreftene på aksen er bestemt x og og Den numeriske verdien av den resulterende kraften oppnås.

F_R²= (∑ f_x)²+(∑ f_og)²

Den resulterende kraften er kvadratroten av sommersummen av styrkene til styrkene

F_R= √ (104.64n)²+(20N)²

F_R= 106,53n

Vinkelen som danner den resulterende kraften F_R Det oppnås fra følgende uttrykk:

θ_x= solbrun^-1(∑ f_og / ∑ f_x)

θ_x= så^-1(20n / 104,64n) = 10,82 °

Den resulterende kraften F_R Den har en styrke på 106,53N og har en retning bestemt av vinkelen på 10,82 ° som dannes med horisontalt.

Referanser

1. Dola, G, Duffy, M og Percival, til. Fysikk. Spania: Heinemann, 2003.
2. Avisison, J h. Fysikkens verden. India: Thomas Nelson and Sons, 1989.
3. Pinsent, m. Fysisk prosess. Storbritannia: Nelson Thomas, 2002.
4. Yadav, S K. Ingeniørmekanikk. Delhi: Discovery Publishing House, 2006.
5. Serway, R A og Jewett, J W. Fysikk for forskere og ingeniører. California, USA: Brooks/Cole, 2010.