Voksende funksjon Hvordan identifisere det, eksempler, øvelser

Du har en Voksende funksjon Når verdien av y øker hvis x også øker, i motsetning til de synkende funksjonene, der verdien av og avtar når x øker.

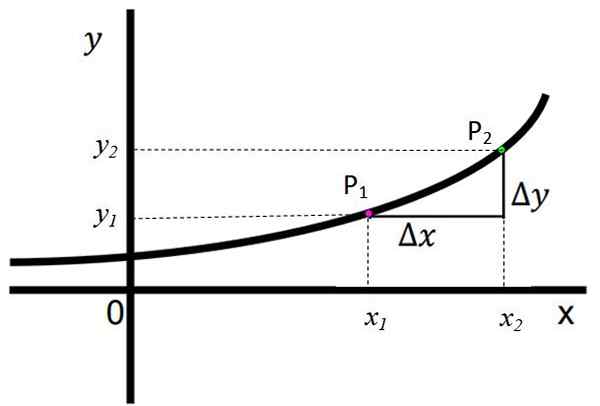
Følgende figur viser en voksende funksjon, og det observeres tydelig at når du går fra venstre til høyre på x -aksen, øker verdien av den respektive koordinaten og tilsvarer f (x) gradvis. Det sies at hvis for alt x₂ > x₁, Da eksisterer det og₂ > og₁.

Figur 1. En voksende funksjon. Kilde: f. Zapata.

Poengene p₁ Og s₂ De vises, de har henholdsvis koordinater (x₁, og₁) og (x₂,og₂). De er definert:

Δy = y₂ -og₁

Δx = x₂ -x₁

I denne funksjonen har både Δy og Δx et positivt tegn, noe som betyr det og₂ > og₁ og x₂ > x₁, henholdsvis. Dette er et klart tegn på at funksjonen effektivt vokser.

Et godt eksempel på alltid voksende funksjon (økende monotont) er den neperiske logaritmen til et reelt tall. Jo høyere antall, jo større er dets logaritme.

[TOC]

Hvordan identifisere en voksende funksjon?

I en enkel og kontinuerlig funksjon som vist i figur 1, er det lett å avgjøre om funksjonen øker eller synker, forutsatt at grafen er tilgjengelig.

Imidlertid kan mer komplekse funksjoner vokse i noen intervaller og redusere andre. Det er derfor vi snakker om Vekstintervaller og reduseres av en funksjon.

I nettverket er det gratis online grafikk, for eksempel Geogebra, som tillater grafering av alle slags funksjoner. Å ha grafen, det er lett å bestemme om funksjonen alltid øker, for eksempel f (x) = log x eller om den har intervaller der den vokser og andre der den avtar og hva som er.

Kriterium for det første derivatet

Tatt i betraktning et visst numerisk intervall I, hvis kvotienten mellom mengder Δy og Δx er positiv, øker funksjonen. Og tvert imot, hvis det er negativt, synker funksjonen.

Det kan tjene deg: Frekvens sannsynlighet: Konsept, hvordan det beregnes og eksempler

Du må:

Δy / Δx> 0 → voksende funksjon

Det faktum at Δy / Δx> 0 og funksjonen øker i et visst intervall, antyder at den første avledet fra funksjonen, eller rettere sagt, kan brukes som et kriterium for å bestemme om faktisk funksjonen vokser i en bestemt intervall eller til og med på et bestemt punkt av domenet ditt.

Faktisk er det første derivatet definert som kurvenes helning hvert punkt:

Noe som betyr at Δx kan gjøres så lite som du vil. Hvis f '(x)> 0 for en viss verdi av x, for eksempel x = a, er kurvenes helning på det tidspunktet f' (a) positiv og funksjonen vil øke der.

Følgende teorem tilbyr et kriterium for å vite når en funksjon vokser i intervallet (a, b):

Teorem

La f (x) være en avledbar funksjon i (a, b). Hvis f '(x)> 0, for enhver verdi av x som tilhører nevnte intervall, sies det at f (x) vokser inn (a, b).

Teoremet brukes for å finne ut i hvilke intervaller funksjonen vokser, etter disse trinnene:

Trinn 1

Finn punktene der f '(x) = 0, så vel som de der f' (x) ikke eksisterer. Disse, kalt Kritiske punkter, Dette er punkter der f '(x) kan endre tegn og derfor f (x) har muligheten til å gå fra å vokse til synkende eller omvendt.

Steg 2

Finn tegnet på F '(x) for vilkårlig verdi i hvert av intervallene som er bestemt av punktene som er funnet i trinn 1.

Trinn 3

Bruk teoremet til å vite om funksjonen vokser eller ikke i hvert intervall.

Eksempler på voksende funksjoner

Det er funksjoner som har noen vekstintervaller og andre av reduksjon, men de som vises nedenfor vokser alltid.

Vekt basert på alder

Vekten av personen siden den ble født, inntil omtrent slutt på ungdomstiden, er nesten alltid en voksende funksjon i alderen. Babyer og barn vokser og utvikler seg gjennom årene, og når de når voksen alder, forventes resten av livet å opprettholde en stabil vekt, selv om oppturene og nedturene er veldig hyppige.

Kan tjene deg: vertikal linje

Logaritmefunksjonen

Funksjonene til reell variabel logaritme Neperian F (x) = ln x og desimal logaritme f (x) = log x vokser alltid.

Kvadratrotfunksjonen til et reelt tall

En annen funksjon som alltid vokser er den firkantede rotfunksjonen til et positivt reelt tall:

y = √x

Den relaterte funksjonen og lineære funksjonen

Den relaterte funksjonen:

f (x) = mx + b

Den vokser når linjen er positiv skråning. Tilsvarende identitet og lineære funksjoner:

f (x) = x og f (x) = øks, med en> 0

De vokser i alt sitt domene.

Eksponentiell funksjon

En eksponentiell funksjon som f (x) = e^x  Og generelt, funksjonen til formen:

f (x) = a^x, Med en> 1

De vokser i alt sitt domene.

Den potensielle IMPAR -indeksfunksjonen

De potensielle funksjonene til merkelig eksponent, som disse:

• f (x) = x³
• g (x) = x⁵

De vokser alltid.

Øvelser

Oppgave 1

Bestem i hvilke intervaller funksjonen som er representert i følgende graf øker:

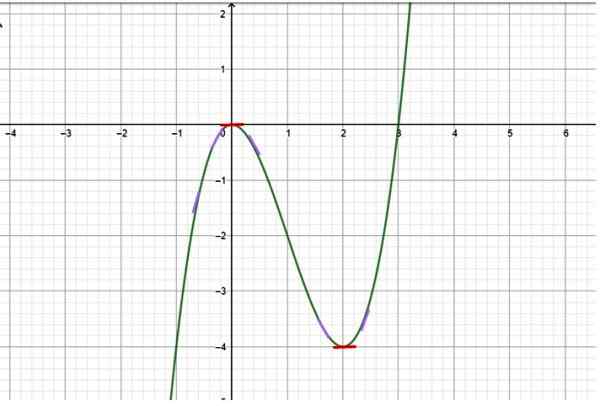Figur 2. Funksjon med vekst og redusere intervaller. Kilde: f. Zapata.

Løsning

Ettersom grafen er tilgjengelig, er det fra den nøye observasjonen bestemt at funksjonen har følgende oppførsel:

-Fra x → -∞ til x = 0 øker funksjonen, siden verdiene til y blir mindre og mindre negative. Små skråningssegmenter er trukket i lilla for å indikere skråningen på tangentlinjen til kurven på forskjellige punkter (skråningen til tangenten til kurven er nettopp den første derivatet).

Disse segmentene har en positiv skråning, så teoremet sikrer at funksjonen vokser i dette intervallet.

-Men ved x = 0 blir kurvenes helning kansellert, noe som er indikert med et lite horisontalt rødt segment. Dette er en kritisk punkt av funksjonen.

Kan tjene deg: hva er matematikk og hva er de for? 7 Viktige applikasjoner

Derfra begynner funksjonen å avta, og bli mer negativ verdiene og. Denne situasjonen fortsetter til x = 2, noe som er et annet kritisk punkt.

Deretter, i intervallet fra x = 0 til x = 2, reduseres funksjonen.

-Fra x = 2 blir funksjonen mindre og mindre negativ, til ved x = 3 krysser x -aksen og fortsetter å bli mer positiv hver gang. Derfor er dette et vekstintervall.

Konklusjon: Vekstintervallene er (-∞, 0) og (2, ∞+), mens reduksjonsintervallet er (0,2).

Oppgave 2

Bestem vekstintervallene for følgende funksjon, gjennom kriteriene til det første derivatet:

f (x) = x² - 2x

Løsning

Etter trinnene som er angitt ovenfor, beregnes det første derivatet og tilsvarer 0 for å finne de kritiske punktene:

f '(x) = 2x -2

2x - 2 = 0

x = 1

Denne verdien bestemmer eksistensen av intervallene (-∞, 1) og (1, ∞+). To vilkårlige verdier er valgt som tilhører hver enkelt:

-For x = 0, som tilhører (-∞, 1), må du f '(0) = 2.0 - 2 = -2. Ettersom resultatet er negativt, synker funksjonen i dette intervallet.

-For x = 3, tilhørende (1, ∞+), er det første derivatet verdt f '(3) = 2.3 - 2 = 4. Siden resultatet er positivt, konkluderes det med at funksjonen vokser i dette intervallet.

Leseren kan tegne den opprinnelige funksjonen f (x) = x² - 2x på en online grafikk for å bekrefte dette resultatet.

Referanser

1. Ayres, f. 2000. Beregning. 5ed. Mc Graw Hill.
2. Leithold, l. 1992. Beregning med analytisk geometri. Harla, s.TIL.
3. Purcell, e. J., Varberg, d., & Rigdon, s. OG. (2007). Beregning. Mexico: Pearson Education.
4. Matemobile. Funksjoner, voksende, synkende og konstant. Gjenopprettet fra: Matemovil.com
5. Requena, b. Voksende funksjoner. Gjenopprettet fra: Universoformulas.com.
6. Stewart, J. 2006. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.