Forskjøvede funksjonskarakteristikker, eksempler, øvelser

De forskjøvet funksjon y = s (x) er en funksjon definert i stykker eller av deler, slik at i et begrenset intervall [a, b] har den et begrenset antall diskontinuiteter, som vi vil kalle x₀ < x₁ < x₂ <… . x_n.  I hvert åpent intervall (x_Yo , x_i+1), og har en konstant verdi av verdien s_Yo, Med diskontinuiteter - -saltos- på punktene x_Yo.

Grafen som er resultatet av en funksjon som denne består av trinn eller trinn. La oss se på et eksempel nedenfor:

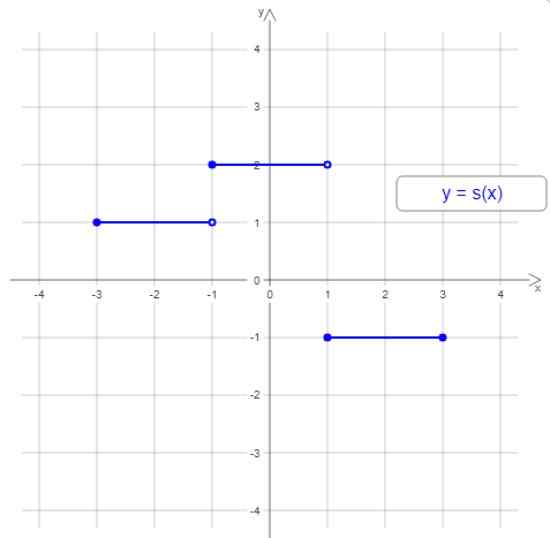
Figur 1. Eksempel på forskjøvet funksjon. Kilde: Wikimedia Commons.

Grafen til denne trappede funksjonen har tre trinn eller forskjøvne intervaller, men generelt kan den forskjøvede funksjonen ha noen trinn. Trinnets bredde kan være annerledes, og trappen er ikke alltid stigende eller synker.

Eksemplets forskjøvet funksjon kan skrives og spesifisere bredden og høye på hvert trinn, slik:

[TOC]

Kjennetegn på den trinnede funksjonen

-Funksjonen mottar navnet med grafen i form av trinn, gitt av segmentene som komponerer det. Hvert segment har en del av funksjonen til funksjonen, og i hver enkelt er funksjonen konstant.

-Domenet til en forskjøvet funksjon er verdiene som tilhører intervallet det er definert for: [a, b], mens området utgjøres av verdiene s_Yo av høyden på trinnene.

I eksemplet på figur 1 er domenet intervallet [-3,3] og området er verdiene -1, 1 og 2.

-Den forskjøvede funksjonen er kontinuerlig bortsett fra i verdiene som avgrenser hvert trinn, punktene x_Yo.

-Escalonada -funksjoner kan legges til og multipliseres for å gi opphav til nye trappemessige funksjoner.

-Derivatet er 0 for punktene der det er definert, siden funksjonen i dem er konstant. For sin del eksisterer ikke derivatet i diskontinuiteter.

-Integralen av den trappede funksjonen s (x) mellom til og b Det eksisterer og tilsvarer summen av områdene til bredden av rektanglene x_Yo- x_I-1 og høyde s_k, lik trinnet.

Kan tjene deg: uavhengige hendelser: demonstrasjon, eksempler, øvelser

Siden området til et rektangel er produktet av basen etter høyde, må vi:

Eksempler på forskjøvne funksjoner

Innenfor de forskjøvne funksjonene er det flere typer, for eksempel funksjonene til Hele delen og funksjonen Enhetlig trinn, så vel som forskjellige forskjøvne funksjoner som beskriver vanlige situasjoner, for eksempel priser for mange tjenester. La oss se på noen eksempler:

- Eksempel 1: Hele partiene

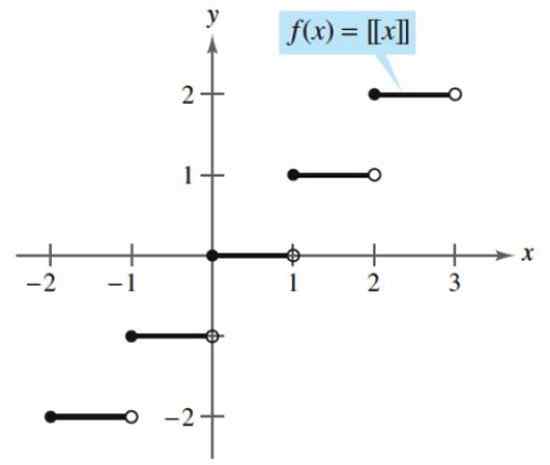
Hele delfunksjonen bruker ofte dobbelt brakett:

f (x) = [[x]]

Og det er definert som en funksjon som tildeler hvert reelt tall det nærmeste eller mindre heltallet, og ignorerer enhver desimal som har tallet. Som tilfellet kan være, har vi:

Tak eller himmelfunksjon

Tildeler hvert domeneverdi det nærmeste heltallet med overskudd. For eksempel:

[[+2.56]] = 3

Desimaldelen som er 0 blir ignorert.56 og det nærmeste heltallet er tildelt som er større enn 2.

Et annet eksempel:

[[-4.2]]= -3

Igjen er desimal del 0 utelatt.2 og det høyeste største heltallet nærmere -4 blir tatt som en verdi av funksjonen, som er -3.

I den følgende figuren er grafen for takfunksjonen, merk at trinnet er avgrenset av en liten hul sirkel til venstre og en full til høyre, siden et hvilket som helst antall av intervallet er det største heltallet tildelt mellom endene mellom ender mellom endene av intervallet.

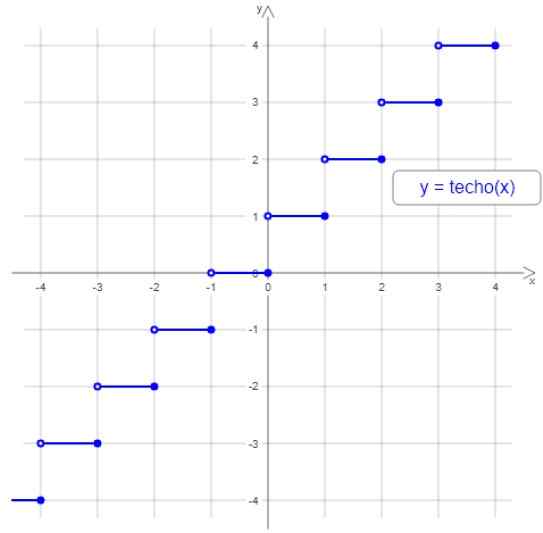Figur 2. Taket eller himmelfunksjonen. Kilde: Wikimedia Commons.

For eksempel er alle verdiene mellom 3 og 4 tildelt hele 4, som er mellom -2 og -1 er tildelt -1 og så videre.

Gulv eller jordfunksjon

Tildeler hvert domeneverdi det nærmeste hele tallet som standard. Eksempler på denne funksjonen er:

Kan tjene deg: Hvor mange tideler er det i en enhet?

[[+3.7]] = 3

[[-1.5]] = -2

[[π]] = 3

Begge funksjonene er kontinuerlige bortsett fra hele tall, der hopp blir presentert, og det er konstant for verdiene mellom heltalene K og K+1.

Figur 3. Gulv eller jordfunksjon. Kilde: Larson, R. Beregning av en variabel.

- Eksempel 2

I en by er drosjeprisen 3.$ 65, for de første 100 m. Og for hver 100 m er 0.$ 18, som er grensen per rute på 50 km.

Det er ønsket å etablere funksjonen som relaterer ruten i meter med kostnadene for tjenesten med $, som må ha dette skjemaet:

f (x) = 3.65 + 0.18. [[x /100]] $

Der hele delfunksjonen kan være av himmelfunksjonen, som basisfrekvensen som er 3 blir lagt til.$ 65. For eksempel, hvis vi vil vite hvor mye det vil bli betalt for en tur på 6.25 km = 6250 m, vil vi ha:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 15.$ 65

Hvis drosjen selskap velger en gulvfunksjon, vil klienten betale litt mindre for turen:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 14.$ 65

Løste øvelser

- Oppgave 1

Langdistanseanrop mellom byer A og B koster 0.40 $ 10 minutter. Etter den perioden er brøkdelen eller ekstra minutt verdt 0.05 $.

Uttrykk kostnadene C (t) for en samtale som varer en viss mengde minutter.

Løsning

Vi kan uttrykke denne funksjonen hvis vi analyserer hva som skjer med hvert alternativ i løpet av en samtale:

For t ≤ 10 minutter

Når T, som er tiden som samtalen varer, er mindre enn eller lik 10 minutter, betales 0.$ 40.

Kan tjene deg: 2 -sifret divisjoner løst

Derfor:

f (t) = 0.$ 40 for T inkludert mellom 0 og 10 minutter.

Vi har allerede en del av funksjonen.

I T> 10 minutter

Entero t case

La oss nå se hva som skjer når tiden for t = 10 minutter overskrides: det kan hende at overskuddet er et heltall, for eksempel at samtalen varer nøyaktig 11, 12, 13, 14 minutter eller mer. I så fall vil mengden av samtalen være:

f (t) = 0.40 + 0.05 (T-10) $, i T større enn 10 minutter, med hele T.

Det vil si at i dette tilfellet: t = 11, 12, 13, 14, 15 ... minutter.

Anta for eksempel at samtalen varer nøyaktig 15 minutter, kostnadene vil være:

f (15) = 0.40 + 0.05 (15-10) $ = 0.$ 65

Desimal sak

Til slutt, vurder saken der samtalen varer en tid med en desimal del. Anta for eksempel at samtalen varer 15 minutter og 45 sekunder, som vil være desimalt 15.75 minutter.

Vi kan uttrykke det i form av hele delen av gulvtypen, forutsatt at selskapet ønsker å gi flere fordeler for klienten eller himmelen:

f (t) = 0.40 + 0.05 ⋅ [[t-9]] $

La oss se hva klienten ville betale hvis det var en gulvfunksjon:

F (15.75) = 0.40 + 0.05 ⋅ [[15.75-9]] $ = 0.40 + 0.05⋅ [[6.75]] $ = 0.40 + 0.05 × 6 $ = 0.70 dollar.

Eller som en himmelfunksjon, i så fall ville kostnadene være:

F (15.75) = 0.40 + 0.05 [[15.75-9]] $ = 0.40 + 0.05⋅ [[6.75]] $ = 0.40 + 0.05 × 7 $ = 0.75 $.

Funksjon og grafisk

Som en funksjon definert av deler er:

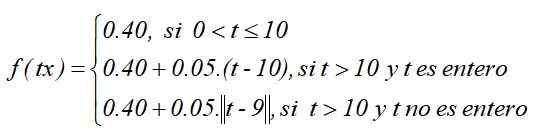
Grafen til funksjonen ville være slik, forutsatt at hele taketypefunksjonen ble valgt:

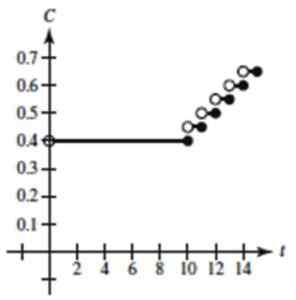Figur 4. Graf over den trinnede funksjonen til øvelsen løst 1. Kilde: Larson, R. Beregning av en variabel.

- Oppgave 2

Beregn integrerte ∫s (x) dx mellom -3 og 3 av den trinnede funksjonen:

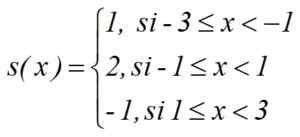
Løsning

Vi bruker definisjonen for integralen av den forskjøvne funksjonen:

Derfor er integralen jeg er:

I = 1. [(-1)-(-3)] + 2.[1- (-1)]+(-1).[3-1] = 2+4-2 = 4

Referanser

1. Jiménez, r. 2006.Matematiske funksjoner. Pearson Education.
2. Larson, r. 2010. Beregning av en variabel. 9na. Utgave. McGraw Hill.
3. Matematikk IV. Funksjoner. Gjenopprettet fra: Cobaqroo.Edu.MX.
4. Wikipedia. Hele delen fungerer. Gjenopprettet fra: er.Wikipedia.org.
5. Wikipedia. Forskjøvet funksjon. Gjenopprettet fra: er.Wikipedia.org.