Eksponentielle funksjonsegenskaper, eksempler, øvelser

De Eksponentiell funksjon Det er en matematisk funksjon av stor betydning for de mange applikasjonene den har. Det er definert som følger:

f (x) = b^x, Med b> 0 og b ≠ 1

Der B er en virkelig konstant alltid positiv og forskjellig fra 1, som er kjent som utgangspunkt. Merk at den virkelige variabelen x finnes i eksponent, På denne måten er f (x) alltid et reelt tall.

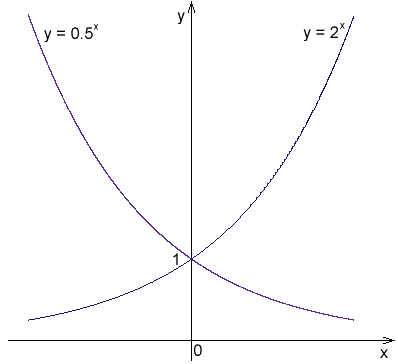Figur 1. Eksponentielle funksjoner med baser 2 og 1/2

Eksempler på eksponentielle funksjoner er følgende:

-f (x) = 2^x

-g (x) = 5⋅e^-3x

-H (x) = 4⋅ (10^2x)

Dette er funksjoner som vokser - eller avtar, i henhold til eksponentens tegn - veldig raskt, så det er snakk om "eksponentiell vekst" når en viss størrelse øker veldig raskt. Dette er grunnen til at de er passende for å modellere veksten av levende vesener, for eksempel bakterier.

En annen veldig interessant anvendelse er den av sammensatt interesse. Jo mer penger du har på en konto, jo flere interesser, og de kan beregne hvert eneste tidsintervall, så små du vil.

Ved hjelp av den logaritmiske funksjonen, som er den omvendte funksjonen til eksponentiell, kan det være kjent etter hvor lang tid en viss kapital øker til en viss verdi.

[TOC]

Eksponentielle funksjonsegenskaper

Figur 2. Eksempler på eksponentielle funksjoner. Kilde: f. Zapata.

Følgende er de generelle egenskapene til enhver eksponentiell funksjon:

-Grafen for en eksponentiell funksjon krysser alltid den vertikale aksen på punktet (0,1), som det kan sees i figur 2. Dette er fordi B⁰ = 1 for enhver B -verdi.

-Den eksponentielle funksjonen krysser ikke hverandre på x -aksen, faktisk er denne aksen en horisontal asymptote for funksjonen.

-Siden b¹ = B, punkt (1, b) tilhører alltid funksjonsgrafikken.

Det kan tjene deg: hepagonal prisme

-Domenet til eksponentiell funksjon er settet med reelle tall og f (x) = b^x Det er kontinuerlig i alt sitt domene.

-Utvalget av eksponentiell funksjon er alle reelle tall større enn 0, noe som også blir lagt merke til med grafikken.

-Den eksponentielle funksjonen er en etter en, det vil si hver x -verdi som tilhører funksjonens domene, har et unikt bilde i ankomstsettet.

-Det inverse av eksponentiell er den logaritmiske funksjonen.

Bestemte egenskaper for eksponentiell funksjon

Som vi har sagt før, kan eksponentiell funksjon øke eller synke.

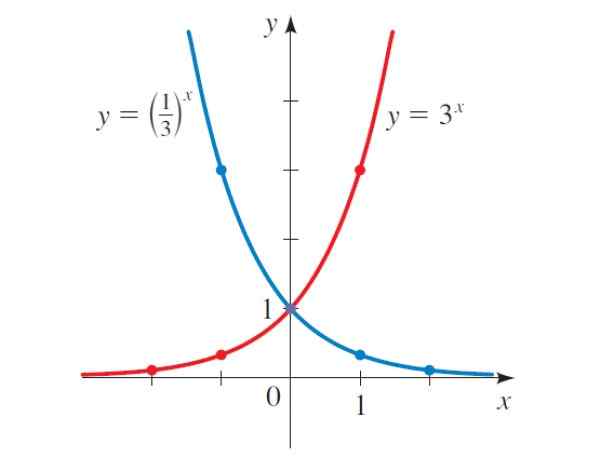
Hvis grafen i figur 2 studeres nøye, bemerkes det at hvis b> 1, vokser funksjonen, for eksempel y = 3^x, Men i tilfelle av y = (1/3)^x, med b < 1, la función decrece.

Vi har to typer eksponentielle funksjoner med følgende spesielle egenskaper:

For b> 1

-Funksjonen vokser alltid.

-Når verdien av B øker, vokser funksjonen raskere, for eksempel y = 10^x vokser raskere enn y = 2^x.

-Når variabelen er større enn 0, skaffer funksjonen verdier større enn 1, det vil si:

For x> 0: y> 1

-Og hvis x<0, entonces f(x) < 1.

For b < 1

-Funksjonen avtar alltid.

-Ved å redusere verdien av B, avtar funksjonen raskere fremdeles. For eksempel y = (1/5)^x avtar raskere enn y = (1/3)^x.

-For verdier på x lavere enn 0, tar funksjonen verdier større enn 1, det vil si:

For x 1

-Til slutt, når x> 0, da og < 1.

Eksempler på eksponentielle funksjoner

Den eksponentielle funksjonen er veldig nyttig for modellering av fenomener i vitenskap og økonomi, som vi vil se nedenfor:

Naturlig eksponentiell funksjon

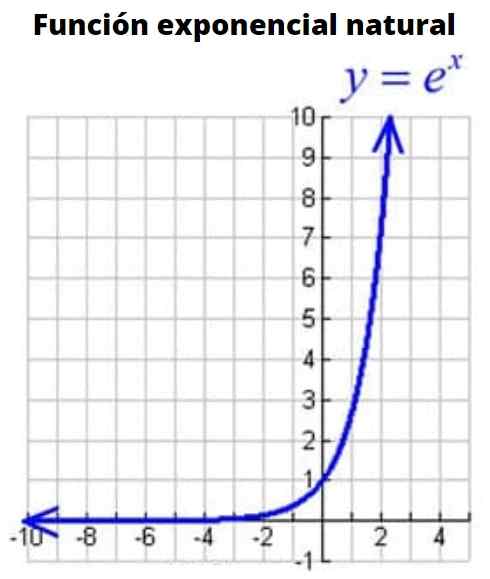Figur 3: Naturlig eksponentiell funksjonsgraf

Det er funksjonen hvis base er tallet E eller Euler -nummer, et irrasjonelt tall hvis verdi er:

Kan tjene deg: Tilleggsvinkler: Hva er, beregning, eksempler, øvelser

E = 2.718181828 ..

Denne basen, selv om det ikke er et rundt nummer, fungerer veldig bra for mange applikasjoner. Derfor regnes det som det viktigste grunnlaget for alle eksponentielle funksjoner. Den naturlige eksponentielle funksjonen kommer til uttrykk på matematisk måte som:

f (x) = e^x

Den eksponentielle funksjonen vises ofte i sannsynlighet og statistikk, siden forskjellige sannsynlighetsfordelinger, for eksempel normalfordeling, Poisson og andre, kan uttrykkes gjennom eksponentielle funksjoner.

Kontinuerlig sammensatt interesse

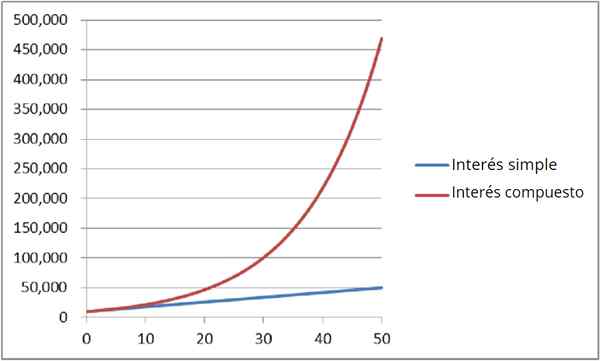Figur 4: Sammenligning av enkel og sammensatt interesse

Det kalles også Kontinuerlig kapitalisering. Å vite hvor mye penger TIL Du har etter t År, eksponentiell uttrykk brukes:

A (t) = p ⋅ e^Rt

Der P er mengden penger som opprinnelig er satt inn, er r renten per år og til slutt t er antall år.

Bakteriets vekst

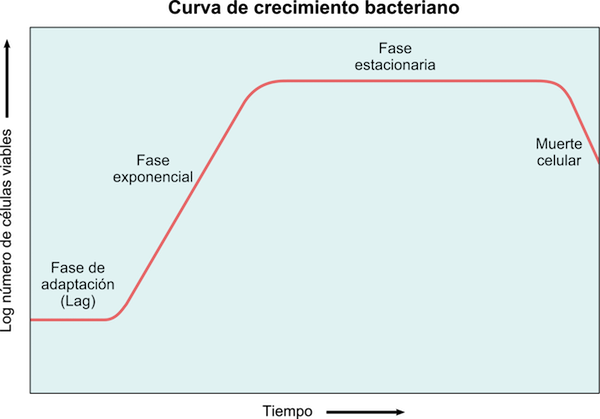Figur 5: Bakteriell vekstkurve der latens, eksponentielle, stasjonære og dødsfaser observeres

Bakterier vokser eksponentielt, slik at vekst kan modelleres av:

N (t) = n_enten ⋅ e ^Kt

Hvor n (t) er den eksisterende befolkningen etter tid t (nesten alltid i timer), n_enten Det er den innledende populasjonen og k er en konstant som avhenger av bakterietypen og forholdene under hvilke næringsstoffer som er tilgjengelige.

Radioaktivt forfall

Enkelte kjerner i naturen er ustabile, så de avviser å forvandle seg til mer stabile, en prosess som kan være veldig kort eller ta tusenvis av år, avhengig av isotop. Under de radioaktive forfallspartiklene sendes ut og noen ganger også fotoner.

Noen radioaktive isotoper har medisinske anvendelser, for eksempel den radioaktive jod I-131, som leger bruker i diagnosen og behandlingen av visse skjoldbruskkjertelforhold.

Radioaktivt forfall er modellert av en eksponentiell funksjon.

Kan tjene deg: Hvor mange tideler er det i en enhet?

Løste øvelser

Ligningene der den ukjente fremstår som eksponent kalles eksponentielle ligninger. For å fjerne verdien av den ukjente, brukes forskjellige algebraiske manipulasjoner og bruken av logaritmefunksjonen, som er den motsatte funksjonen til eksponentiell.

La oss se på noen løste øvelser som illustrerer poenget.

- Oppgave 1

Løs følgende eksponentielle ligninger:

til 5^x = 625

b) 5^x = 2^X-1

Løsning på

Tallet 625 er et multiplum på 5, når vi dekomponerer det, finner vi det:

625 = 5⁴

Derfor kan vi skrive:

5^x = 5⁴

Siden basene er lik både venstre og høyre, kan vi matche eksponentene og få:

x = 4

Løsning b

For denne øvelsen kan vi ikke ty til teknikken som tidligere er brukt, siden basene ikke er de samme. Men vi kan bruke logaritme på begge sider av likhet, på denne måten:

5^x = 2^X-1

Logg (5^x) = log (2^X-1)

Nå brukes følgende egenskap til logaritmene:

Log mⁿ = n⋅log m

Og gjenstår:

x⋅log 5 = (x-1) ⋅log 2

x⋅ (log 5 - log 2) = -log 2

x = - log 2 ÷ (log 5 - log 2)

- Oppgave 2

Angi hvilken funksjon hver av grafene som er vist nedenfor tilsvarer:

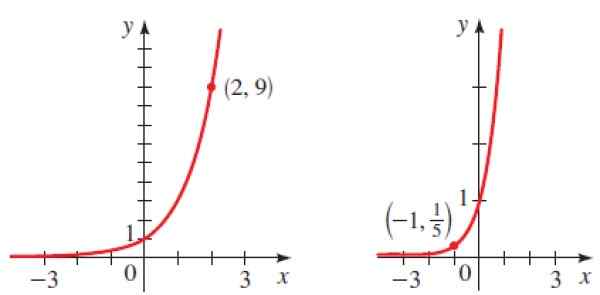Figur 6. Grafikk parast de eksponentielle funksjonene til den løste øvelsen 2. Kilde: Stewart. J. Forkalkning.

Løsning på

Ettersom det er en voksende graf, er B større enn 1 og vi vet at punktet (2.9) tilhører grafen, derfor:

y = b^x → 9 = B²

Vi vet at 3² = 9, derfor b = 3 og funksjonen er y = 3^x

Løsning b

Igjen erstatter vi det gitte punktet (-1, 1/5) ved y = b^x å få:

1/5 = b^-1 = 1/b

Da B = 5 og den etterspurte funksjonen er:

y = 5^x

Referanser

1. Figuera, J. 2000. Matematikk 1. Diversifisert. Co-bo-utgaver.
2. Gid Hoffmann, J. Utvalg av matematikkproblemer for fjerde. År. Ed. Spphinx.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Larson, r. 2010. Beregning av en variabel. 9na. Utgave. McGraw Hill.
5. Stewart, J. 2006. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.