Matematiske funksjoner

En matematisk funksjon er forholdet mellom to størrelser, når den første er avhengig av den andre. Shuttersock

Hva er matematiske funksjoner?

De Matematiske funksjoner De er uttrykket på matematisk språk i et forhold mellom to variabler, og verdien av den første av variablene avhenger av den andre. Normalt er disse variablene symbolisert med bokstavene x og y.  Variabel x kalles domene eller uavhengig variabel; og til y, kodominium eller avhengig variabel.

La oss se på et eksempel. Vi har to variabler eller størrelser: dollar og øre. Vi vet at 100 øre tilsvarer en dollar. Derfor er cent (x) domenet og dollar (y) tilsvarer codominium. Dette forholdet kan uttrykkes med følgende funksjon (F):

F (x) = y / 100

Hvis jeg har 143 øre i sparegrisen min, og jeg vil vite hvor mange dollar jeg har spart, bruker jeg bare funksjonen:

F (x) = 143 /100

Derfor har jeg $ 1,43.

Vi kan også uttrykke det omvendte forholdet, det vil si at en dollar tilsvarer 100 øre. Følgelig investeres kategoriene for variablene: Dollar (X) blir domenet mens cent er Codominium. Vi uttrykker det på denne måten:

F (x) = x x 100

Hvis jeg har $ 1,43 i sparegrisen min, men jeg vil vite hvor mange øre dette tallet er likeverdige, er det nok å bruke denne andre funksjonen.

F (x): 1,43 x 100

Resultatet går tilbake til mine 143 originale øre.

Variablene av matematiske funksjoner

En variabel er ganske enkelt et symbol (x, y, z) som representerer en rekke elementer.

I forrige eksempel symboliserte variablene X og Y dollar og dollar av dollar. Men de samme symbolene (x og y) kan brukes til å representere en uendelig elementer, for eksempel: alder på en person og deres vekt; Antall fly til en viss destinasjon og en periode (per uke, per måned, per år) osv.

Kan tjene deg: syntetisk divisjon

Variablene kan klassifiseres i mange typer, men de mest relevante for matematiske funksjoner er følgende:

• Avhengig variabel: de som har verdi avhenger av verdien som er tilordnet andre variabler i funksjonen.
• Uavhengig variabel: Endringer i denne typen variabel påvirker verdiene til resten av variablene i funksjonen.
• Kvantitativ variabel: Det uttrykkes med definerte numeriske mengder. De kan være hele eller desimale tall.

Kjennetegn på matematiske funksjoner

1- Forholdet mellom variablene er uttrykt i form av ekvivalens.

2- For hver verdi av variabel x er det en, og bare en ekvivalent av variabelen og. Og omvendt: For en viss verdi av y er det en, og bare et resultat av variabel x.

3- De kan være representert grafisk på et kartesisk plan, som gjør det mulig å forutsi oppførselen til en av variablene fra den andre.

4- Den moderne definisjonen av matematisk funksjon skyldes den tyske matematikeren Peter Dirichlet (1805-1859), som publiserte den i 1837.

Typer matematiske funksjoner

Matematiske funksjoner kan klassifiseres i henhold til forskjellige kriterier, for eksempel forholdet som er etablert mellom variablene x og y o den matematiske oppførselen til funksjonen.

Blant hovedtypene er følgende:

Algebraiske funksjoner

De er preget av å etablere et forhold mellom komponenter som kommer til uttrykk enten gjennom et monomiell eller polynom. Dette forholdet kan bestemmes gjennom enkle matematiske operasjoner, for eksempel subtraksjon, multiplikasjon, deling, sum, potensiering eller kringkasting.

Lineære funksjoner

Når de er representert på et kartesisk plan, vises de med formen som en rett linje som kutter koordinataksen på et bestemt punkt. Derav navnet deres, selv om de også er kjent som førstegradsfunksjoner.

Kan tjene deg: Vanlig faktor: Kjennetegn, eksempler, øvelser

Funksjoner i stykker

I denne typen verdien av kodominiet og endrer oppførselen til funksjonen. Det er derfor to intervaller med forskjellig oppførsel i forhold til domeneverdien.

Transcendente funksjoner

De er svært komplekse funksjoner. Vanlige algebraiske operasjoner er ikke nok (subtraksjon, multiplikasjon, deling, sum, potensering eller stråling) for å bestemme forholdet mellom variablene, slik at andre matematiske verktøy må brukes, for eksempel derivater, integraler eller logaritmer.

Trigonometriske funksjoner

Denne typen funksjoner viser det numeriske forholdet som eksisterer mellom de forskjellige elementene i en trekant og andre geometriske figurer, spesielt blant dens vinkler. Formler for bryst, kosinus, tangent, Secant og Harmonte er eksempler på denne typen funksjoner.

Injeksjonsfunksjoner

Funksjonene av denne typen er preget av forholdet mellom forholdet mellom domene og codominium. Til hver av verdiene til sistnevnte tilsvarer bare ett domeneverdi. Det kan også skje at en domeneverdi ikke har noen tilsvarende verdi i codominium.

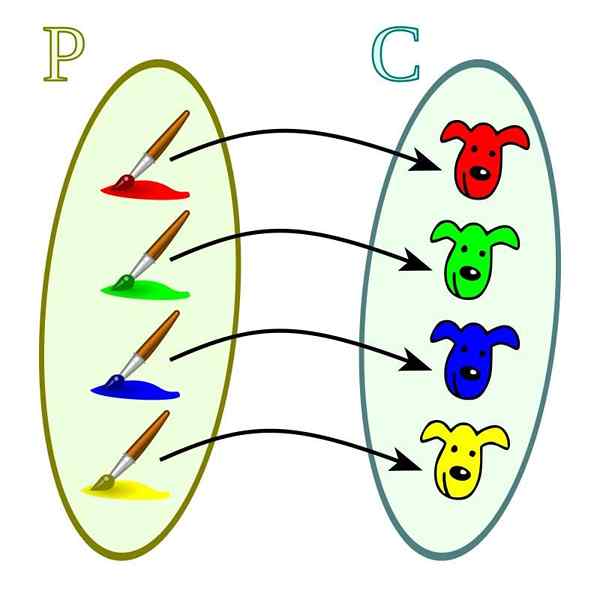Injeksjonsfunksjon. Kilde: Wikimedia Commons

Onjektive funksjoner

I dette tilfellet er hver av størrelsene på kodominiet relatert til minst en av domeneverdiene. De skiller seg fra injeksjonsfunksjonene der kodominiumverdiene kan relateres til mer enn ett av domeneverdiene.

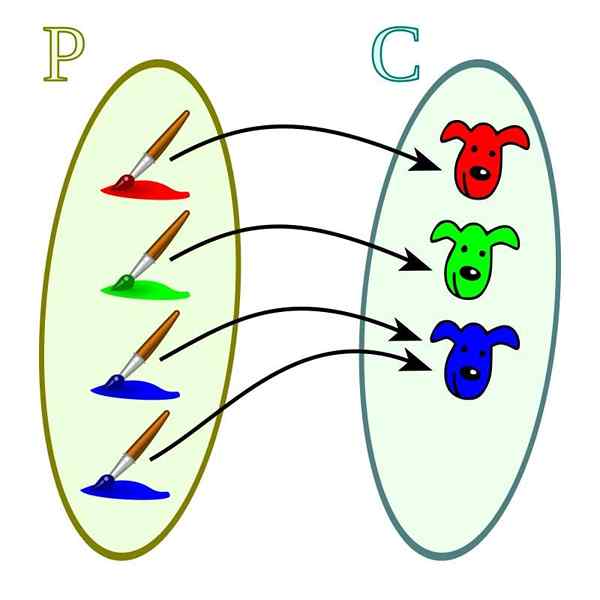OVERIVISJON FUNKSJON. Kilde: Wikimedia Commons

Bijektive funksjoner

Denne typen funksjoner presenterer både injiserende og overvektive egenskaper.

Hva er matematiske funksjoner for?

Funksjonene er mye brukt i alle vitenskaper som har matematikk som hjelpevitenskap. Dette er tilfelle fysikk, ingeniørfag, medisin, finans, statistikk, blant mange andre.

Kan tjene deg: Frekvensfordeling: Hvordan lage et bord, eksempel, trening

I dagliglivet

Vi kan imidlertid også være nyttige for å løse enklere daglige problemer.

Se for deg at bestefaren din har gitt deg 10 mynter, som du vil bruke på sjokolade. I kiosken har du gitt de 10 myntene til den avhengige, og ber ham om å gi deg alle sjokoladene som kan kjøpes med det mengden valuta. De har gitt deg 5 sjokolader. Hva er prisen på hver?

Vi foreslår problemet: Hvis 5 sjokolader tilsvarer 10 mynter, hvor mange mynter tilsvarer det en enkelt sjokolade?

Vår uavhengige variabel (x) er mengden sjokolade (5), mens den avhengige variabelen (y) tilsvarer antall valutaer, det vil si 10.

Vi uttrykker funksjonen som følger:

F (x) = 2x/x

F (x) = 2 (5)/5

F (x) = 10/5

F (x) = 2

Og vi har allerede svaret: hver sjokolade koster 2 mynter.

Referanser

1. (S/F). Elementære funksjoner. Nettstedet for matematiske funksjoner. Hentet fra undions.Wolfram.com.
2. (S/F). Hva er en funksjon? Hentet fra matematikk.com.