Analytisk geometri

Vi forklarer hva analytisk geometri, dens historie, hvilke studier og applikasjoner er

Hva er analytisk geometri?

De Analytisk geometri Det er grenen av matematikk der geometri og algebra kombineres, for å løse forskjellige geometriske problemer gjennom algebraiske teknikker.

Bruk koordinatsystemer, for eksempel det kartesiske koordinatsystemet, som skylder navnet René Descartes. På denne måten er det mulig å knytte kurver i flyet og i verdensrommet, med algebraiske ligninger.

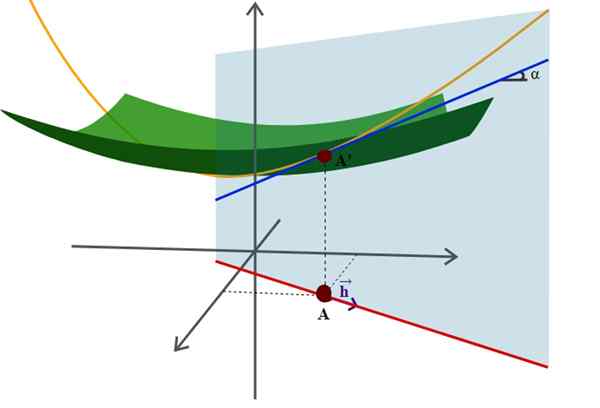
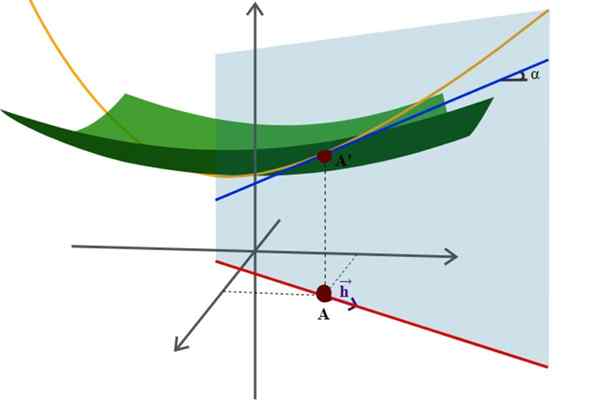Diagram over en overflate i rommet og dens retningsderivat, en av de mange mer avanserte anvendelsene av analytisk geometri. Kilde: Wikimedia Commons.

Et eksempel på dette er den velkjente ligningen av radius r -riortion sentrert om opprinnelsen til koordinatsystemet:

Utvilsomt er det i mange tilfeller enklere å jobbe med det algebraiske uttrykket av en kurve, enn med dens geometriske representasjon i seg selv. Dette er tilfelle når du beregner kryss mellom kurver, eller finner tangens- eller tørkelinjer til dem.

Tilsvarende gjennom analytisk geometri er det mulig å layoutfunksjoner grafikk. Og som kjent, tillater funksjonene modellering av vitenskap og ingeniørproblemer. Derfor er analytisk geometri til stede i læreplanene til karrieren knyttet til disse kunnskapsområdene.

Kort historie med analytisk geometri

Analytisk geometri har sin opprinnelse i første halvdel av 1600-tallet, i hånden til to bemerkelsesverdige franske matematikere: René Descartes (1596-1650) og Pierre de Fermat (1601-1665).

Rene Descartes

Imidlertid kan det sies at bakgrunnen hans går tilbake til århundrer, til den greske matematikeren Apollonius av Pergamo (262-190 A.C.). Han skrev en avhandling om konikkene, som han ga navnene deres til: Omkrets, ellipse, lignelse og hyperbola.

Det kan tjene deg: sammensatt proporsjonalitet: forklaring, tre sammensatte regel, øvelser

Dermed var Apollonios arbeid grunnlaget for, mye senere, den franske René Descartes og Pierre de Fermat la grunnlaget for analytisk geometri, uavhengig. Men Descartes regnes som faren til denne vitenskapen, ettersom han var den første som ga ut sine verk.

Descartes, Fermat og Euler

I talen til 1637 -metoden forenet Descartes to fagområder som inntil da hadde blitt skilt: algebra og geometri. I sitt arbeid introduserer Descartes det kartesiske koordinatsystemet, for å lokalisere punkter i flyet og i verdensrommet.

Den benytter seg også av andre grads algebraiske ligninger med to variabler, for å beskrive de koniske seksjonene og er dedikert til å løse geometriske problemer med dem. Også for å skape en god del av den matematiske notasjonen som for øyeblikket brukes.

Pierre de Fermat er mer assosiert med optikk enn med analytisk geometri, men deres bidrag er imidlertid bemerkelsesverdige.

I 1629 gjenopptok Fermat konikkene til Apollonius av Pergamo og skapte teknikkene som utgjør den analytiske geometrien, oppfant sitt eget koordinatsystem og tydelig definere nøkkelbegrepet for Geometrisk sted, som studiet av analytisk geometri begynner.

Fermats verk så imidlertid ikke lyset før i 1679, utgitt av sønnen, da matematikeren allerede hadde dødd. Av denne grunn tilskrives farskapet til analytisk geometri Descartes.

Deretter til de franske matematikerne etablerte den sveitsiske Leonardo Euler (1707-1783) de formelle basene for analytisk geometri. Euler introduserte flere koordinatsystemer i planet og rommet: rektangulære, polare og skrå koordinater, samt transformasjoner fra ett system til et annet.

Kan tjene deg: Hvordan er informasjonen innhentet i en undersøkelse?

I sine verk om analytisk geometri utdypet Euler også klassifiseringen av forskjellige kurver, i henhold til graden av den representative algebraiske ligningen (tredje og fjerde orden) og studerte dens egenskaper intensivt, ligningene til tangentene, krumningene, symmetriene og mye mer.

Hva studerer analytisk geometri?

Stort sett fokuserer analytisk geometri på studiet av geometriske elementer, for eksempel punkter, segmenter, linjer, kurver, overflater og volumer. For å gjøre dette, som nevnt ovenfor, etablerer det algebraiske ligninger som beskriver og relaterer disse elementene, og lar deres ledelse gjennom algebraiske teknikker.

Hovedmålene med analytisk geometri, på en veldig sammendrag, er følgende:

1. Etablere det kartesiske koordinatsystemet og det polare koordinatsystemet, for å lokalisere punkter i flyet, så vel som utvidelsen til punkter i rommet.
2. Tegn segmenter, rette, kurver og overflater på det kartesiske planet og rommet.
3. Utlede ligningene som analytisk beskriver en kurve og konstruksjonen av den på flyet og/eller rommet, samt studiet av alle dens egenskaper.
4. Klassifiser kurver, overflater og volumer.
5. Utled grunnleggende formler for å løse problemer på bemerkelsesverdige punkter, rette, planer, vinkler, parallellisme, vinkelrett, avstander, kryss, områder og mer.
6. Løs geometriske problemer gjennom anvendelse av algebraiske metoder, for hvilke formler som refererer til bemerkelsesverdige punkter, ligninger for linje, planer, vinkler, avstand mellom punkter, mellom linjer og punkter, tangenspunkter, tørre linjer, områder, områder og mye mer.
7. Arbeid med vektorrom og produkter mellom vektorer.

Avstand mellom to punkter

Som et eksempel på de mange anvendelsene av analytisk geometri, er en av de enkleste beregningen av avstanden mellom to punkter i flyet. Er to punkter P₁ Og s₂, av koordinater (x₁,og₁) og (x₂,og₂) henholdsvis avstanden D mellom dem beregnes av:

Kan tjene deg: trinomial

Polare koordinater

Et planpunkt kan spesifiseres gjennom sin "r" avstand til opprinnelsen til koordinatsystemet, kalt polo, og vinkelen som danner linjen som inneholder punkt og stolpe, med den horisontale aksen eller polaraksen.

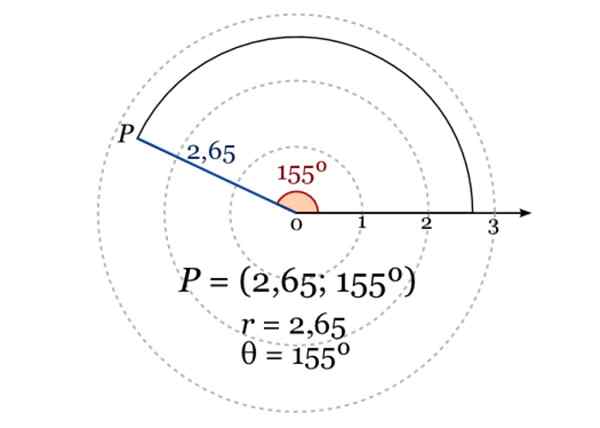Bildet viser de polare koordinatene til et punkt P, der r = 2.65 og vinkelen i grader med hensyn til polaraksen er 155º. Kilde: Wikimedia Commons.

Analytiske geometri -applikasjoner

Grunnlaget for uendelig beregning

Analytisk geometri er avgjørende for utvikling av uendelig beregning, siden den letter den grafiske representasjonen av kurver og funksjoner, og jobber med dem på en analytisk måte, for å lage modeller som representerer fenomener av naturen.

Kart

Det kartesiske koordinatsystemet hjelper til med å lage kart og identifisere steder gjennom breddegrad og lengde, tilsvarer de kartesiske koordinatene til et punkt i flyet.

Topografiske beregninger

Ulike typer koordinatsystemer brukes i topografi og utgjør grunnlaget for deres studie og applikasjoner. Blant dem er det polare koordinatsystemet beskrevet ovenfor.

Celestial Bodies -baner

De koniske seksjonene, beskrevet gjennom analytisk geometri, deltar i viktige naturfenomener, for eksempel banen til himmellegemer, underlagt tyngdekraften. For eksempel beskriver planetene og noen kometer elliptiske baner rundt solen, med dette som ligger i et av søkelysene.

Sivil arkitektur og konstruksjoner

Tallrike kurver er en del av de arkitektoniske konstruksjonene, for eksempel kan kablene til en hengende bro ta form av lignelser.

Globale posisjoneringssystemer

Det globale posisjoneringssystemet eller GPS gjør mulige steder med presisjon, samt bevegelige gjenstander, for eksempel kjøretøy og båter. Det hjelper også folk å komme seg lettere til sine destinasjoner, og veileder dem på de beste rutene.