Heptagon

Et eksempel på heptagon

Hva er en heptagon?

Han Heptagon Det er en polygon med syv sider og syv indre vinkler. Som et geometrisk ord stammer ordet heptagon fra det greske Hepta, som betyr syv, og gonos, oversatt som en vinkel. Det er derfor en polygon med syv vinkler.

En polygon er en flat geometrisk figur som danner og lukker tre eller flere segmenter, også kalt sider. De vanlige punktene som sidene har kalles Hjørner.

Regionen mellom tilstøtende sider, på innsiden av figuren, er Indre vinkel, hvis toppunkt også er en av toppunktene til heptagon.

Hvis alle sider og indre vinkler har samme mål, er det en Regelmessig heptagon, Ellers er en uregelmessig heptagon. Uregelmessige heptoner tar i bruk et stort utvalg av former.

En heptagon kan også være konveks enten konkav, I henhold til målet på dens indre vinkler. Hvis de indre vinklene måler mindre enn 180 °, er heptagon konveks, men hvis en eller flere av nevnte vinkler overstiger 180 °, er det konkav.

En heptagon hvis sider er det samme tiltaket kalles Balateral. Dette kan være konkav eller konveks, regelmessig eller uregelmessig.

Regelmessig og uregelmessig heptagon

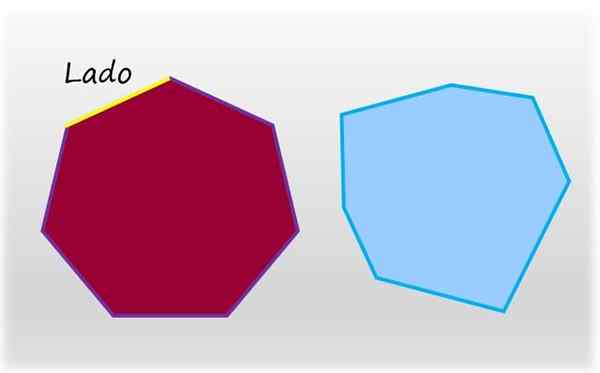Heptagon er den flate og lukkede figuren på syv sider. Til venstre, en vanlig heptagon, hvis sider og indre vinkler har like store mål. Til høyre, en uregelmessig heptagon. Kilde: f. Zapata.

Den vanlige heptagon er en som har sine syv sider og dens syv indre vinkler med like mål, det motsatte av en uregelmessig heptagon, som har minst en side av forskjellige mål, eller en annen indre vinkel.

Den vanlige heptagon

Symmetri

En vanlig heptagon er en svært symmetrisk figur. Det kan trekkes segmenter som forbinder et toppunkt med midtpunktet på motsatt side, som alle krysser hverandre i sentrum av heptagon. Dette er de syv symmetriaksene i figuren.

Kan tjene deg: Område for en vanlig og uregelmessig Pentagon: Hvordan det tas, øvelser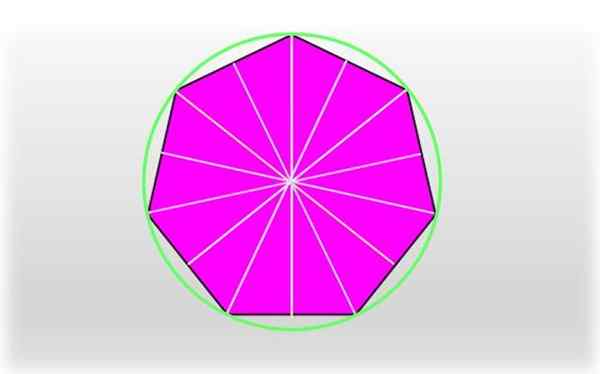 En vanlig heptagon og dens symmetriakser. Omkretsen som passerer gjennom hver av toppunktene til heptagon kalles omskrevet omkrets.

Segmentet som blir med i et toppunkt med sentrum av heptagon kalles Circunradio, Det tilsvarer radien til den unike omkretsen som passerer gjennom hver eneste av toppunktene, som vist på figuren.

Vinkler

I heptagon skiller følgende vinkler seg:

• Indre vinkel ϕ, hvis toppunkt sammenfaller med en av toppunktene til heptagon, som er sidene av vinkelen, to av de tilstøtende sidene av heptagon. For en vanlig heptagon er målet på hver av de syv indre vinklene omtrent 128.57 °.
• Ekstern vinkel, Den som dannes mellom en av sidene og forlengelsen av en av de tilstøtende sidene, og er den vanlige toppunktet mellom disse to sidene. På samme måte dannes syv ytre vinkler og verdien deres beregnes ved å trekke 180 ° fra den indre vinkelen, som for den vanlige heptagon resulterer i 51.43 °.
• Sentral vinkel θ, Den har toppunktet i sentrum av den vanlige Heptgon. Det beregnes ved å dele 360 ​​° med 7, noe som resulterer i omtrentlig 51.43 °.

Summen av den indre vinkelen og den sentrale vinkelen er lik 180 °, det vil si:

ϕ + θ = π

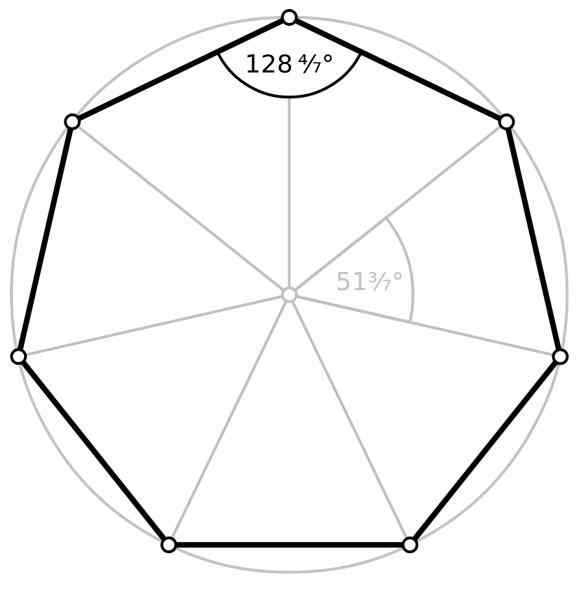Indre vinkel og sentral vinkel på den vanlige heptagon. Kilde: Wikimedia Commons

Område

For den vanlige heptagon er det formler, mens du for den uregelmessige heptagon må ty til andre metoder, for eksempel å dele den i andre enklere polygoner, for eksempel trekanter.

Det kan tjene deg: Regel T: Karakteristikker, slik at det er eksempler

Regelmessig heptagon -område

1. Hvis omkretsen p og apotemen til_p:

Være det for heptagon -området. Det er en formel for å beregne området, gyldig for vanlig polygon:

2. Hvis L og Apothem er kjent til_p:

Siden omkretsen er summen av sidene, og siden måler L i den vanlige heptagon, oppnås den:

P = 7⋅L

Erstatte i forrige formel:

3. Hvis siden er kjent        

Følgende er en omtrentlig, gyldig formel når målet på heptagon er kjent:

A = 3.634 ∙ l²

Uregelmessig heptagon -område

Det uregelmessige heptagon -området kan beregnes med triangulering, som består av å dele heptagon i fem trekanter (se følgende figur). Området for hver beregnes og resultatene blir lagt til, og oppnår dermed det komplette området av heptagon.

Den andre metoden kalles Gauss Determinant, Og det er nødvendig å plassere heptagon i et rektangulært koordinatsystem, for å kjenne koordinatene til hvert toppunkt. Området beregnes med en formel som involverer verdiene til disse koordinatene.

Diagonaler

De Diagonaler De er segmenter som forbinder et toppunkt med et annet som ikke er påfølgende (hvis segmentet kobler sammen to påfølgende vertikaler er side). En heptagon har 14 diagonaler totalt.

Antall diagonaler d av en hvilken som helst polygon, beregnes gjennom formelen:

D = n · (n - 3) / 2

Erstatter n = 7, gjenstår:

D = 7 · (7 - 3) / 2 = 7 · (4/2) = 14

Sum av interne vinkler

For enhver heptagon, uavhengig av om den er regelmessig eller ikke, er summen av de indre vinklene lik 900 ° eller 5π radianer.

Det kan tjene deg: trigonometriske grunner: eksempler, øvelser og applikasjoner

Denne egenskapen er veldig enkel å demonstrere, for dette er heptagon delt inn i individuelle trekanter som ikke overlapper hverandre, og tegner rettlinjede segmenter som forener toppunktene, uten å krysse hverandre.

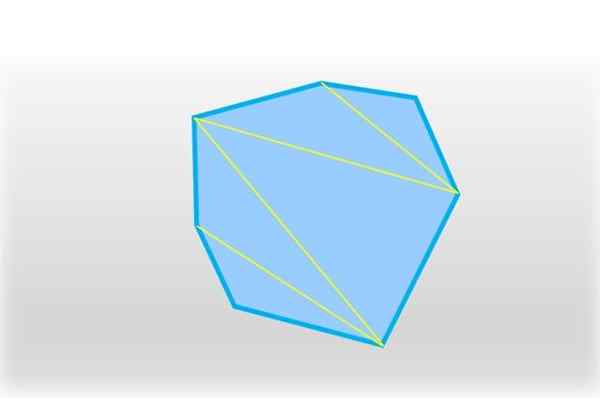En heptagon kan deles inn i fem trekanter, sammenføyning av et segment to ikke -samlet oppholdsmenn. Kilde: f. Zapata.

Fem trekanter oppnås, og i hver enkelt er summen av dens indre vinkler 180 °, som multiplisert med 5 er lik 900 °:

5 x 180 ° = 900 °

Formler

Omkrets

For en vanlig heptagon fra L, beregnes omkretsen P som følger:

P = 7⋅L

Hvis omkretsen er uregelmessig, blir lengdene på hver av de syv sidene lagt til.

Intern vinkelmål

I en vanlig heptagon måler den indre vinkelen θ:

θ = [180 (n-2)]/n

Hvor n = 7.

Apothem

Være l siden av den vanlige heptagon. Apothem er segmentet som går fra sentrum av heptagon, vinkelrett mot motsatt side.

La a_p Lengden på apotemen. Å kjenne radien til den omskrevne omkretsen, som er betegnet som r_c Og L -siden av heptagon, har du:

Når du kjenner den indre vinkelen θ, tilsvarer ovennevnte:

Område

Hvis det er en vanlig heptagon fra L, blir området A gitt av:

A = 3.634 ∙ l²

Når heptagon er uregelmessig, er de rektangulære koordinatene til hvert toppunkt nødvendig, gitt av (x_n , og_n), Hvor n = 1, 2, 3 ... 7.

Deretter brukes følgende formel for å finne område A:

Diagonaler

Antallet Diagonaler er gitt av:

D = n · (n - 3) / 2

Hvor n = 7 for heptagon.

Hvordan lage en heptagon

Følgende animasjon viser hvordan du tegner omtrent en vanlig heptagon, ved hjelp av regel og kompass.

Bygging av den vanlige heptagon. Kilde: Wikimedia Commons

Referanser

1. Alexander, d. 2013. Geometri. 5. plass. Utgave. Cengage Learning.
2. Lemonis, m. Vanlig hepalle kalkulator. Gjenopprettet fra: Calcresource.com.
3. Matematikk åpen referanse. Polygonområde. Gjenopprettet fra: Mathpenref.com.
4. Universformler. Heptagon. Gjenopprettet fra: Universoformulas.com.
5. Wikipedia. Heptagon. Gjenopprettet fra: er.Wikipedia.com.